小3算数「式と計算(□を使って場面を式に表そう)」指導アイデア《□を用いて式を立てる》
執筆/神奈川県横浜市立庄戸小学校教諭・渡邊督之
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時(本時)式に表すすべての数が分かっている文章から未知数を設定し、□を用いて式を立てる。
▼
第2時 さまざまな場面を、□を用いた場合や用いない場合の減法や乗法の式に表す。
▼
第3時 前時に表した式を基に問題をつくり、□を用いると的確に具体的な場面を表現できることに気付く。
▼
第4時 まとめ
本時のねらい
□を用いて式を立て、その根拠を図を使って説明することができるとともに、問題場面通りに数量の関係を立式できるよさに気付くことができる。
評価規準
□を用いて式を立て、図を使って説明することができる。問題場面通りに数量の関係を立式できるよさに気付いている。
本時の展開

あめを18こもっています。20こもらいました。あめは全部で38こになりました。
さぁ、今日はみんなでこの問題を考えましょう。
え? 何を考えるのか分かりません。
いつもの問題と同じですよね。
いつもは分からないところがあるけど、今日はありません。
答えが分かっています。
どんな問題だったらよいのですか。
「全部で何個になりますか」だったらいいと思います。
「38個」が分からなかったら、考えられます。
では、「38」を隠しますね。そう言えば、二年生のときは分からないところをどう表していましたか。
□にしていました。
□にすると、「あめを18こ持っています。20こもらいました。あめは全部で□こになりました」になりますね。式はどうなりますか。
18+20です。
□もあるから、18+20=□でもいいよ。
どうしてたし算になるのか、説明できますか。
はじめに持っていた数と、もらった数が分かっているからです。
図にすると、分かります。
図にするといいんですか。では、先生が書いていきますね。はじめに持っていたのは18個だから……。
〇〇〇〇〇〇〇〇〇〇〇……
先生! 全部書かなくても、線にしようって前に話していました!

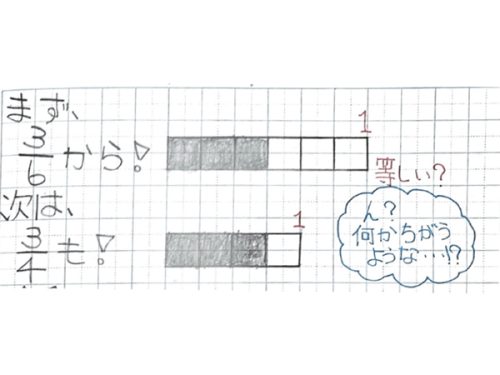
こうすると、「部分」と「部分」が分かってて、「全部」が分かってないから、たし算だって分かります。
この問題で□にできるのは、全部の「38」だけですか。
そうです!
え、そうかな。
はじめの「18」とか、もらった「20」もできるよ。
では、もらった「20」を□にしてみますね。あめを18こもっています。□こもらいました。あめは全部で38こになりました。これも式にできますか。
できます。
さっきのとほとんど変わらないね。
では、もらった数を分からない□にしたこの問題を、式に表してみましょう。なぜそうなるのか、図もかいて説明してくださいね。

□を用いて式を立て、その根拠を図を使って説明することができる。
見通し
「全部」が□のときのやり方で、式が立てられそう。(方法の見通し)
「全部」が□のときの図と同じようにかけば、説明ができそう。(方法の見通し)
「全部」が□のときと同じように、たし算の式で、□の場所が変わりそうね。(結果の見通し)
自力解決の様子
A つまずいている子
「全部」が□のときの式や図を活用して、18+□=38の式を立てたり、図をかいたりすることができていない。
B 素朴に解いている子
18+□=38という式を立てたり、もらった数が□になる図をかいたりしている。
C ねらい通り解いている子
「全部」が□のときの式や図と関連付けながら、18+□=38や38-18=□という式を立てたり、もらった数が□になる図をかいたりしている。
学び合いの計画
本単元では、式には事柄を表現する役割があることを実感できるようにします。それを実感するために、「部分」と「全部」という加減法に必要なすべての情報が分かっている問題を提示し、まずは答えを求めるための立式ではなく、事柄を表現するための立式につながるようにします。
イラスト/横井智美