小6算数「分数と整数のかけ算・わり算」指導アイデア《分数×整数の意味と計算のしかた》
執筆/新潟県新潟市立万代長嶺小学校教諭・清野佳子
監修/文部科学省教科調査官・笠井健一
新潟県新潟市立新津第一小学校校長・間嶋 哲
単元の展開
第1時(本時)(分数)×(整数)の意味と計算のしかたを考える。
▼
第2時 (帯分数)×(整数)の計算のしかたを考える。
▼
第3時 (分数)÷(整数)の意味と計算のしかたを考える。
▼
第4時 (分数)÷(整数)の計算のしかたをまとめ、計算する。
▼
第5時 (分数)÷(整数)の計算について、途中で約分するよさを検討する。
▼
第6時 (帯分数)÷(整数)の計算のしかたを考える。
▼
第7時 (分数)×(整数)と(分数)÷(整数)の計算のしかたをまとめる。
▼
第8時 (分数)×(整数)と(分数)÷(整数)の計算を確かめる。
本時のねらい
1缶で[MATH]\(\frac{4}{7}\)[/MATH]㎡塗ることができるペンキ2缶分で塗れる広さについて、乗法や分数の意味に基づいたり、図を用いて表したりすることを通して、(分数)×(整数)では分子に乗数をかければよいことを説明している。
評価規準
(分数)×(整数)の計算のしかたについて、言葉や図で表すことができる。

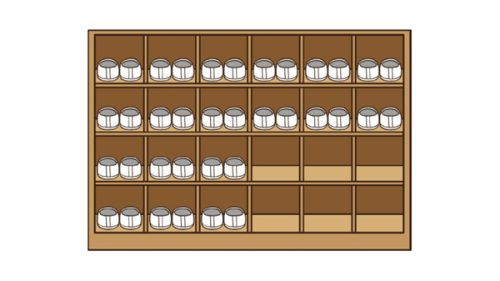
みくさんたちは工作で使うペンキを買いに来ました。ぬる広さは1㎡なのですが、1かんでは足りないようなので、2かん買おうと考えています。
ポイント
1m×1mの実物大の正方形を提示して、塗る広さのイメージをもたせます。さらに、提示した正方形を基に、1㎡の図のかき方を導入しておきます。そして、被乗数が小数の場合を基に、被乗数が分数の場合にも乗法を用いることができることを把握させましょう。
1缶で0.4㎡を塗れるペンキがあります。
じゃあ、2缶買うから0.4×2=0.8で0.8㎡だ。
2缶買っても1㎡には足りないね。
0.4㎡は、1㎡の半分までいかないから2缶買っても足りないよね。
ほかに、1缶で [MATH]\(\frac{4}{7}\)[/MATH]㎡を塗れるペンキがあります。このペンキなら、なん㎡塗れるでしょうか。
[MATH]\(\frac{4}{7}\)[/MATH]㎡なら1㎡の半分を超えているよね。だから2缶買えば足りるはずだよ。
1缶で0.4㎡を塗れるペンキが2缶のときは0.4×2だったから、今度は[MATH]\(\frac{4}{7}\)[/MATH]×2でいいんだよね。
小数のとき、「1缶で塗れる広さ×買う数」にしたから、今は[MATH]\(\frac{4}{7}\)[/MATH]×2でいいと思う。だけど、なん㎡塗れるのかな。

[MATH]\(\frac{4}{7}\)[/MATH]×2は、どのように計算すればいいのかな。
見通し
図を使って考えれば説明できそうだよ。
たし算に直して考えれば説明できそうだよ。
0.4×2を0.1で見ると、4×2と説明できたことと同じように考えてみよう。
自力解決の様子
A つまずいている子
(1㎡の図を用いて考えている)
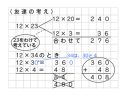
[MATH]\(\frac{4}{7}\)[/MATH]×2だから、[MATH]\(\frac{4}{7}\)[/MATH]㎡を2個かいてみよう。
B 素朴に解いている子
(同数累加で考えている)
[MATH]\(\frac{4}{7}\)[/MATH]×2だから、[MATH]\(\frac{4}{7}\)[/MATH]を2回足してみよう。
C ねらい通り解いている子
(単位分数で考えている)
[MATH]\(\frac{4}{7}\)[/MATH]は[MATH]\(\frac{1}{7}\)[/MATH]でみるといくつになるかで考えてみよう。
学び合いの計画
Aの子のなかには、「[MATH]\(\frac{8}{14}\)[/MATH]㎡」と考える子供がいると予想されます。このような子供がいたら、分数の意味を学び直させるチャンスです。
イラスト/横井智美