小２算数「かけ算(2)」指導アイデア（12/17時）《３倍した長さを比べる方法》

2021.10.30

本時のねらいと評価規準

(本時12/17時九九の構成の後のかけ算の意味の拡張)

ねらい
同じ倍数をかけても、もとの数の大きさが異なれば、かけ算の答えが異なることを考える。

評価規準
もとの大きさの違いに着目し、同じ倍数をかけても、もとの大きさの大小によって、かけ算の答えも大小することについて考えている。(思考・判断・表現)

ミニカーが1台あります。 2ばいの台数に色をぬりましょう。3ばいの台数に色をぬりましょう。

ミニカーの長さは4cmです。ミニトラックの長さは6cmです。それぞれ、3ばいの数をたてにならべると、どちらが長いですか。

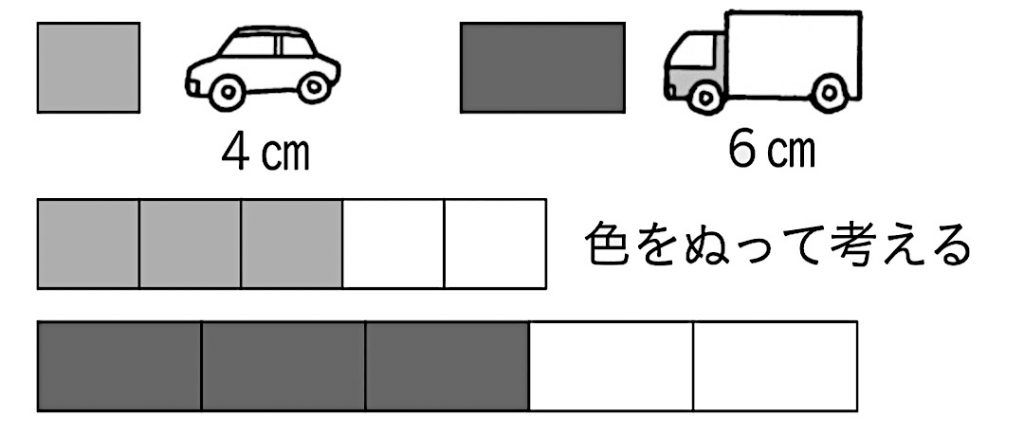
はじめに「2つ分が2倍、3つ分が3倍」ということを算数用語として指導します。ミニカーは、一つ一つの大きさの誤差も少なく、同じ大きさのものが複数ある場面も違和感のない素材です。準備の問題として、色塗りをさせると取り組みやすく、理解を促せます。「倍」の意味をみんなが理解した後で、問題場面を提示します。

ミニカーとミニトラックの数をどちらも3倍にします。どちらが長くなると思いますか。

どちらも同じ3倍だから、長さは同じになると思います。

もとの長さが違うから、同じ長さにはならないと思います。

もとの長さが長いミニトラックのほうが、長いはずです。

かけ算が使えそうです。

ミニカーとミニトラックのどちらが長くなるのかを予想させ、自力解決の時間を取りましょう。

ミニカーとミニトラックを３倍した長さを比べる方法を考えよう。

どちらも、3つ分の長さを調べればよさそう。

A つまずいている子
同じ3倍だから、同じ長さになる。(3倍を操作の回数として捉えている)

B 素朴に解いている子
ミニカー 4×3=12
ミニトラック 6×3=18
12cmのミニカーより、18cmのミニトラックのほうが長い。(3倍した長さを比較している)

C ねらい通りに解いている子
同じ3倍するのなら、もとの数が大きいほうが長くなる。(もとにする1つ分の長さに着目している)

イラスト/松島りつこ・横井智美

『教育技術小一小二』2020年11月号より