スッキリした分かりやすい構成で、子どもたちに伝わりやすい板書の書き方を目指す本シリーズ。今回は、小五の算数の「分数のたし算」「分数のひき算」をテーマにして、 樋口万太郎先生（京都教育大学附属桃山小学校教諭）に、 前時の学習とのつながりを意識させ、理解を深めるようにするための構造的板書について解説していただきます。
目次
算数スキル１：考え方を並列に並べる
★分数のたし算
異分母分数のたし算の計算の仕方について考える時間です。
「 [MATH]\(\frac{1}{2}\)[/MATH]+[MATH]\(\frac{1}{3}\)[/MATH]」の問題を提示し、
分母同士をたします。2 ＋ 3 は？
5
分子同士をたします。1 ＋ 1 は？
2
ということは、 [MATH]\(\frac{1}{2}\)[/MATH]+[MATH]\(\frac{1}{3}\)[/MATH] = [MATH]\(\frac{2}{5}\)[/MATH] だね
え!? 違うよ!?
どうして [MATH]\(\frac{2}{5}\)[/MATH] ではないの？ じゃあ、考えてみよう
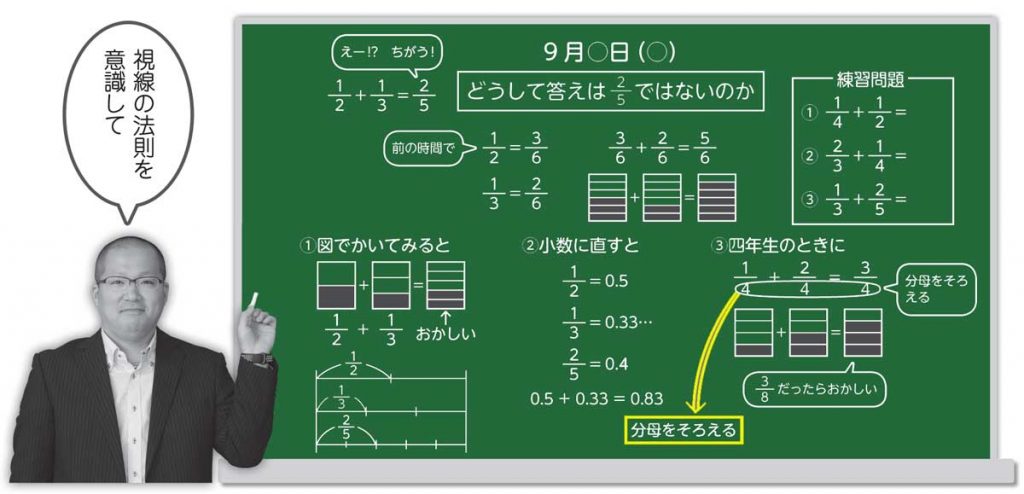
授業冒頭、このように子供たちに問いかけます。どの子もこれらの会話の中で、この答えが違うことに気づきます。そこで、 [MATH]\(\frac{2}{5}\)[/MATH] ではない理由について考える時間を取ります。子供たちからはこれまでの学習により、「図から考える」「分数から小数に直して考える」「四年生で学習した同分母分数の学習を元に考える」などといった考え方が出てくることでしょう。
この時、なかなか考えることが難しい子は、教科書やこれまでのノートを元に考えさせます（前時までに約分や通分について学習しています）。
視線の法則で、Ｚの法則、Ｆの法則というのがあります。
Ｚの法則とは、紙やコンビニの棚などを見る際に、左上 → 右 → 左下 → 右と「Ｚ」の順番に視線を動かすという法則のことです。Ｆの法則とは、左上 → 右 → 最初に見た左上 → 少し下 → 右と「F」の順番に視線を動かす法則です。
全体を見渡すときには「Z」の動きをすることが多く、全体の構成を把握した後は、お目当ての情報を探すために「F」の動きをすることが多いそうです。
そういった視線の法則にも当てはまるように、出てきた考え方を上の板書例の下半分のように並列で書いていきます。多様な意見や考え方が出てくるときには、並列で書くことで、
分類・比較・関連づけしやすい
という効果があります。
考え方を共有した後は、正しい計算の仕方について考えていきます。このときには、「どうして [MATH]\(\frac{2}{5}\)[/MATH] ではないのか」で考えた考え方を使うことができるので、それほど難しくなく正しい計算の仕方について考えることができます。
算数スキル２：既習を「つなげる」
構造的板書を描いていく上で大切にしたいことの1つは、「つなげる・つながる」という意識を教師がもっておくことです。この意識がないと授業も板書もスムーズにはいかないことでしょう。
★分数のひき算
異分母分数のひき算の計算の仕方について考える時間です。このページの実践はスキル１の実践の続きです。
「 [MATH]\(\frac{3}{4}\)[/MATH] － [MATH]\(\frac{2}{3}\)[/MATH] 」の問題を提示し、
分母同士をひきます。4 － 3 は？
1
分子同士をひきます。3 － 2 は？
1
ということは、 [MATH]\(\frac{3}{4}\)[/MATH] － [MATH]\(\frac{2}{3}\)[/MATH] = [MATH]\(\frac{1}{1}\)[/MATH] 、1 ということだね
え!? 違うよ!? 絶対違う！
どうして [MATH]\(\frac{1}{1}\)[/MATH] ではないの？
スキル１と同じ展開であるため、「前回と一緒」といったつぶやきが子供たちから必ず聞こえてきます。このとき、子供たちの中では前回の学習と今日の学習が「つながり」はじめています。そこで、「前回はどんな学習をした？」と問い返すことで、子供たちは前時の学習を振り返ります。授業冒頭で「前時の振り返りをします」と言う場合と今回の場合では、今回のほうが子供たちがより目的意識をもって、前時の振り返りをします。振り返って、子供たちが表現したことを左側に板書しておくことで、前時の学習との「つながり」が見えてきます。算数科は既習や既有体験をもとに考える教科です。考え方などもつながっています。
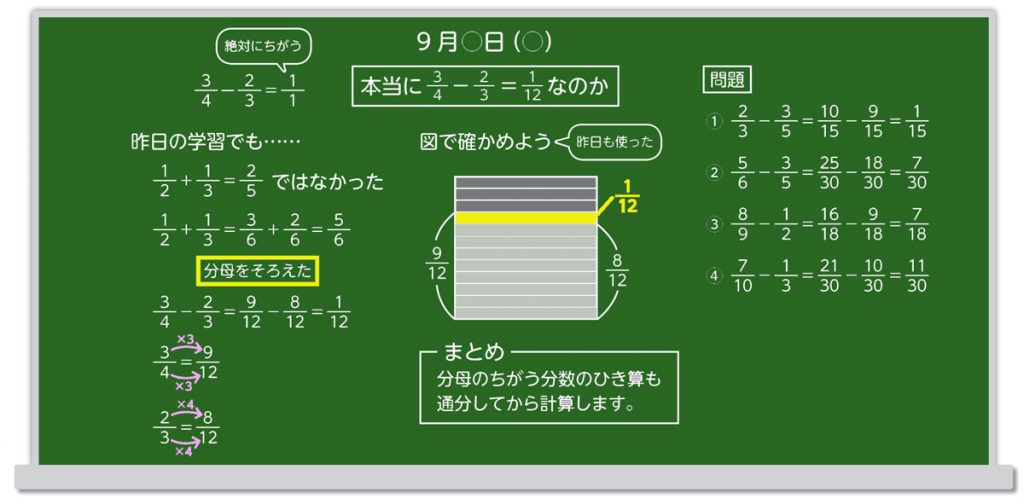
この後、 [MATH]\(\frac{3}{4}\)[/MATH] － [MATH]\(\frac{2}{3}\)[/MATH] の答えを前時の学習である「分母を揃えないといけない」という考えを使い、教師のほうで [MATH]\(\frac{1}{12}\)[/MATH] という答えを示した後に
「本当に [MATH]\(\frac{1}{12}\)[/MATH] で正解なのか」
と問いかけ、考える時間を取ります。このときも前時の学習を元に考えることができます。図をもとに考えることで、理解を深めます。最後は問題を数問解くことで、定着させます。
この時間で、子供たちも「つながり」を改めて実感することができるでしょう。このような授業を行うためには教師が授業をぶつ切りで考えず、つながりを意識しながら、作る必要があります。だから、私は単元ごとに授業を考えていくことをオススメしています。
『小五教育技術』2018年9月号より
★小学館『みんなの教育技術』Webサイトでは小学校の先生に役立つ情報を毎日発信中★ぜひお気に入り登録して最新記事をチェックしてください！
↓↓↓
『みんなの教育技術』トップへ
