小6算数「点対称な図形の性質」指導アイデア
執筆/埼玉県公立小学校教諭・播元和貴
編集委員/国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
(本時6/12)
ねらい
対応する点、辺、角の性質や、対応する点を結ぶ直線と対称の中心との関係の性質を理解する。
評価規準
点対称な図形の性質について、対称の中心や構成要素に着目して考えている。(数学的な考え方)
問題
下の点対称な図形について調べましょう。
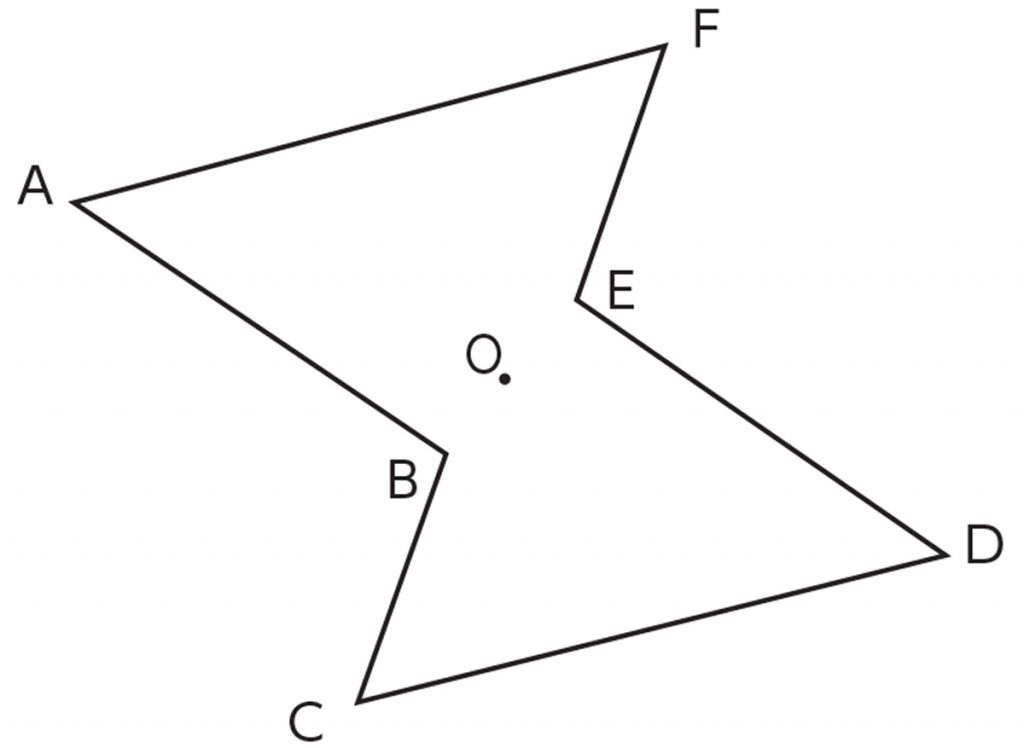
点対称な図形とは、どのような図形でしたか。
対称の中心Oの周りに180°回転させた時に、ぴったり重なる図形です。
そうでしたね。では、左の図形を180°回転させた時に、頂点Aと重なり合う頂点はどれですか。
頂点Dです。
辺EFと重なり合う辺はどれですか。
辺BCです。
そうですね。このように、点対称な図形で、対称の中心Oの周りに180°回転した時に重なり合う点、辺、角を、それぞれ対応する点、辺、角と言います。
線対称な図形の時と似ています。
では今日は、線対称な図形の時と同じように、点対称な図形の特徴を調べていきましょう。
本時の学習のねらい
点対称な図形の特ちょうを調べよう。
自力解決
どのようなことを調べますか。
対応する辺の長さや角の大きさについて調べたいです。
対応する頂点どうしを結んだ直線と、対称の中心との関係はどうかな?
線対称な図形の時は……?
A つまずいている子
・調べる観点が分からない。
・図形を回転させた時の対応が捉えられない。
B 素朴に解いている子
・具体物を操作しながら考えている(辺や角などの構成要素にはふれていない)。
・対応する点を結び、対称の中心Oで交わることを捉えている。
C ねらい通りに解いている子
・具体物を操作するだけでなく、辺や角などを測りながら対応を考えている。
・線対称な図形の時の考え方を基に、対称の中心Oから対応する2点までの長さを測っている。
学び合いの計画
ここでは、子供がコンパスや分度器を使ったり、具体物を操作したりして、点対称な図形の構成や性質を理解することをねらいとしています。
イラスト/やひろきよみ
『小6教育技術』2018年4月号より