小学校理科の評価の観点④【より妥当な考えをつくりだす】とは？ 【進め！理科道〜よい理科指導のために〜】#13

｢進め！理科ロード」では、小学校理科に関する基本的な考え方について、発信していきます。前回から具体的な方法や考え方についてもUPしはじめました。しばらくは、｢評価」について連載していきます。
理科の評価の観点で一番理解しにくいのは、｢思考・判断・表現」の観点です。平成29年の学習指導要領の小学校理科では、「思考・判断・表現」の観点については「問題解決の力」が身についているかどうかで評価をすることになりました。ここでの「問題解決の力」は、｢問題の見いだす」｢根拠ある予想や仮説を発想する」｢解決の方法を発想する」｢より妥当な考えをつくりだす」の4つの力を指しています。つまり、｢思考・判断・表現」の観点の評価は、｢問題解決の力」と呼ばれている「問題を見いだす」｢根拠ある予想や仮説を発想する」｢解決の方法を発想する」｢より妥当な考えをつくりだす」の４つの力ができているかどうかで判断することになります。

執筆／國學院大學人間開発学部教授・寺本貴啓

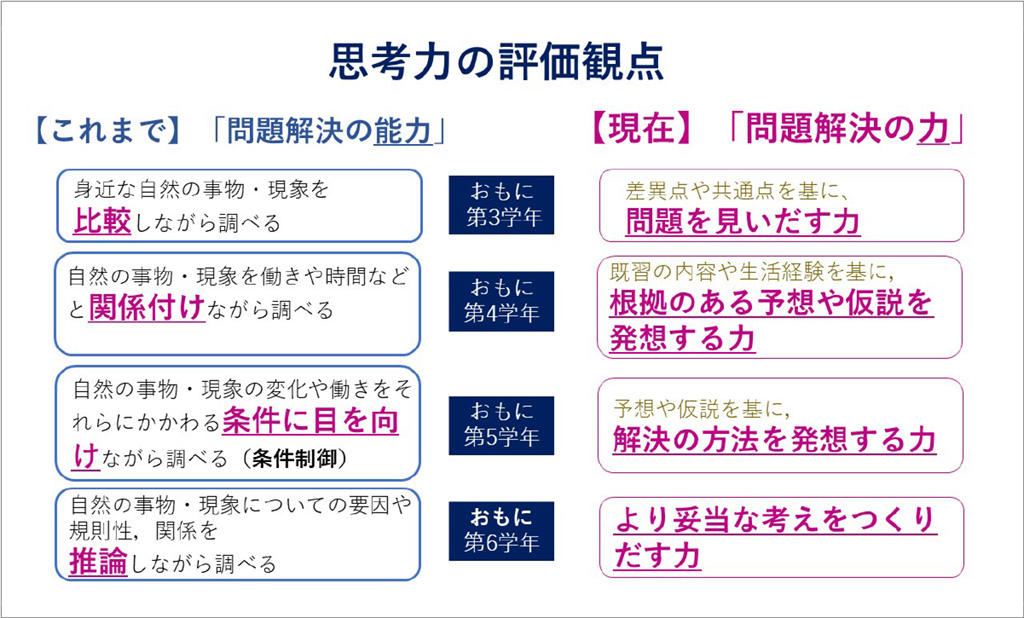
前回までは、思考力の評価の観点になる「問題を見いだす力」｢根拠ある予想や仮説を発想する力」｢解決の方法を発想する力」の評価について確認しました。今回は、いよいよ最後４つめの「より妥当な考えをつくりだす力」の評価について確認していきましょう。｢解決の方法を発想する力」は、主に６年の「思考・判断・表現」の観点として評価することになっています。

【大好評連載 寺本先生の「評価の観点」シリーズ過去記事はこちら】
小学校理科の評価の観点③【解決の方法を発想する】とは？
小学校理科の評価の観点②【根拠のある予想をする】とは？
小学校理科の評価の観点①【問題を見いだす力】とは？
小学校理科で大きく変わった「思考・判断・表現」の評価とは！？

1．科学的にみることは、｢今考えられるより良い判断」をすること

私たちが何かを判断する際には、｢できるだけ良い選択をしたい」ですよね。例えば、買い物をするときに、たくさんあるリンゴの中でどれを選んだらおいしいだろうか？ と考えた際には、時期や品種、色、形など様々な視点から判断するのではないでしょうか。

理科においても、実験をする際に、｢予想が正しいのか確かめたい」｢正しい結果を導きたい」と思いますし、｢みんなが納得する結論を出したい」と思うのではないでしょうか。そのため理科では、育成したい思考力の観点として「より妥当な考えをつくりだす力」があります。

より良い選択ができる、みんなが納得できる説明や判断ができる、といった意味が含まれる「より妥当な考えをつくりだす力」をつけるために、理科では「実験結果から解釈し、何が言えるのか判断して説明する」ことを重視しています。つまり、｢考察を書く際に、実験結果から妥当な判断がなされたかどうか」という力が求められるといえます。

しかしながら、｢より妥当な考えをつくりだす力」が求められるのは「実験結果から考察をする場面」だけかというと、ほかの場面でもありそうです。

小学校理科における「より妥当な考えをつくりだす力」はどのようなおことを指すのか整理してみましょう。

2．｢より妥当な考えをつくりだす力」とは？

｢より妥当な考えをつくり出す力」とは、以下のように大きく２つに分けて考えられます。それぞれについて確認してみましょう。

（1）一般的には、｢結果から考察を書く際に、妥当な判断ができるか」を問うている

まずは、先ほどから述べている、｢結果から考察を書く」場面における「より妥当な考えをつくりだす力」について考えましょう。こちらの方は第６学年の思考力の評価をする際にはこの場面で評価するのが一般的なのではないかと思います。

問題解決は、まず子ども１人１人に自らの問題があって、予想や仮説をもって観察や実験をする流れが一般的ですよね。そして、自分の予想や仮説が正しいのか、結果から判断するわけです。 例えば、第５学年の振り子の実験で考えてみましょう。

振り子の１往復する時間が「振り子の長さ」｢おもりの重さ」｢振れ幅」のどの条件が関係しているのかということを調べる実験があります。このとき、｢ふりこが１往復する時間は何によって変わるのだろうか」という問題ができたとします。そして、次のような結果を得たとします｡（数値は１往復の時間：10往復をはかり、１往復分を出す→３回やって平均を出すなどの方法を行う）

●振り子の長さの条件だけを３種類変えたとき（10ｇ・20度）

●おもりの重さの条件だけを３種類変えたとき（30㎝・20度）

●振れ幅の条件だけを３種類変えたとき（10ｇ・30㎝）

この結果（時間としての数値）から、おもりの重さと振れ幅の条件では、それぞれ重さや振れ幅を３種類変えても１往復の時間はそれほど変わっていない一方で、振り子の長さの条件の時だけほかの条件と比べて大きく１往復の時間が違っている（長くなればなるほど遅くなる）ことがわかります。

この場面を「より妥当な考えをつくりだす力」の観点で考えてみます。今回の実験結果はあくまでも〇〇秒という「時間」を指しますが、まずは、
①この単なる数値から「何が言えるのか」｢共通性があるのか」｢ほかの条件と違いがあるのか」という視点でみて、｢振り子の長さの条件を変えた時だけ時間が変わっているが、ほかの条件では時間が変わっていない」ことを導きます（事実の読み取り・分析）。
次に、
②「振り子の長さの条件を変えた時だけ時間が変わっているが、ほかの条件では時間が変わっていない」と読み取ったことから、｢振り子の長さを変えると1往復の時間が変わる」｢長くなればなるほど往復の時間が遅くなる」｢おもりの重さや振れ幅を変えても1往復の時間を変えることはない」という解釈を導きます（解釈）。
さらに、
③各班の結果も同じような結果なのか、違う振り子でも同じことが言えるのかを検討します（一般化）。

このように、｢結果から考察を書く」場面において妥当な判断をする例として、
①結果を正しく読み取っているか
②数値の読み取りから正しく解釈できているか
③自分たちの数少ない結果だけで判断していないか
といういくつかの観点があることがわかります。このような観点が子ども個々でできているかどうかで「より妥当な考えをつくりだす力」があるか判断します。

（2）「結果から考察を書く」以外にも妥当な判断をする場面はたくさんある

｢結果から考察を書く」場面だけ「より妥当な考えをつくりだす力」があれば、理科全体として「より妥当な考えをつくりだす力」があるというのはちょっと厳しいと思いませんか。

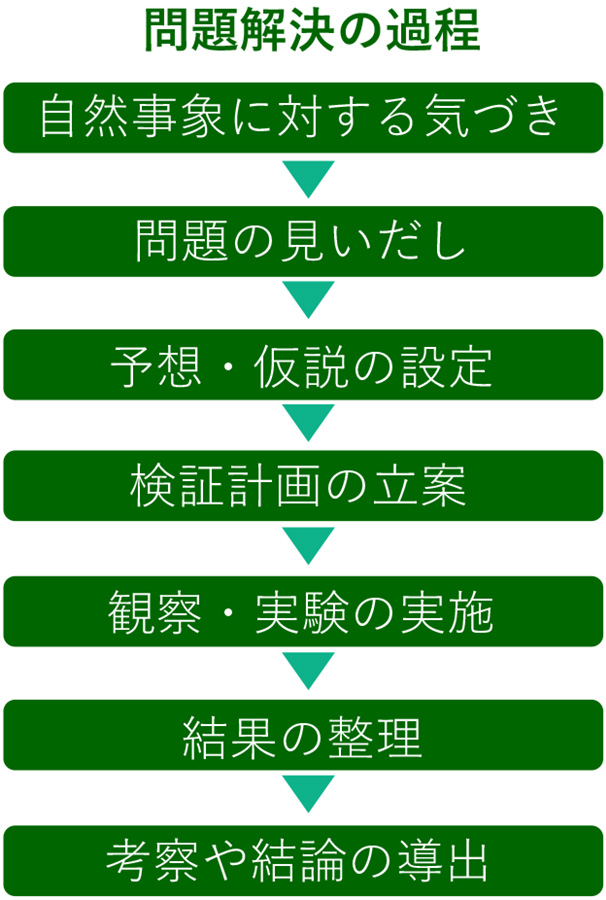
理科の問題解決は、判断の連続です。そのため、｢より妥当な考えをつくりだす力」が求められる場面はたくさんあります。以下の問題解決の過程の各場面からその一例をみてみましょう。

これから理科の時間で調べていく問題を設定する際に、子どもが自分自身で「問題が目的に合っているものか」｢理科の時間で調べられることなのか」｢自分でやりたいことなのか」など、自分が考えた問題や学級の問題を設定する際に「問題を見直すこと」が「より妥当な考えをつくりだす力」が求められる場面に該当すると考えられます。

問題を設定した後に自分自身の予想・仮説を設定する際に、子どもが自分自身で「予想・仮説が問題と正対しているのか」｢予想の根拠が確からしいといえそうか」｢自分が本当に考えていることなのか」など、自分が考えた予想・仮説を設定する際に「見直すこと」が「より妥当な考えをつくりだす力」が求められる場面に該当すると考えられます。

問題が決まり、自分の予想があるとき、検証計画（自分の予想が正しいのか確かめる方法）を設定する際に、子どもが自分自身で「検証計画が問題と正対しているのか」｢検証計画が自分の予想を確かめられる方法なのか」など、自分が考えた解決方法を検討する際に「見直すこと」が「より妥当な考えをつくりだす力」が求められる場面に該当すると考えられます。

検証計画が決まり、実際に観察や実験を行う際に、子どもが自分自身で「問題解決するために正しい方法をしているのか」｢安全なのか」｢調べたいことが調べられているのか」｢正しい結果が得られるように気を付けているのか」など、自分が考えた解決方法を行う際に常に「見直すこと」が「より妥当な考えをつくりだす力」が求められる場面に該当すると考えられます。

このようにみてみると、問題解決の場面では常に自分がやっていることや自分の判断が正しいかどうか見直し、より妥当な考えになるように考え続けているということがわかります。

理科は本来ならば、問題解決過程全般で、より妥当な考えをつくり出している活動ですし、理科が「科学的」と言われる所以でもあるといえるでしょう。

評価としては、問題解決全般までやってしまうとパンクしてしまいます。あくまでも教師側の意識と言いますか、努力事項程度なのかなと思いますが、少なくともまずは結果から考察を書く際により妥当な判断ができるようにしていきたいものです。

3．どうやって「解決の方法を発想する力」を評価するか？

（1）｢結果から考察を書く際に妥当な判断ができるか」の場合

６年の思考・判断・表現の評価としてＡＢＣをつける場合、｢Ｂ基準」としては、上述した
①結果を正しく読み取っていること
②数値の読み取りから正しく解釈できていること
を大切にしたいため、結果（事実）から解釈が書ければよいと思います。結果をもとに解釈できていない（例えば、解釈だけでその根拠となる事実を書いていない）場合や「全く異なった解釈」｢そもそも事実が読み取れていない（結果データが読めていない）」は、｢Ｃ」になると思われます。

｢Ａ」となると、③自分たちの数少ない結果だけで判断していない、など、一般化に向けた視点まで考察や発表で説明できるとよいのではないでしょうか。

６年の思考・判断・表現の評価として最低でも１単元で１か所は評価します（複数単元で学期の評定をする）。

（2）「結果から考察を書く」以外の場面の場合

６年の思考・判断・表現の評価としてＡＢＣをつける場合、１つの単元の中で（1）を全く評価せず（2）だけを評価するというのはあり得ません。もしもほかの場面でも評価をする際には､（1）でできているかを見たうえで、｢Ａ」をつけるかどうかを判断する際の観点としては良いのではないでしょうか。

【「評価の観点」シリーズ過去記事はこちら】
小学校理科の評価の観点③【解決の方法を発想する】とは？
小学校理科の評価の観点②【根拠のある予想をする】とは？
小学校理科の評価の観点①【問題を見いだす力】とは？
小学校理科で大きく変わった「思考・判断・表現」の評価とは！？

「進め！理科道」は、隔週金曜日に更新いたします。

「このようなテーマで書いてほしい！」「こんなことに困っている。どうしたらいいの？」といった皆さんが書いてほしいテーマやお悩みを大募集。先生が楽しめる理科授業を一緒に作っていきましょう!!
※採用された方には、薄謝を進呈いたします。

＜著者プロフィール＞
寺本貴啓●てらもと・たかひろ　國學院大學人間開発学部 教授 博士（教育学）。小学校、中学校教諭を経て、広島大学大学院で学び現職。小学校理科の全国学力・学習状況調査問題作成・分析委員、学習指導要領実施状況調査問題作成委員、教科書の編集委員、NHK理科番組委員などを経験し、小学校理科の教師の指導法と子どもの学習理解、学習評価、ICT端末を活用した指導など、授業者に寄与できるような研究を中心に進めている。

イラスト／難波孝