小2算数「はこの形」指導アイデア(5/5時)《ティッシュばこのような形を組み立てよう》
執筆/富山大学人間発達科学部附属小学校教諭・屋鋪善祐
編集委員/文部科学省教科調査官・笠井健一、前・富山県公立小学校校長・中川愼一
目次
本時のねらいと評価規準
(本時5/5時 箱の面の形や数、辺や頂点の数を学習後)
ねらい
長方形や正方形などの形をした面の特徴や位置関係に着目し、箱の形を作り上げる方法について考える。
評価規準
長方形や正方形などの形をした面の特徴や位置関係に着目し、箱の形の構成について考えている。(思考・判断・表現)
問題
ティッシュばこのような形を組み立てよう!
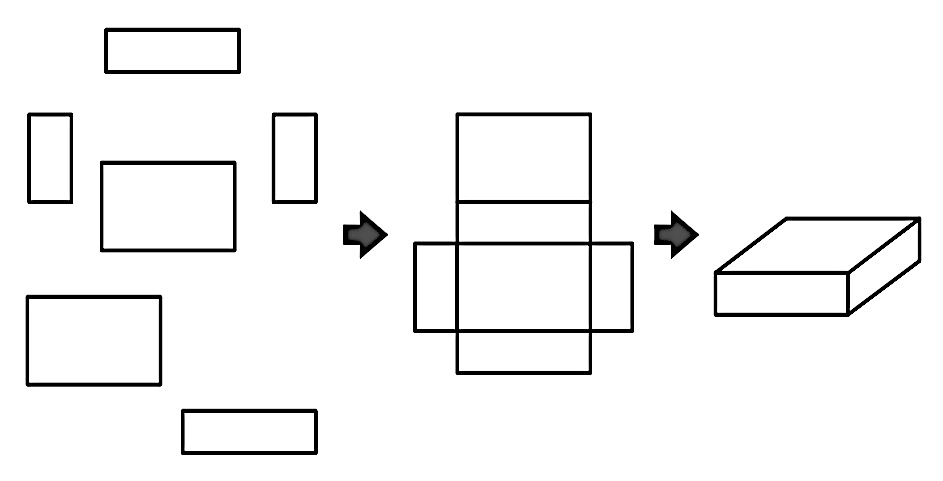
面をつなげて、ティッシュの箱のような形を組み立てましょう。面をどのようにつなげていけばよいですか。
(実物を触りながら……)十字の形になるように並べればできます。
みんなで試してみましょう。
(追体験)……、できました!
まだ別のつなげ方でもできそうだよ!
つなげ方は1つではないのですか。
面の場所を移動すればできそうです。別の方法もありそうです! 作ってみたいな!
最初、子供たちに「ティッシュ箱のような形を組み立てよう」と投げかけ、マグネット付きの色板を6枚(長方形2枚×3セット)を配付します。子供たちは、試行錯誤しながら色板をつないでいくでしょう。
机間を回りながら、多くの子たちが見いだした考え(十字型)をもつ子を指名して、前に出て組み立てる場を設けます。「そう、そう! できる!」と周りの子たちは反応するでしょう。「本当に!? じゃあ、実際に試してみよう」と投げかけ、全員で確認する場を設けます。「やっぱりできた!」とつぶやく子たちのなかに、「まだ別のつなげ方でもできるよ」と話す子が出てきます。そこで、「つなげ方は、1つではないの」と全体に投げかけることで、「まだまだあるよ! もっと見付けたい」という子供たちの意欲を高めていきます。
学習のねらい
どんなことに気を付けて、面をつなげばよいのだろう。
見通し
- 同じ長さの辺をぴったり合わせると、うまくできそうだ。〔方法の見通し〕
- つなげ方に何かコツやきまりがありそうだ。〔結果の見通し〕
自力解決の様子
A つまずいている子
同じ長さの辺をつなげていない。
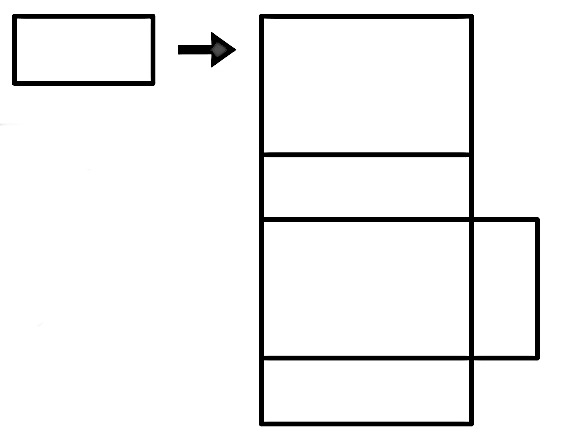
あれ? 箱の形に組み立てられないよ…
B 素朴に解いている子
同じ長さの辺をつなげて、別の面のつなげ方を見いだしている。
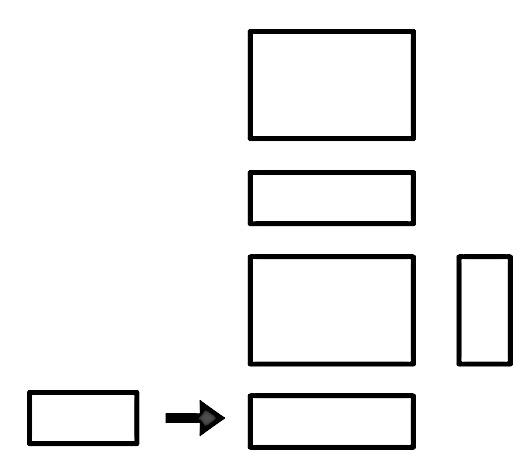
同じ辺の長さの所につなげればいいよ!
C ねらい通りに解いている子
辺の長さや面の位置関係に着目して、さまざまな面のつなげ方を見いだしている。反例についても見いだしている。
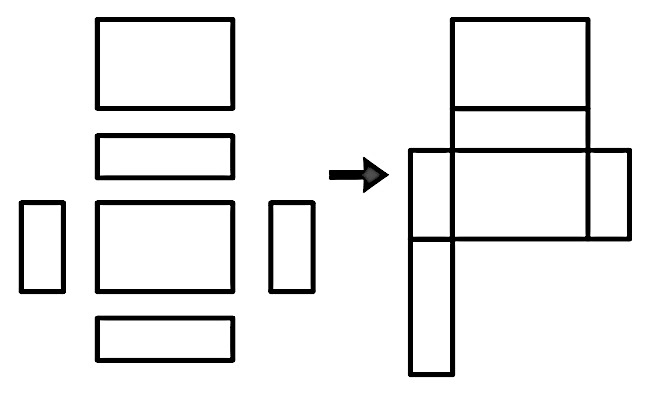
同じ大きさの面は、向かい合うようになっている! もし、同じ面が隣同士だったら、重なってしまうからできない!
どんな面のつなげ方をしたのですか。
イラスト/横井智美
『教育技術 小一小二』2021年3月号より