小5算数「速さ」指導アイデア
執筆/島根県公立小学校教諭・肥後和子
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
ねらい
速さの比べ方を考えることを通して、速さは単位量あたりの大きさの考えを使って、数値化して表せることを理解する。

評価規準
・速さの比べ方を時間と距離の2つの量を基にして、単位量あたりの考えを用いて数値化して考えようとしている。
・問題場面を理解し、目的に応じた速さの比べ方、考え方を説明しようとしている。

ぱっと見ただけで、すぐに速さを比べられる人はいますか。
BさんとCさんは、走った距離が同じ40mなので、かかる時間が短いBさんが速いです。
AさんとCさんはかかった時間が同じなので、走った距離が長い、Aさんの方が速いです。
では、50mを9秒で走るAさんと、40mを8秒で走るBさんでは、どちらが速いでしょうか。
時間も距離も違うから……?
どちらかがそろっていれば、比べられるけど。
本時の学習のねらい
かかった時間と走ったきょりがちがう、AさんとBさんの場合の速さの比べ方を考えよう。
見通し
どうすれば、時間も距離も違う2人の速さを比べられますか。
時間か距離のどちらかをそろえれば、比べられると思います。
どんなそろえ方がありますか。
距離もかかった時間もバラバラだから、どちらかをそろえればいい。
単位量あたりの考えを使って、1秒あたりに進む距離で比べる。
1mあたりにかかる時間でも、比べられると思う。
自力解決の様子
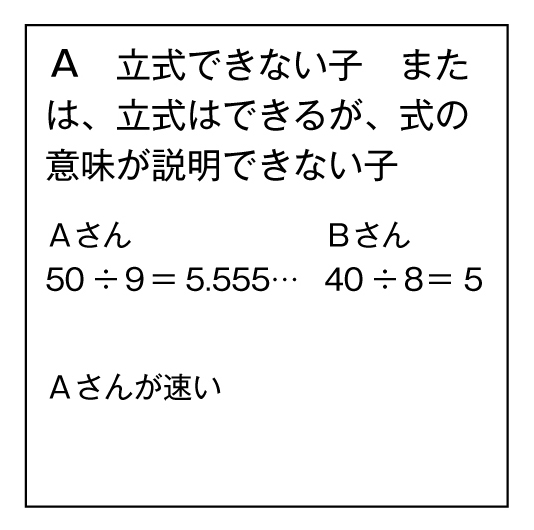
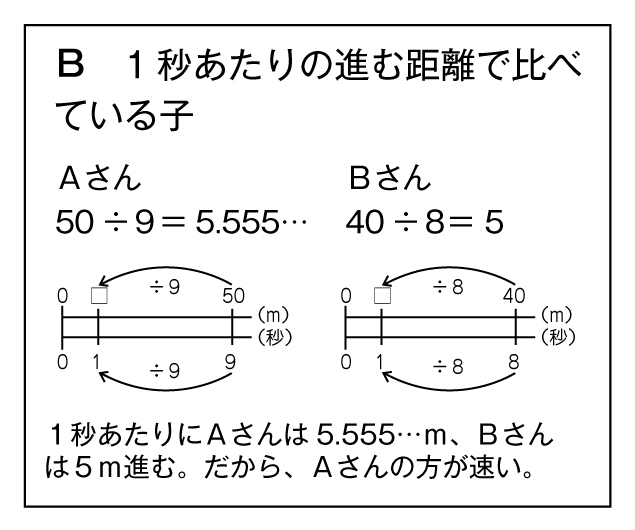
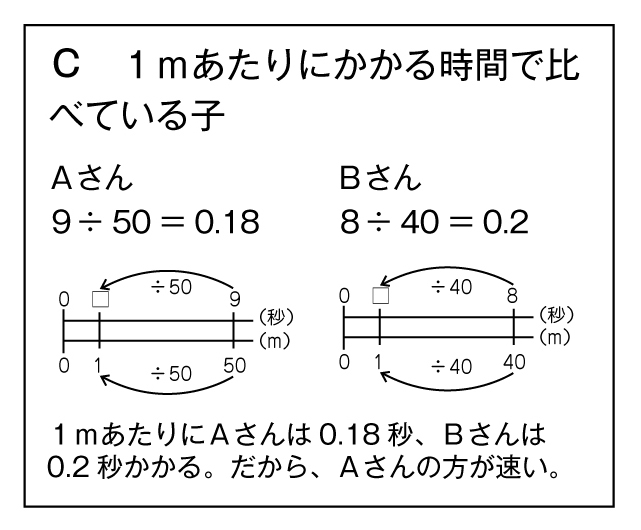
本時のノート例
イラスト/横井智美
『教育技術 小五小六』 2019年12月号より