小5算数「合同な図形」指導アイデア
執筆/お茶の水女子大学附属小学校教諭・久下谷明
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
[本時の位置 4・5/9]
ねらい
合同な三角形を描くのに、すべての構成要素を調べる必要がないことを理解し、合同な三角形を描くことができる。
評価規準
合同な三角形を描くには、3つの辺、3つの角のうち、ある3つの構成要素を用いれば描けることを理解し、実際に描くことができる。
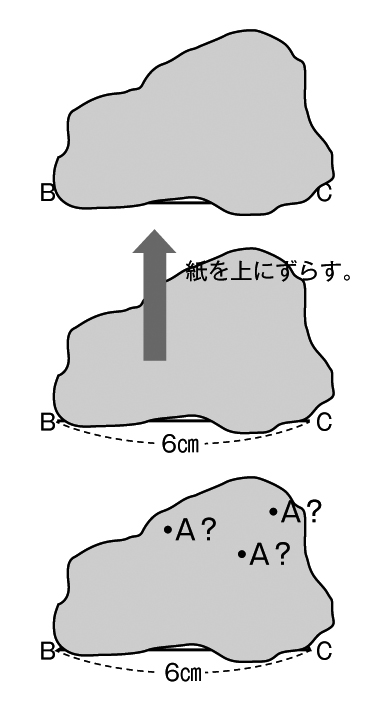
この紙の下には、ある三角形ABCが描かれています。この三角形と合同な三角形を描きたいと思います。隠されている三角形の何がわかれば、合同な三角形が描けそうですか。
辺の長さがわかれば描ける。
角の大きさも……。
(やりとりを通して、3つの辺、3つの角、計6つの構成要素があることを確認した後)では、そのうちの、例えば、辺BCの長さを示しますね。これで三角形ABCと合同な三角形を描けますか。
描けないよ。だって、辺BCの長さがわかっても、頂点Aがどこにあるのかわからないから。
そうですね。逆に、頂点Aの位置がわかれば、3つの頂点の位置が決まるので、合同な三角形が描けますね。まずは辺BCの線を引きます。これで、頂点B、頂点Cが決まりますね。残りの頂点Aの位置を決めるため、辺AB、辺ACの長さ、角A、角B、角Cの大きさのうち、どれを使えばよいかを考えましょう。
本時のねらい
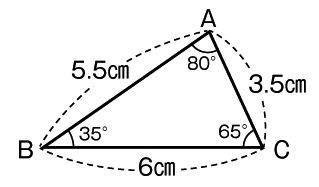
三角形ABCと合同な三角形を描きます。辺BCの他に、何がわかればよいかを考え、合同な三角形の描き方を考えましょう。
見通し
辺BCの他に、何がわかれば、つまり、どの辺の長さや角の大きさを使えば、合同な三角形を描くことができそうですか。
辺BCの長さの他に、辺ABの長さと角Bの大きさでできそう。
例えば、辺BCの長さと辺ABの長さだけだと、描けないのですか。
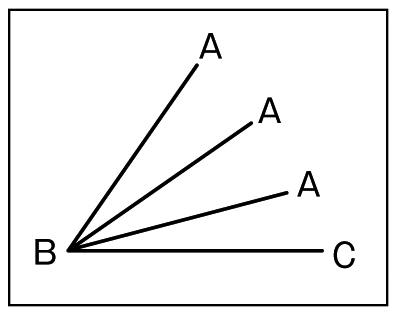
描けないよ。だって、こんなふうに(下図)角Bの大きさがわからないと、頂点Aがいろいろな位置になっちゃうから。
なるほど。
他の方法もあるよ。
では、実際に描きながら、描き方を考えましょう。その時、辺BCの長さの他に、どの辺の長さやどの角の大きさを使ったのか、メモを残しましょう。できたら、別の方法でも考えてみてください。
自力解決の様子
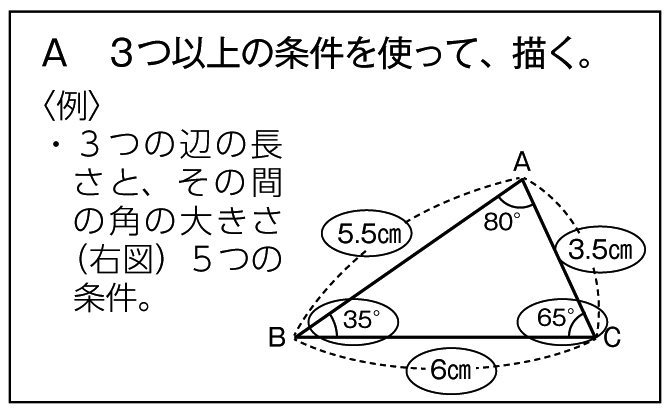
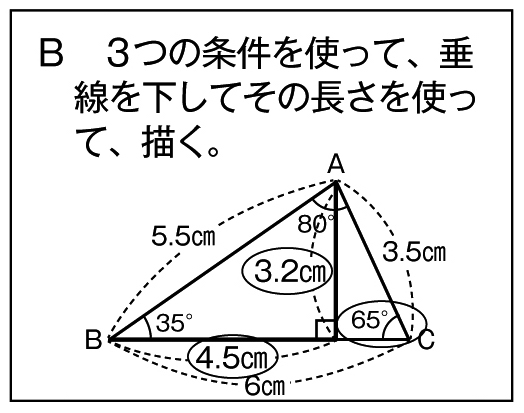
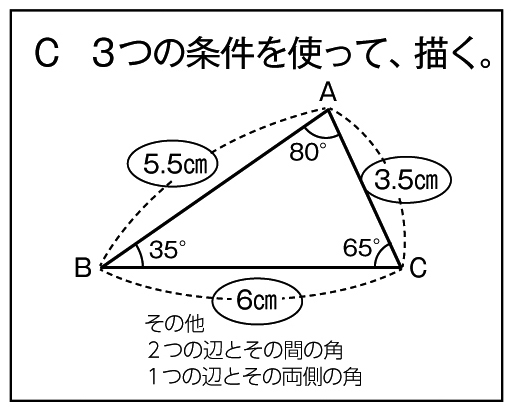
学び合いの学習
見通しをもって自力解決に入ったとしても、具体的にどうしたらよいのかと悩み、手が止まってしまっている子もいます。考えている際中であれば、その姿勢を価値付けるとともに、必要に応じて隣同士で相談し合う、教え合う活動を取り入れるようにしましょう。また、全体発表に入る前には、3人〜4人のグループとなって、友達の考えた方法を聞き合い、共有する時間をとります。
イラスト/横井智美
『教育技術 小五小六』 2019年7/8月号より