小4算数「角の大きさ」指導アイデア
執筆/新潟県公立小学校教諭・清野佳子
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・遠藤昇
目次
本時のねらい
本時1/7時
ほかの量と同じように、角の大きさを比べるときも単位とする大きさを決めて、そのいくつ分で表せばよいと考えている。

評価規準
三角定規の角の大きさを基に、示された角の大きさをいくつ分で表すことを考えることができる。(数学的な考え方)

問題
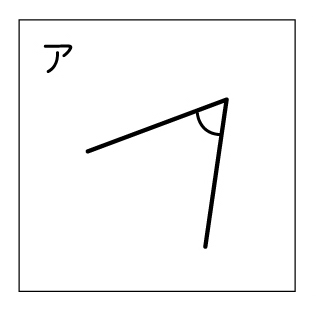
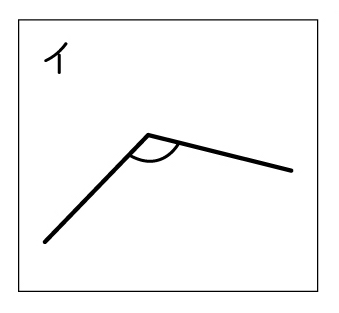
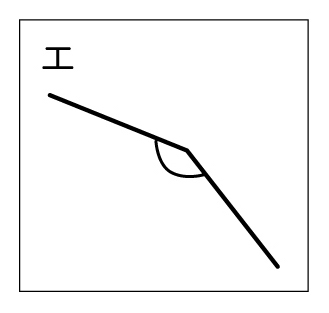
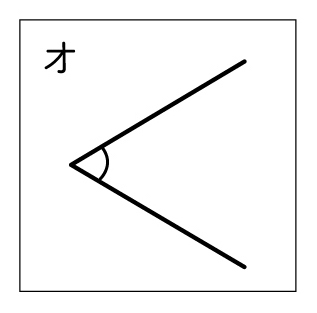
体操をしている5人を上から見ました。足を大きく開いている順に並べましょう。
角の大きさと辺の長さを混同する子供がいます。そこで、辺が開くイメージをもちやすく、複数の辺の長さになる問題場面を提示しましょう。ここでは子供の生活経験に基づき、体育で開脚して体操をしている場面を提示します。
どんな順になりそうですか。
エが一番大きくて、ウが一番小さいと思う。
イはエより小さそうだけど、はっきりしない。
アとオはどちらが大きいか全然分からない。
学習のねらい
どのように調べると大きさが分かるかな。
見通し
頂点の部分。とんがり具合を調べれば分かる。
辺の端。端と端の離れ具合を調べれば分かる。
自力解決の様子
A つまずいている子
辺の端から端までの長さを測って比べてみよう。
・角の大きさと辺の長さを混同し、辺の長さが長いと角の大きさが大きいと考えている。
B 素朴に解いている子
紙に写し取って、重ねて比べてみよう。
・重ねてはみ出たほうが大きい、はみ出ないほうが小さいと考えている。
C ねらい通り解いている子
三角定規の角をあてて、いくつ分になるかで比べてみよう。
・任意の単位を決めて、角の大きさを数で表そうと考えている。
学び合いの計画
イラスト/横井智美
『教育技術 小三小四』2020年6月号より