小5算数「図形の面積」指導アイデア
執筆/東京都公立小学校教諭・依田理恵子
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 7/13
ねらい
既習の面積の求め方を用いて、台形の面積の求め方を考える。
評価規準
既習の図形に帰着して、台形の面積の求め方を考え、既習の公式を活用して面積を求めることができる。
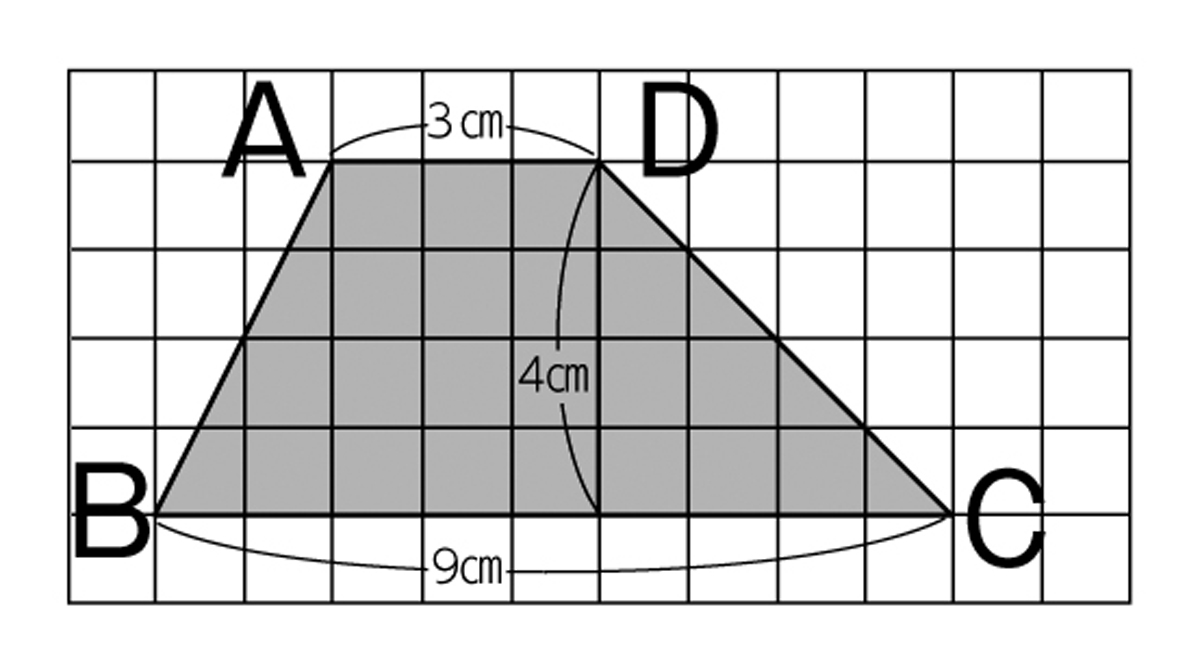
今日はこの図形の面積の求め方を考えましょう。どんな図形ですか。
台形です。
平行な線が一組ある四角形です。
面積の求め方は、まだ学習していないな。
本時の学習のねらい①
これまでに学習した形を使って、台形の面積の求め方を考えよう。
見通し
どうすれば、台形の面積が求められますか。
平行四辺形や三角形の面積を求めたときと同じように、面積の求め方を知っている形に変えればよい。
平行四辺形や三角形に形を変えられるかな?
できる、できる!
面積を求めることができる図形に形を変えて、台形の面積を求めましょう。どのようにすると、形が変えられそうですか。
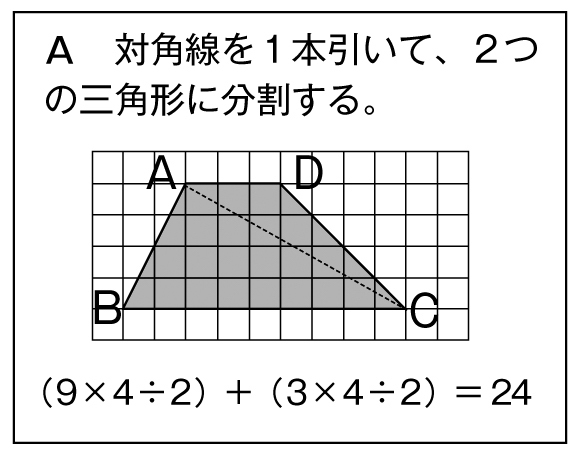
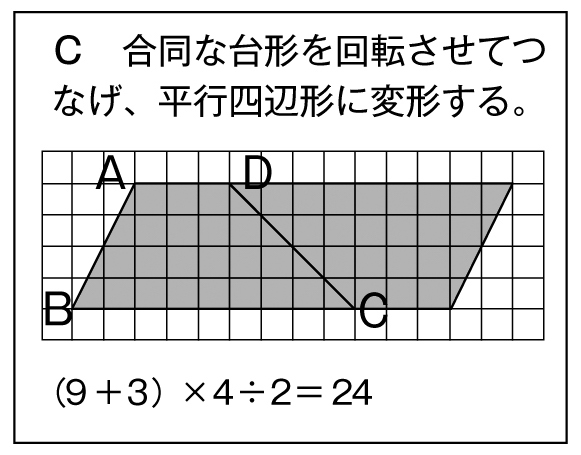
2つに分ければ、三角形が2つできる。
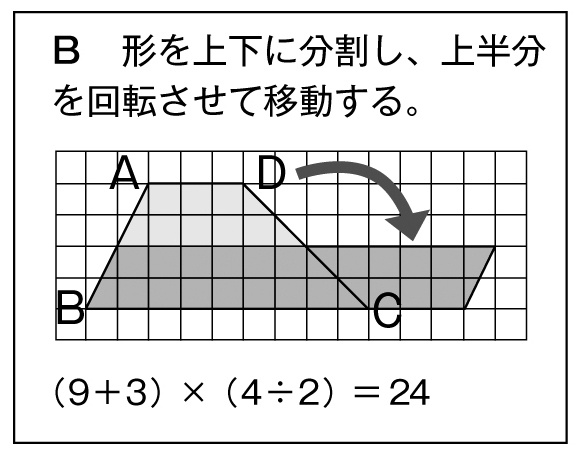
2つ合わせれば、平行四辺形ができそうだ。
平行四辺形に変える方法は、他にもありそうだよ。
本時の学習のねらい②
面積を求めるために必要な長さだけを測って、計算で求めよう。
台形を平行四辺形や三角形に変えることができれば、面積は求められますか。
できる。でも、面積を求めるためには、長さが必要だよ。
すべての長さが必要ですか。
平行四辺形でも三角形でも、(底辺)と(高さ)だけわかればよい。
では、実際に台形をどのように形を変えたのか、面積を求めるために必要な長さはどこなのかを考えながら、この台形の面積を求めましょう。
自力解決の様子
学び合いの学習
イラスト/横井智美
『教育技術 小五小六』 2019年10月号より