子供の考えや思いを引き出して教材にすることが大切 【授業づくり&学級づくり「若いころに学んだこと・得たこと」第24回】

前回、前田正秀先生が富山大学教育学部附属小学校に異動し、｢厳しい仲良し」の仲間たちの中で、算数の本質に関わる「楽しい授業」を追究していったことなどを紹介しました。今回は、そこから考え、整理していった算数の教材づくり、授業づくりのポイントや今、若い先生方に伝えていきたいことなどを紹介していきます。

教材づくりにおける４つの視点

前回、｢なるほど」から逆算しながら、｢あれっ？」｢どうして？」の生まれる教材づくりを大事にするようになったことを紹介しました。そのように、｢算数の本質」に向かう「楽しい授業」をつくるためにいろいろ考えていく過程で、それまで学んだ多様な理論や先輩方の教えが、授業の具体とつながっていったわけです。その頃に試行錯誤して考え、整理した教材づくりの視点は、先の「あれっ？」｢どうして？」を含めて４点あります。

まず「あれっ？」｢どうして？」が生まれる教材が一番大事だと思いますし、その考え方は前回お話しした通りですが、２つ目は、切実感が生まれる教材ということです。身近な素材やゲーム性のあるものを教材に取り入れると効果的だということで、例えば、４年生の「折れ線グラフ」の学習をするときにも実際に体育の1000m走で100mごとのラップタイムを使ってグラフにしていけば、それを見て「一定のスピードで走るようにするには…」などと、グラフに表わすことの効果や意味、必要性もより実感できるはずです。もちろんゲーム性のあるものであれば、子供たちは率先して楽しみながら行い、負けないようにしようとすることで、思考を働かせることでしょう。

３つ目は、適度な負荷がある教材であるということで、子供たちにとってあまりむずかしすぎて、教室内の誰も解決方法を思い付かないような教材だと子供は意欲をなくしてしまいます。逆に、教室内の誰もが簡単に解決方法を思い付くような内容だと多くの子は燃えませんし、意欲をもてません。だから、適度な負荷がある教材であることが必要なのです。

４つ目は、多様な考えが生まれる教材であることです。説明するまでもないと思いますが、多様な考えが生まれるからこそ、その後、考え方の違いを対話していくことで、より理解も深まるものだと思います。

準備不十分の授業のほうが「楽しい授業」?

このように教材を工夫して、子供が主体的に思考し、理解を深めようと考えてきたわけですが、30代後半くらいから、｢子供の考え自体を教材にできればいいな」と思うようになっていきました。そのきっかけになったのが、４年生を担任していたときの授業参観日の授業です。隣のクラスの先生と交換授業をして、隣の先生がご自身のクラスと私のクラスで専門の国語の授業をされる代わりに、私は両方のクラスで専門の算数の授業をすることにしました。隣のクラスで「面積」の授業をしようと思っていた私は、教材も工夫し、多様な手立てを考え、発問も練りに練って準備万端整えたのですが、それが前日の夜中だったのです。そのため、自分のクラスでやろうと思っていた「計算のきまり」の授業は、考えている最中に寝込んでしまいました。ところが、蓋を開けてみると準備が間に合わなかった授業のほうが、楽しい授業になったのです。

後から、なぜそうなったのかを考えてみたのですが、準備不十分の授業のほうは途中の手立てがない状態でしたから、私は子供たちから出てくる意見だけが頼りでした。もし多様な考え、本質に関わる考えが出てこなかったら、授業が終わってしまうわけで、そのため、私は子供たちの意見に徹底して耳を傾けます。そこから「算数の本質」に関わりそうで、なおかつ気になる考え方を見付けて取り上げていったことが、結果的には「楽しい授業」であり、なおかつ多くの子供が思考し、｢算数の本質」に触れていくような授業になっていきました。

ちなみに、この授業の問題は「丸の数を数えましょう｣（図１参照）というものだったのですが、子供たちがどんな解法を考えているのか、机間を回って見とる私は目を皿のようにして見ていきました。すると、ある子供が「１×２＋３×２＋５×２＋７」という式を書いていたのです。１×２を２とせず、わざわざ１×２と書いたことに、その子の思いが込められていると思い、その子を最初に指名して発表させました。

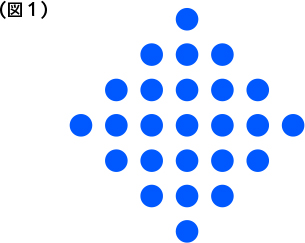
その子の式に対して、｢２と書かないで、どうして１×２と書くんですか？」という問いが、一人の子供から出され、それが教室全体の問いになったのです。その問いに対し、ある子は「数えたり、たしたりしたんじゃなくて、かけ算で求めたってことを表わしたかったのでは？」と言い、別の子は「丸の並び方が左右対称で、右と左が同じ数のペアになっているってことを表わしたかったんじゃないか」と話し、また別の子は「例えば、２＋６＋10＋７だと、どうやって数えたのか分からない。１、３、５、７と数がきれいに並んでいることを表わしたかったのでは？」と推測する子が出てきて、さらに「１×２、３×２…って書いたほうが、どこをどうして２になったのか、何が２個あるのかが分かりやすい」と評価する意見も出てきました。

そうやって数学的に考えながら、とても楽しい授業になったのです。この授業を経験してから、小手先の手立てよりも、子供の考えはもちろん、考えに至った背景や思いを引き出して教材にすることが大切だと考えるようになったのです。

子供の考えを教材化するためには「聴く姿勢」と「教材観」が大事