小2算数「たし算とひき算 図を使って考えよう」指導アイデア(3/5時)《問題文の構造をテープ図で捉える》
執筆/東京都目黒区立中目黒小学校主任教諭・渡辺五大
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 加法逆の問題解決を通して、加法と減法の相互関係についての理解を深める。
▼
第2時 減法逆の加法の問題解決を通して、加法と減法の相互関係についての理解を深める。
▼
第3時(本時)加法逆の減法の問題解決を通して、加法と減法の相互関係についての理解を深める。
▼
第4時 減法逆の減法の問題づくりを通して、場面をテープ図や式に表現し、問題を解決する力を伸ばす。
▼
第5時 学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り価値付ける。
本時のねらい
加法逆の減法の問題解決を通して、加法と減法の相互関係についての理解を深める。
評価規準
場面を表したテープ図を基に、加法逆の減法の問題を解決している。
本時の展開

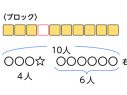
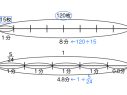
公園に何人かいます。あとから8人来たので、みんなで23人になりました。はじめにいたのは何人ですか。
この問題を解くには、何算を使えばいいでしょうか。
「みんなで」と書いてあるので、たし算だと思います。
でも、足したら「みんなで23人」を超えちゃうよ。
この問題が聞いていることは何ですか。
「はじめにいた人数」です。
「8人来た」んだから、やっぱりたし算かなぁ。
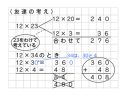
この問題を解くには、どんな式を立てればいいでしょうか。

どんな式になるのか考えよう。
見通し
分かっている数は何ですか。
あとから来た8人です。
みんなで23人です。
分からない数もありますね。
はじめにいた人の数です。
分からない数は、□にしたらいいんじゃないかな。
正しい式を立てるために、どうしたらいいでしょうか。
図に表すと分かりやすくなると思います。
なるほど。分かる数と分からない数を図に表せば、式が立てられそうですね。ではまず、この問題をテープ図にかいてみましょう。
自力解決の様子
A つまずいている子
3つの数量の関係をテープ図に表せない。
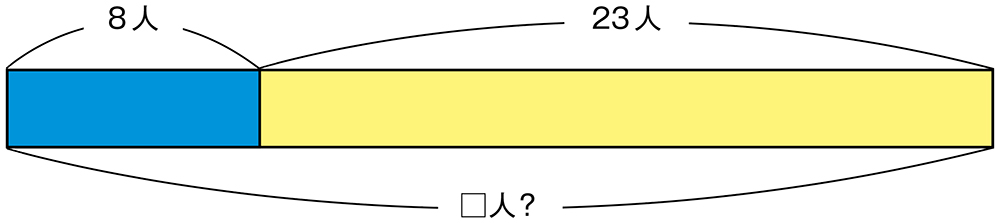
B 素朴に解いている子
3つの数量関係をテープ図に表せる。
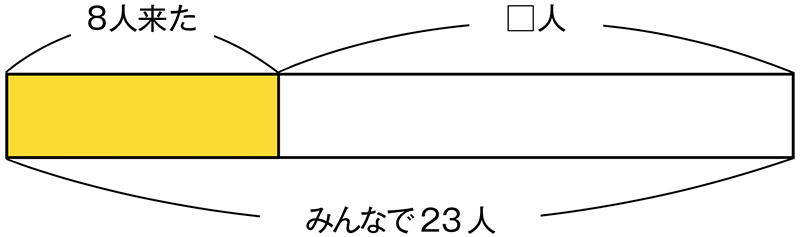
C ねらい通り解いている子
問題文に沿って、時系列に3つの数量関係をテープ図に表せている。
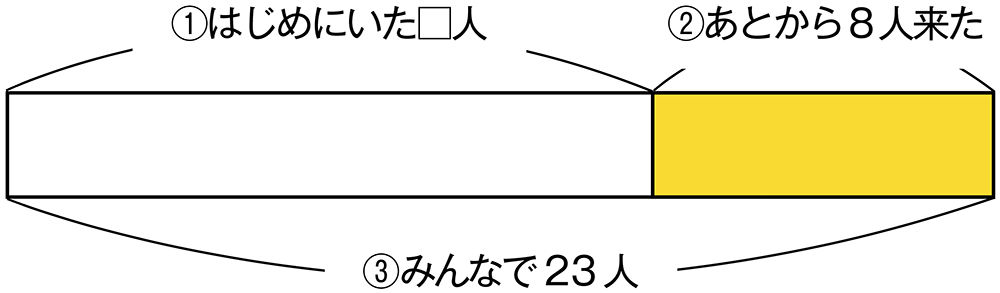
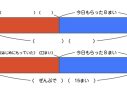
自力解決後、AとCの2つの図を提示し、めあてを焦点化する。
あれ、みんなに図をかいてもらったら、2つの図ができてしまいました。
焦点化しためあて
どっちの図が問題の文に合っているのか考えよう。
※ペアや小集団で話し合う。
では、途中まで図にかいてみましょう。まず、「はじめに何人かいました。8人来ました」まで図にかいてみましょう。
あっ! どちらが正しいか分かった!
では、自分のテープ図を直したり、式が正しいかどうかもう一度考えたりしてみましょう。
学び合いの計画
問題文に出てくる3つの数量を見いだし、問題文の構造を捉えることが本時の最も重要な取り組みになります。
イラスト/横井智美