小学算数「構造的板書」の工夫とコツ（図形の合同／倍数と約数）

スッキリした分かりやすい構成で、子どもたちに伝わりやすい板書の書き方を目指す本シリーズ。今回は、小五の算数の「図形の合同」「倍数と約数」がテーマです。
樋口万太郎先生（京都教育大学附属桃山小学校教諭）に、 情報を整理するためのグループ化と、そのために便利なシンキングツールを紹介していただきます。

算数スキル１：グループで分類する

私が小学生の頃、ある・なしクイズが流行していました。では突然ですが、ある・なしクイズを１問出題したいと思います。

「食う」にはあるけど、「寝る」にはない。
「棒」にはあるけど、「剣」にはない。
「福」にはあるけど、「富」にはない。
「６」にはあるけど、「７」にはない。

さあ、答えはわかりましたか。今はこのクイズが文字で見えるため、考えやすかったかもしれません。しかし、何も書かれずに問題を口頭だけで言われたらどうでしょうか。きっと混乱するのではないでしょうか。情報を頭のなかで整理するのは難しいことなのです。

しかし、ある・なしというグループごとに分類して書くと、とてもわかりやすく、考えやすく、気づきやすくなります。この「グループで分類すること」は算数では多く使われています。

※答えは、記事の末尾にあります。

単元「図形の合同」

単元終末あたりの学習です。この単元を通して「合同」「対応する角や辺」について学習してきています。

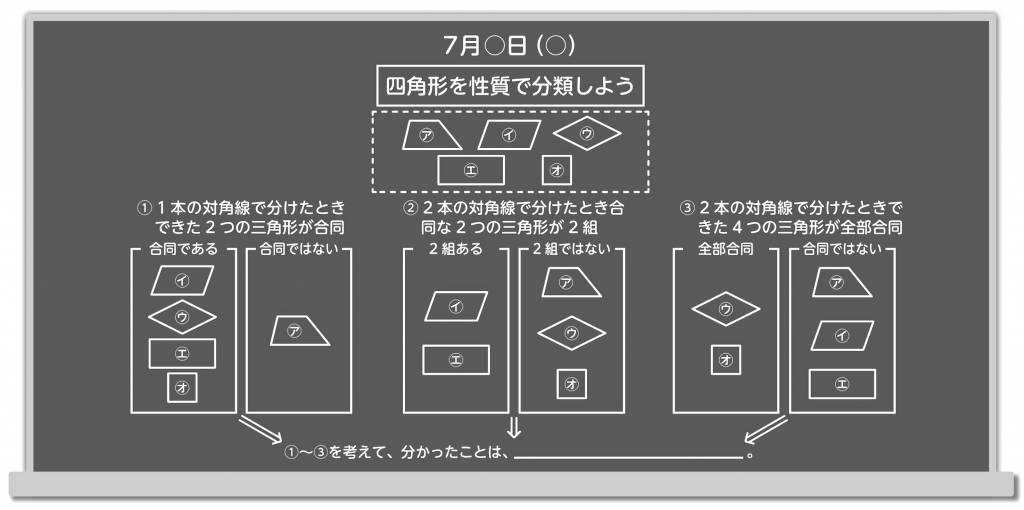
この時間では、台形、平行四辺形、ひし形、長方形、正方形といったこれまでに学習した図形を性質によって分類していく学習をします。「性質で四角形を分類しよう」と提示した後、問題を３つ順番に出して、解決していきます。

１問目　１本の対角線で分けたときできた２つの三角形が合同であるか、合同ではないか。
２問目　２本の対角線で分けたとき合同な２つの三角形が２組ある、２組ではない。
３問目　２本の対角線で分けたときできた４つの三角形が全部合同である、合同ではない。

分類していくとき、５つの図形にはそれぞれにア～オまでの記号がついています。その記号だけで分類した様子を表すのではなく、図形を移動させ分類することで、より分かりやすくなります。図形の中に実際に対角線を引きながら考えたり、理由を発表させたりしても有効です。考えることが難しい子には縮小版の図形を配付し、書き込ませながら考えさせます。

３問目まで考えたあとには、この３問のグループ分けを比較させながら、分かったことを表現させます。その時に「①～③を考えて、分かったことは・・・」と型を与えて、表現させることでどの子も書きやすくなります。

算数スキル２：シンキングツール「ベン図」