小４算数「小数のかけ算とわり算」指導アイデア《小数が何倍かを表すのに用いられることを倍の計算を基に考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.03.16

単元の展開

第１時　数の構成やかけ算の性質に着目し、小数×１桁の数（0.2×７など）の計算の仕方を考える。
▼
第２時　数の構成やかけ算の性質を基にして、小数×１桁の数（2.3×７など）の立式とその計算の意味について考える。
▼
第３時　前時で学習した小数×１桁の数の計算の意味や整数×整数の筆算の仕方を基にして、小数×１桁の数の筆算（2.3×７など）の仕方について考える。
▼
第４時　小数×２桁の数の筆算（2.7×12など）の仕方を理解し、その計算ができるようになる。
▼
第５時　小数の範囲を広げて、[MATH]\(\frac{1}{100}\)[/MATH]の計算（2.38×４など）や積に空位のある計算（4.05×36など）の筆算ができるようになる。
▼
第６時　数の構成に着目し、小数÷１桁の数の計算（0.6÷３など）の仕方を考える。
▼
第７時　小数÷１桁の数（7.2÷３など）の立式と、その計算の意味について考える。
▼
第８時　小数÷１桁の数の計算の意味や整数÷整数の筆算の仕方を基にして、小数÷１桁の数の筆算（7.2÷３など、一の位に商あり、あまりなし）の仕方について考える。
▼
第９時　小数÷１桁の数の範囲を「一の位に商が立たない場合（4.9÷７、4.92÷６など）」に広げて、筆算の仕方を理解し、その計算ができるようになる。
▼
第10時　小数÷２桁の数の筆算（64.8÷36、7.74÷43など）の仕方を理解し、その計算ができるようになる。
▼
第11時　あまりがある場合の小数÷整数の筆算（13.6÷３など）の筆算について考える。
▼
第12時　小数÷整数（15.6÷８など）で割り進みをするときの筆算の仕方を理解し、その計算ができるようになる。
▼
第13時　整数÷整数で割り進み、割り切れない場合の商の概数処理について理解する。
▼
第14時（本時）小数が何倍かを表すのに用いられることを、倍の計算を基に考える。
▼
第15時　学習内容の定着を確認し、理解を確実にする。

本時のねらい

小数が何倍かを表すのに用いられることを倍の計算を基に考え、説明することができる。

評価規準

２つの数量の関係に着目して、小数倍についての図を用いて考え、説明することができる。

本時の展開

ボッチャは、ボールを投げたり転がしたりして、的玉に近付けるスポーツです。ゆたかさんたちは、ボッチャの体験をさせてもらいました。

表は、的玉までのきょりをまとめたものです。それぞれの記録について、ゆたかさんの記録との関係を調べましょう。

①えみさんの記録は、ゆたかさんの記録の何倍ですか。また、りこさんの記録は、ゆたかさんの何倍ですか。

ゆたかさんが８㎝で、えみさんが16㎝だから……。

式は16÷８かな。

ということは、りこさんの記録は24㎝だから、24÷８だね。

数直線図で表すと、こうなりますね。

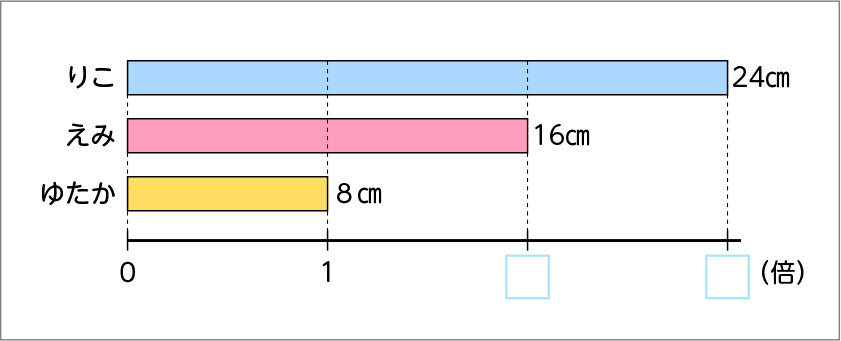
えみさんの記録は、16÷８＝２で２倍です。

りこさんの記録は、24÷８＝３で３倍です。

２倍、３倍とは、どういう意味だったかな。

８㎝の２倍、３倍ということだけど……。

｢２倍」は、ゆたかさんの記録２倍という意味で、｢３倍」は、ゆたかさんの記録の３倍という意味です。

他の人はどうですか。

数直線図を見て分かりました。ゆたかさんの記録の８㎝を「１」として見たときに、えみさんは「２にあたる大きさ｣、りこさんは「３にあたる大きさ」という意味です。

では、次の問題はどうでしょう。

②しょうまさんの記録は、ゆたかさんの記録の何倍ですか。また、ゆづきさんの記録は、ゆたかさんの記録の何倍ですか。

同じようにゆたかさんを「１」として見ると、20÷８だから……。

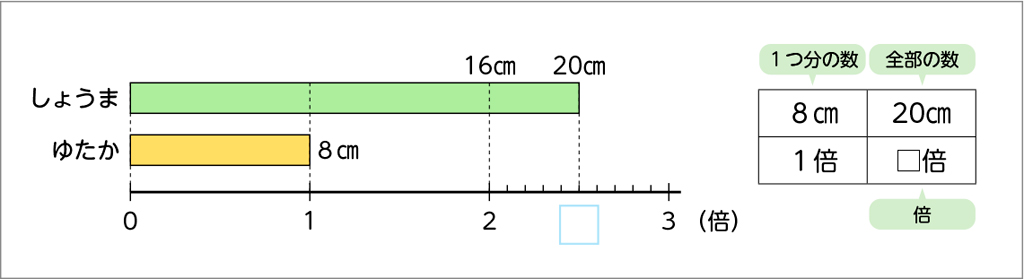
20÷８＝2.5で2.5倍です。

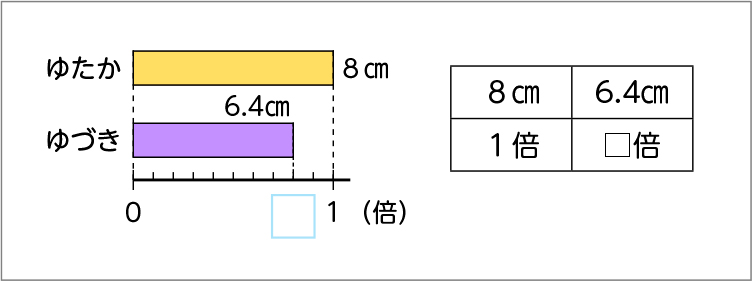
でも、ゆづきさんの記録のほうが短いけど……。

式は6.4÷８でいいのかな。

答えが小数になりそう。

小数のときも、□倍と表してよいのかな。

見通し

2.5倍を説明できますか。どのようにして説明したらいいでしょうか。

数直線図を使えばできます。

表にすると関係が分かります。

１倍よりも小さい倍はあるのかな。

｢全部の数÷１つ分」と考えるとよく分からないな。

では、自分の考えた方法を学習用情報端末に提出してください。（学習アプリを使って無名で自分の考えを出させる）

自力解決の様子

Ａ　つまずいている子
１倍よりも小さい倍の意味が分からず、6.4÷８の逆の計算をしてしまう。

Ｂ　素朴に解いている子
数直線図を使って立式はできたけれども、何を「１」として見るかの説明が難しい。　

Ｃ　ねらい通り解いている子
１より小さい小数で倍を表すことを理解して、図や表に表すことができる。

学び合いの計画

これまでに第４学年「倍の見方」で、整数倍の意味を扱っています。｢５倍というのは２ｍを１と見たとき、10ｍが５にあたる」と指導してきています。１と見る見方は整数で扱っています。今回の小数倍においては、｢基にする量を１と見て、比べられる量が何個分にあたる」かだけでは半端が出てしまうため、基にする大きさを10等分して、0.1にあたる大きさを考えることによって比べられる量にあたる数を探す活動をします。操作としては数直線上で行っており、筆算上では、割り進む計算として行っています。これが小数倍の意味であり、小数倍の意味指導の重点です。図の上での操作と計算上の手続きが同じことをしているところを重点的に扱う必要があります。

そのために、自分の考えを出させる際には、子供が書き込める数直線図や表を、学習用情報端末の子供の考えを一覧で共有できるアプリ（ロイロノートなど）に入れて発表させます。また、大多数の子供の考えを安易に採用するような多数決で決めるのではなく、それぞれの現時点までに分かっている考え方をていねいに説明させましょう。たとえ、自分の考えでなかったとしても、どうしてそう考えたのかを説明させ、正解を言ったとしてもすぐに認めず、他の子に意見を聞き、分かったことを確認して板書していきます。

もし「分からない」という子がいたなら、｢もっと具体的に言える子はいないかな」と聞き、発表させていきます。ペアで分かったことを説明させる交流も取り入れながら、友達の考えを写すだけの授業にならないよう、すべての子供が小数倍の考えを説明できることをゴールにしましょう。自分だけ分かればOKではなく、みんなで分かったことを共有できるように展開し、子供たちが協働で学び合う授業にしていきます。