既習をしっかり生かし、多面的に考えていく授業 【全国優秀教師にインタビュー！ 中学校編　中１〜中３を見通す！ 「高校につながる英・数・国」の授業づくり #24】

前回は、新潟市の授業マイスターである新潟市立新潟柳都中学校の長部賢教諭（数学）に、授業づくりの考え方やその授業を通してどんな子供を育てたいのか聞いてきました。今回は、そのような授業づくりを象徴する授業として、２学年の実践事例について聞いていくことにします。

単元「図形の調べ方」の多角形の外角の和についての授業

長部教諭は今回、２学年の単元「図形の調べ方」の７/17時で、多角形の外角の和についての授業を紹介してくれました。

｢この授業は、どのような多角形でも外角の和が360°になるということを、平行線の錯角や同位角を使って説明ができることに加え、それを一般化していく過程で､（内角の和の学習のように）ｎ角形のｎを使って表していく過程で、最終的にはｎが消えて360°になることも説明できることが重要です。

この授業では、先のような学習のポイントから、まず前時に学習した多角形（ｎ角形）の内角の和についてふり返り、180°×（ｎー２）を確認します。そこから､『では、外角の和はどうなるかな』と投げかけていきます（資料参照）。

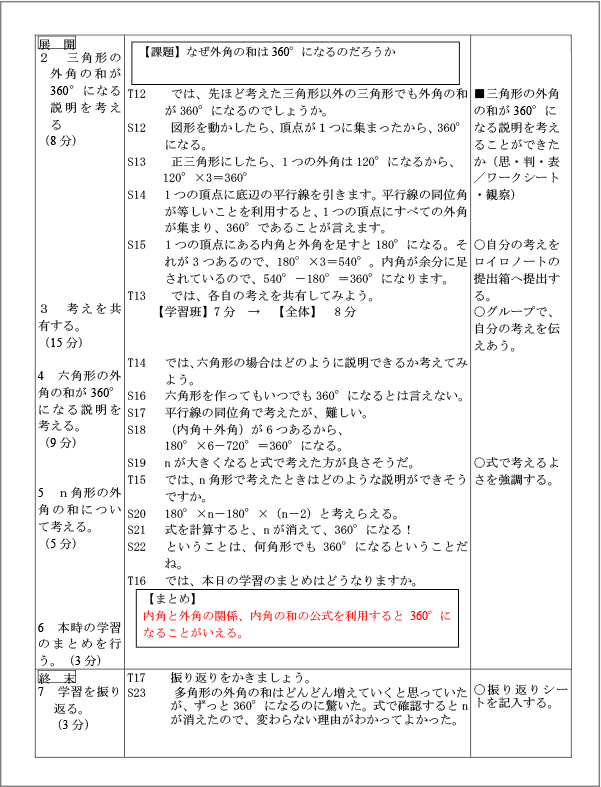
【資料】指導案

ここで、最初に六角形と三角形で予想させるわけですが、前時の学習をふり返って、ｎ角形の内角の和は、180°×（ｎー２）を押さえていますから､『角の数が２倍になるから、外角の和も２倍になる』とシンプルに予想する子供もいれば､『内角が大きくなるので、外角は小さくなるかも』と逆に予想する子供もいて、さらに『（角の数と大小の関係で）ちょうど同じになるかも』と予想する子供もいると考えられます。

そこで、どうすれば『調べられるかな？』と投げかけると、当然、分度器で測ればよいと言うので、実際に測ってみると360°だということが分かります。ここで、既習からの予想や見た目からの予想とのズレが生じるわけで、そこから『では、他の多角形でも外角の和は360°になるのだろうか？』と投げかけると、多数の子供たちが､『四角形や五角形でも360°になりそう』だと言うので､『もしそうだとしたら、今日の課題は何になりそうかな？』と問いかけて､『なぜ、外角の和は360°になるのだろうか』と課題を設定し、まず個人で説明を考えていきました」

ただ、この指導案を作ったときの公開授業では、同じになるのではないかと予想した子供が多かったと話す長部教諭。それについては、授業で提示した六角形と三角形の図が、両方とも正六角形や正三角形に近い形をしていたため、（それぞれの内角の角度を知っていた子供たちにとって）比較的予想しやすかったのではないかという指摘があったと話します。

｢式を使って説明したほうがシンプルで分かりやすい」ということがねらい