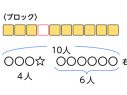
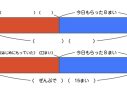
小4算数「わり算1けた」指導アイデア《2位数÷1位数=2位数の暗算の考え方》

執筆/横浜市立篠原小学校教諭・三上顕
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 あまりのない、何十や何百のわり算や、各位とも割り切れる、あまりのない2位数÷1位数の計算の仕方の説明
▼
第2・3時 あまりのない2位数÷1位数の計算の仕方の説明
▼
第4時 各位とも割り切れずあまりのある2位数÷1位数の筆算の仕方の説明
▼
第5時 十の位が割り切れるあまりのある2位数÷1位数の筆算の仕方の説明
▼
第6時 各位とも割り切れない3位数÷1位数=3位数の筆算の仕方の説明
▼
第7時 商に空位を含み、割り切れる3位数÷1位数=3位数の筆算の仕方の説明
▼
第8時 首位に商が立たない3位数÷1位数の筆算の仕方の説明
▼
第9時(本時)2位数÷1位数=2位数の暗算と、商が何十、何百何十になる3位数÷1位数の暗算
▼
第10時 他国のわり算の筆算の仕方を知り、自国のわり算の筆算の仕方と比べる。
▼
第11時 問題に取り組み、学習内容の定着を確認し、理解を確実にする。
本時のねらい
被除数をどのように見て、暗算の仕方を考えたのかを説明し、数の見方を豊かにし、それを利用した能率的な処理の仕方について考える。
評価規準
被除数をどのように見て、暗算の仕方を考えたのか、説明することができる。
本時の展開

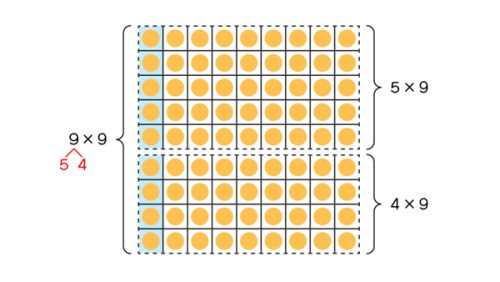
76÷2を暗算しよう。
80÷2は計算できますか。
簡単です。40です。
筆算がいらなくて、暗算でできるんですね。どうしてそんなに早く答えが出せたのですか。
だって、8÷2は4だから。この学習の1時間目にやりました。
なるほど、そうでしたね。さて、どのようなアイデアを使って、80÷2を8÷2と見たのですか。
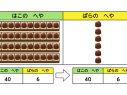
10のまとまりで見ました。
10のまとまりで見ると、8÷2と見られるんですね。この考えを使ったら、ほかにどんな「〇÷2」ができそうですか。
60÷2ならできます。
800÷2もできます。
まとまりで見たら、割られる数が何十、何百の計算は暗算でできそうですね。では、何十、何百ではない数なら暗算でできそうですか。例えば76÷2のような。
難しそうだけど、ちょっと考えてみたいです。
大体どのくらいになりそうですか。
40よりは少なくなると思います。
え、なんで分かるの。
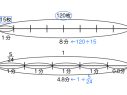
だって、76をだいたい80と見たら、さっきと同じで80÷2が使えて40になります。76は80より少ないから、答えは40よりは少なくなると分かります。
そうかあ。たしかに!
40より小さいとすれば、いくつよりは大きいですか。
30よりは大きいです。
60÷2は30だもんね。
30と40の間だ。なんとなく分かってきた。
だいたい何十と見れば、答えの見通しが立つんですね。10のまとまりなど、まとまりで見るのは便利ですね。では、今まで学習したことなどをどんどん使いながら、76÷2の暗算の仕方について考えてみましょう。

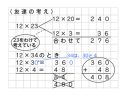
76÷2の暗算の仕方を考え、どのように数を見たのか説明しよう。
見通し
前の学習で、筆算を使わないで答えを出したとき、割られる数を分けて考えたな。(方法の見通し)
九九をうまく使えばできるかな。(方法の見通し)
答えは30と40の間だ。38になりそうだな。(結果の見通し)
自力解決の様子
A つまずいている子
筆算を使えないことで、どのように答えを求めたらよいか分からず困っている。
B 素朴に解いている子
筆算を頭のなかで描いて計算している。
C ねらい通り解いている子
被除数を切りのよい数と九九が適用できる数に分けて試し、どんなところが便利なのか考えている。
学び合いの計画
正しい答えを求められるかだけではなく、暗算をする際に被除数をどのように見たかについて話し合い、よさを共有することで数を豊かにみる視点を養っていきましょう。
イラスト/横井智美