子供たちが知らぬ間に証明の考え方などを身に付けられるような単元構成 【全国優秀教師にインタビュー！ 中学校編　中１〜中３を見通す！ 「高校につながる英・数・国」の授業づくり #5】

前回は、福井県の数学の「授業名人」である福井市明倫中学校の片谷祐樹教諭の、自身の授業づくりの考え方を象徴する授業を紹介していきましたが、その過程で、単元づくりの重要性を何度も強調する片谷教諭。そこで今回は、前回紹介をした「多角形の角」を含む、２年生「図形の調べ方」の単元について紹介していきます。

単元構成において、まず学習内容に対する子供の姿を考えた

片谷教諭は、この「図形の調べ方」の単元構成を考えるときに、まずこの学習内容に対する多くの子供たちの姿を考えたと話します。

｢図形の学習は、多くの子供たちにとって学ぶ意味が腑に落ちず、学ぶ動機が生じにくい学習内容です。図形は身近にいくらもあるのですが、子供たちの心の中では図形の世界と結び付いていません。そのため､『何でこの図形について調べないといけないの？』『何でこれを証明しないといけないの？』と思ってしまうのです。だからこそ、子供たちの中から､『これって、どうなっているんだろう？』『これはなぜ？』という思いが起こって、授業が進んでいくような展開にしたいと思いました」

そこで､『点つなぎ』という子供たちの遊びをうまく使い、点から線、線から面へとディメンションを増やし、イメージを広げるところから学習を進めていったと話します。

｢単元の最初の内容は『角と平行』なのですが、この学習も（先で学ぶ）図形につながるように始めたいと考え､『図形の大本って何？』という問いを投げてスタートしたのです。すると子供たちから『点』ということが出てきます。ただし、１個の点だけではそこから世界は広がりませんから､『点が２つになったら何ができる？』と問うと､『２つの点を結べば、直線ができる』となります。そのときに、改めて180度という世界を考えさせました。

そこで『何で、直線って180度なの？』と問いかけると、子供たちは考えるのですが、算数で習ってきたことが当たり前である子供たちは､『先生、そんなの当たり前だよ』と言うわけです。そこで､『算数では直線は180度だって教えてくれたけれど、小学生にはその理由までは考えられないから、やっていなかっただけなんだよ』と言って考えさせるのです。

私は普段から『無理矢理でもいいから自分なりに理由を付けてみよう。それが正しくても間違っていてもいいから、自分なりに考えたことを皆で持ち寄って考えていったときに考えが収束していくんだよ』と言っているので、子供たちは考えていきます。そして､『１周が360度だから』ということに気付く子どもが現れるのです。そこで、もう１回切り返して､『じゃあ、なぜ１周は360度なの？』と言うと、子供たちは考えながら同時に限界も見えてくるわけです。

そこで、地球は太陽の周りを365日で回っていることから生まれたと言われていますが、自然数自体も同様で、必要だったから人間は多様なものを考えていったんだということに話を進めていきます。子供たちがそういうことに少しでも気付いてくれると､『小学校では分からなかった、180度ということも説明できるのか』とか､『でも、これ以上は説明がむずかしいんだ』ということが分かってきます。そうして180度が改めて分かったところからスタートしていくと、内角や外角の話が出てきたときに、子供たちは180度を根拠に考えるようになっていくのです。

前回、少しお話をしたように､『考える楽しさを味わえるようにしたい』わけですが、何もないところで『考えなさい』と言っても苦しいだけなので、そのような準備をしてから始めていくわけです（資料参照）」

【資料】｢図形の調べ方」単元の指導計画（全15時間）

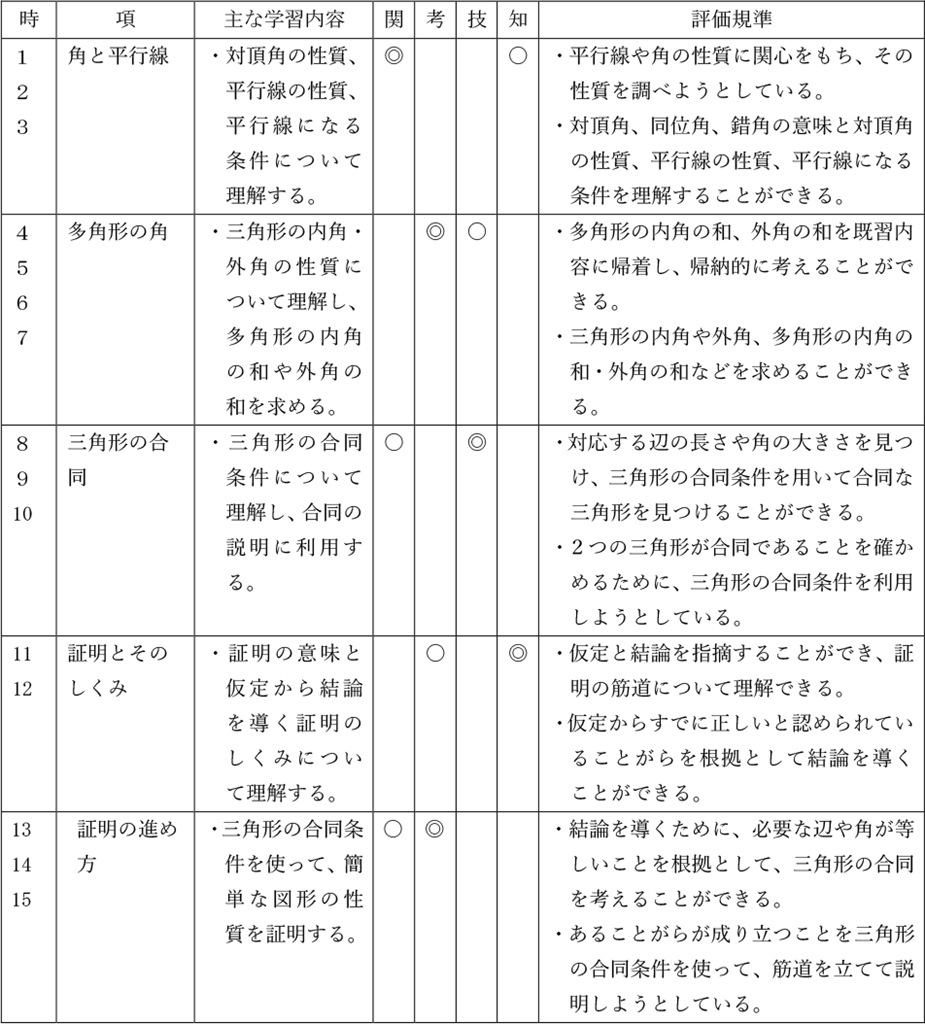
子供たちは自分たちで授業を進めているという気持ちに

そこからさらに、前回紹介した授業を含む「多角形の角」でも、遊び心も交えながら、学習を進めていった片谷教諭。

｢実際に『点つなぎ』の手法で、２点を結んだ線から、３点を結んだ三角形、４点を結んだ四角形、ちょうちょ形、ブーメラン形と点を増やしながら、５点まで点を増やして自由に図形を作らせることから始めました。このように５点まで増やしていくと、教科書に示されているすべての形（三角形、四角形、ブーメラン形、ちょうちょ形、五角形など）を作ることができるのです。その自分たちが作った図形について、どんな特徴があるかを調べていこうという学習の流れにしました。

その中で三角形が出てきたら､『三角形の内角の和は180度。じゃあ、なぜ180度になるの？』ということで、自分たちが身に付けてきた直線は180度ということを使って説明をしてきています。じゃあ､『四角形は？』と考えるときには、三角形の内角の和は180度を使えるようになっています。さらに五角形、六角形となってそれが一般化されていくわけです。また、ちょうちょ形について学習するところでは、対頂角、外角、内角なども全部出てきます。

そうすると、子供たちが作った図形で学ぶべき内容がすべて学べるようになるので、子供たちは自分たちで授業を進めているという気持ちになります。なぜなら前回も説明した通り、自分たちで作った図形で学習が進んでいくし、自分たちが見付けたことが次の学習の根拠になっているわけですから。そういう学習を繰り返していくと､『自分たちが発見したことって、すごい』『自分たちって、できるんだ』と思ってくれるのです」

教師の意図した展開によって、子供が主体的に追究、発見し、それが自信や楽しさを味わうことにもつながるというわけです。

星形の学習を「証明」の入り口として扱う