小6算数「対称な図形」指導アイデア
執筆／東京都公立小学校教諭・大村英視
編集委員／文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 4／12
ねらい
線対称な図形のかき方を考え、説明することができる。
評価規準
既習事項をもとに線対称な図形のかき方を考え、説明している。
問題場面
直線アイが対称の軸になるように線対称な図形をかきましょう。
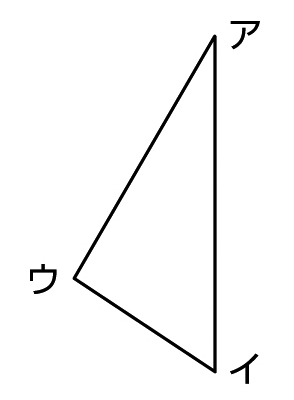
線対称な図形を半分に折りました。広げるとどんな形になるでしょう。
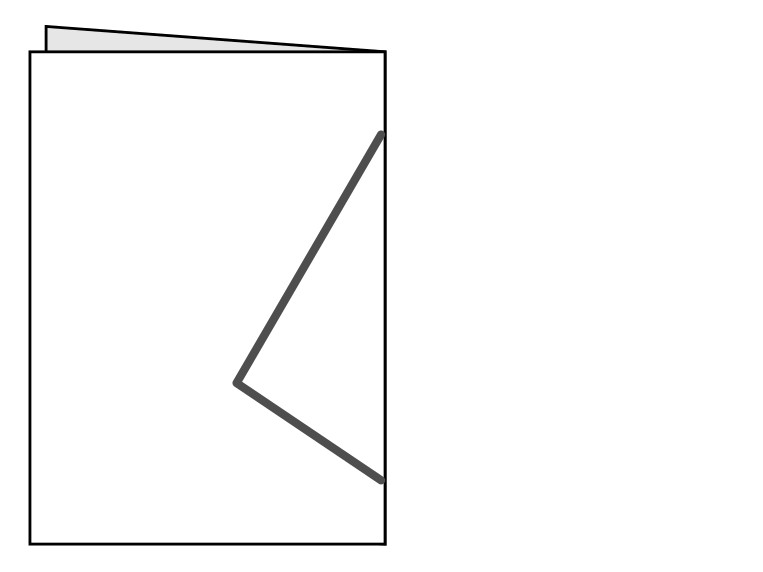
四角形になると思います。
ひし形かな。
ひし形にはならないよ。
広げてみましょう。
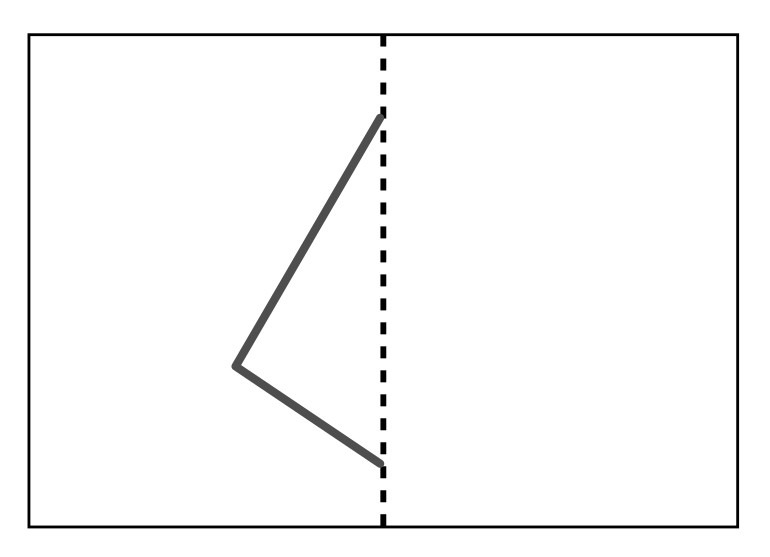
あれ? 図形が半分消えてしまっているよ。
見通し
直線アイが対称の軸になる線対称な図形を完成させましょう。
対応する角の大きさと辺の長さが同じになるようにかけばいいから…。
頂点ウに対応する点の位置を決めるには…。
対称の軸で分けた2つの図形は合同になっているから…。
対応する2つの点を結ぶ直線は対称の軸と垂直に交わるから…。
本時の学習のねらい
これまでに学習した図形の性質を使って、線対称な図形を完成させよう。
自力解決の様子
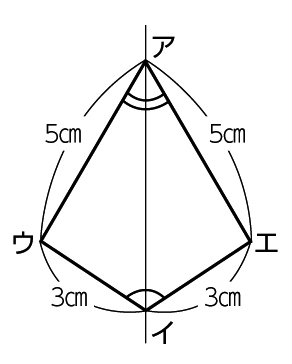
Aの考え方
角アと角イの角度、辺アウと辺アエの長さを測り、三角形アイウと合同な三角形アイエをかく。
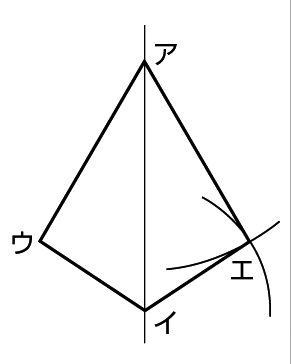
Bの考え方
コンパスで辺アウ、辺ウイの長さを測りとり、ウに対応する頂点エの位置を決める。
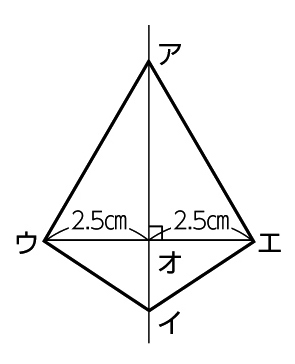
Cの考え方
頂点ウから対称の軸に垂直な直線を引き、ウオと等しい長さを測って頂点エの位置を決める。
学び合いの計画
イラスト／オモチャ、横井智美
『教育技術 小五小六』 2020年4/5月号より
