小6算数「円の面積」指導アイデア《円の面積を既習の図形に見立てて求めよう》
執筆/神奈川県公立小学校教諭・成水亜季
編集委員/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥
目次
本時のねらいと評価規準
〔本時の位置 1/9 図形の観察と求積の見通し〕
ねらい
図形の観察を通して、円の構成要素を基に、既習の図形の求積方法と関連付けて円の面積の見積もりについて考える。
評価規準
円の面積について、既習の面積の測定の仕方を基にして考え、その求積の方法を説明している。 (数学的な考え方)
問題
今日は、円の面積を求めましょう。
難しそうだな。
どうして、そう思いましたか。
今までの図形と違って、直線がない。
1cm²のいくつ分で求めていたけど、円の面積は正確には求めることができないかも。
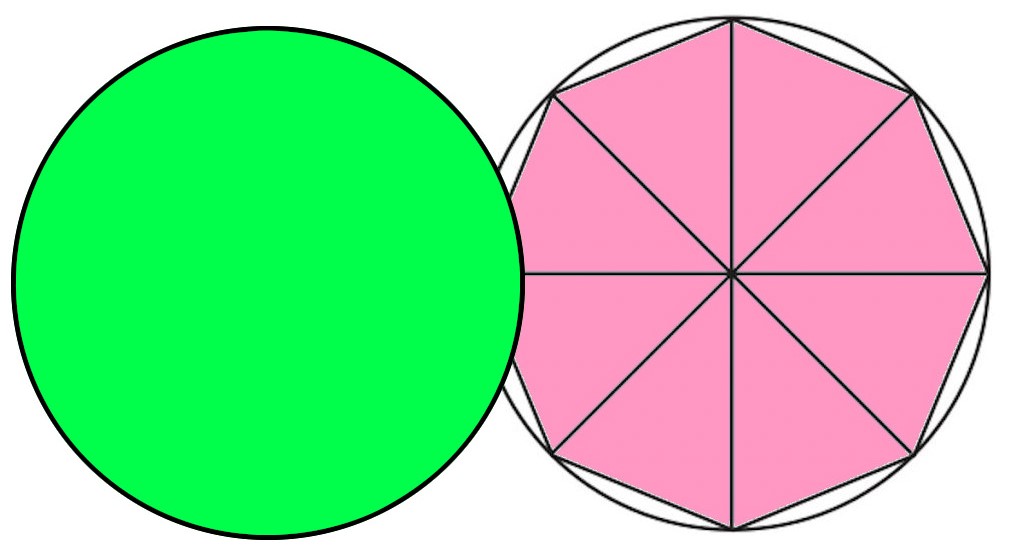
でも、これまで習った図形に見立てて考えれば、およその面積はわかります。
円を観察して、円がどのような図形なのか、どのような図形に見立てられそうか、考えてみましょう。
本時の学習のねらい
円がどのような形か観察し、どうすれば円の面積を求めることができるか考えよう。
見通し
円を半分にして、さらに半分にしても同じ形になります。だから、1/4の円の大きさを求めて、それを4倍したら円の面積がわかります。
1/4にした円の中に三角形が見えます。円の半径はどこも等しいから、直角二等辺三角形と言えます。この三角形の面積を基に、考えることができそうです。
自力解決



学び合いの計画
これまで求積してきた図形と異なり、円は曲線で囲まれています。子供たちには、円の面積を求める前に、円がどのような図形なのかをじっくり観察させ、どのように考えれば面積を求めることができるかを、円の構成要素を根拠に見通しがもてるようにします。
イラスト/横井智美
『教育技術 小五小六』2019年5月号より

