GeoGebraを使った「円」の授業【「高校につながる英・数・国」の授業づくり #58】

今回からは、2025年夏の日本算数・数学教育学会の石川県大会で、石川県の中学校教諭として、ただ一人実践研究発表を行った、金沢市立紫錦台中学校の三浦彩教諭に授業実践の実例やその背景となる教育観、子供観などについて伺っていきます。 初回となる今回は、三浦教諭の授業づくりの考え方を象徴する、3年生の「円」の単元の中の1時間を紹介していきます。

三浦彩 教諭
目次
「円周角の定理」の逆が成り立つかどうかという課題
この授業は、全10時間の単元の中の一次(5時間)の中の5時間目で、円周角の定理について学習した後の授業です。
ここまでの単元の学習を進めるに当たっては、金沢の地図のどこかに人気ゲームキャラが隠れているという場面設定を行い、事前に決めた条件に沿ってゲームキャラの隠れている場所(点P)を探そうというような形で各時間の授業を展開。その中で、円や弦や弧、中心角などの関係を考えていくような単元構成をしていくと三浦教諭は話します(資料4参照)。
ちなみに、地図は権利の関係上、授業で活用した実物をお見せすることはできませんが、三浦教諭が抽象化してくださった地図(資料1参照)からも想像できる通り、実際の金沢市内の地図を利用。実際にある施設やランドマークを使いながら、地図の下に示された条件に沿って、ゲームキャラの隠れている点Pを探すことをクイズ的に楽しみ、問題解決しながら、数学の学びを進めていくわけです。
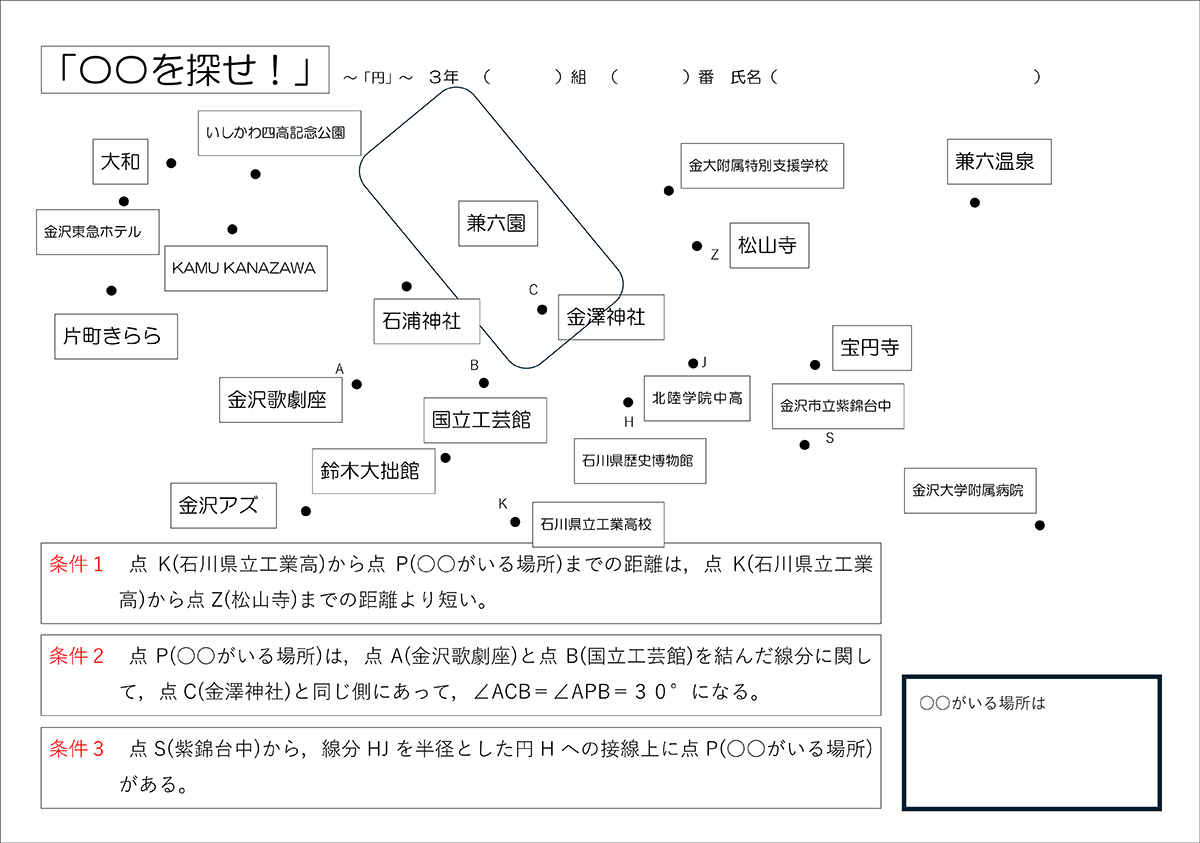
資料1 地図と条件
「今回紹介する授業の学習内容は、端的に言えば『円周角の定理』の逆が成り立つかどうかという課題の学習です。実際のこの授業では、探すべきゲームキャラが隠れている位置Pは、地図上の2点A、Bとの関係が∠APB=30°となるような位置だと条件を設定(点AもBも金沢市内の既存の建物のある場所にすることでリアリティをもたせてある)。子供たちはゲームキャラが隠れている点Pがどこにありそうか、考えていきます(資料2参照)。
資料2 指導案

この学習では、GeoGebraを使い、子供たちが地図上に任意の点Pを設定すると、勝手に∠APBの角度が示されるようにしてあります。すると子供たちは自分で操作活動を行いながら、地図上にあり∠APB=30°となる場所をたどり、その軌跡を残していくわけです。
数学が苦手な子供は、最初の地図と問いだけでは見当も付かないわけですが、GeoGebraを使えば、だいたいの見当が付けられます。それによって、∠APB=30°となる『点Pは、どうやら円周になりそうだぞ』と、円周角の定理の逆が成り立ちそうなことに気付きます。
ちなみに、これまでは中心から距離が等しい点の集まりが円になるということでしたが、ここで初めて同じ角になる点の集まりが円になる、というところに注目できるのが大事なところです。

