｢もとになるもの」については、しっかり意識付けをしていく【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #3】

前回（ここをクリック）は、志田倫明先生に２学年の指導内容について具体的なポイントを説明していただきましたが、今回からは、３学年の内容について具体的な指導方法を２週に分けて説明をしていただきます。

３学年では、分割分数、量分数、単位分数を学習する

３学年の分数の学習について学習指導要領解説には、｢分数とその表し方に関わる数学的活動を通して、次の事項を身に付けることができるよう指導する（p152）」とあり、次の３つの知識・技能が示されています。
（ア）等分してできる部分の大きさや端数部分の大きさを表すのに分数を用いることを知ること。また、分数の表し方について知ること。
（イ）分数が単位分数の幾つ分かで表すことができることを知ること。
（ウ）簡単な場合について、分数の加法及び減法の意味について理解し、それらの計算ができることを知ること。
まず（ア）では、等分してできる部分の大きさについては２学年の素地指導でも学習しており、端数部分というところがポイントになります｡（イ）は単位分数のいくつ分かで表すということで、初回に分数の用い方による５分類の中の３つ目、単位分数のいくつ分について学習します｡（ウ）では簡単な場合について、分数の加法及び減法の意味や計算の学習をします。３学年の分数では、これら３つのポイントを押さえていくことが大事で、これらは初回に説明した分数の表現形式の意味で言えば、第一義「１を○等分したいくつ分」に当たります。
この第一義を学ぶために、３学年では用い方による５分類の中の①分割分数、②量分数、③単位分数を学習することになっており（学習指導要領解説p153）、それぞれが用いられる場面を通して第一義（１を○等分したいくつ分）を学んでいきます。それでは、これら（ア）（イ）（ウ）の３つのポイントに沿って授業づくりについて説明をしていくことにしましょう。

｢ちょっとを数値で表したらどうなるだろう？」と考えさせる

まずは（ア）の端数部分の大きさを表すということですが、これが子供たちにはなかなか捉えにくいところで、ここを大事に扱うところが大切なポイントです。端数処理の場面設定というのは、整数では処理できない数の世界があることを教えるということです。そして、測定すると端数が生じるので、その端数部分を数値化するということを通して学習していきます。

教材としては長さや液量を扱いながら学ぶことが多いのですが、私なら４種類のコップに入っている水の量の比較を問題場面として扱います（資料１参照）。この４つのコップの中で、Ｂのコップの水は１dLマスに移すと、ちょうどぴったり１dL入っていると設定します。そこで少し水の量が少ないＡのコップを見せ、｢量はどのくらい？」と問いかけると、子供たちは隣に並んでいる１dLよりも量が少ないため、具体的には「ちょっと足りない」などと言うでしょう。この「ちょっと」が端数部分なのですが、｢何に対して、ちょっと足りないの？」と問い返すと、｢１dLに『ちょっと』足りない」と言います（資料２参照）。

【資料１】

【資料２】

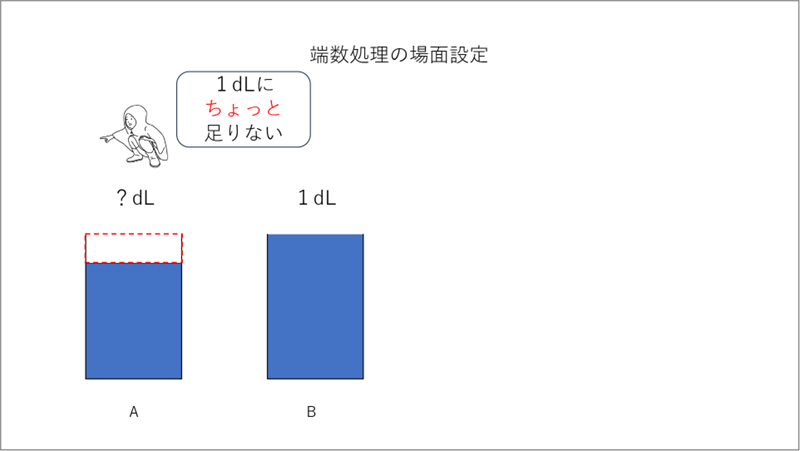
この「ちょっと」＝端数部分について、｢ちょっと、って、どれくらいだろう？」と、どのように数値化するのかについて問いかけるのです。すると子供たちは、２年生のときに折り紙を等分しながら考えていった経験がありますから、その経験とつなげて、示したdLマスの図を折ったり重ねたりしながら、「ピッタリ５等分だ」と言い出します。１dLを５等分したものですから、この端数部分は、[MATH]\(\frac{1}{5}\)[/MATH]dLだということが明らかになるわけです。子供たちが「１dLにちょっと足りない」と言っていたものが、「１dLに[MATH]\(\frac{1}{5}\)[/MATH]dL足りない」ことが分かりましたから、このコップに入った液量は「[MATH]\(\frac{1}{5}\)[/MATH]dLの４つ分だから[MATH]\(\frac{4}{5}\)[/MATH]dLだ」「あと[MATH]\(\frac{1}{5}\)[/MATH]dLあれば１dLになったのに」などと表現できるように変わっていきます（資料３参照）。

【資料３】

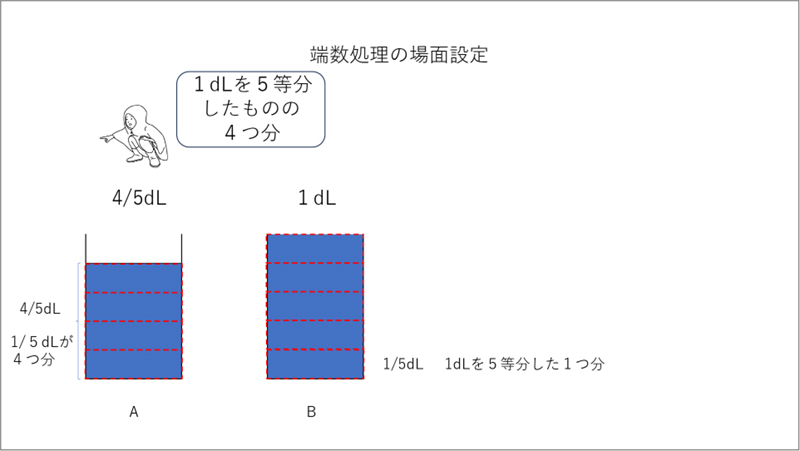
このように子供たちから「ちょっと足りない」といった言葉をうまく引き出して、｢そのちょっとを数値で表したらどうなるだろう？」と考えさせるのが、端数処理場面の設定なのです。こうした場面設定を使って先ほどのように、｢１dLにちょっと足りない」→「１dLを５等分したものの１つ分足りない」→「１dLに[MATH]\(\frac{1}{5}\)[/MATH]dL足りない」→「[MATH]\(\frac{1}{5}\)[/MATH]dLの４つ分入っている」→「液量は[MATH]\(\frac{4}{5}\)[/MATH]dL」と考え、表現できるように指導していきます。このように端数処理場面を扱うことによって、単位分数の用い方を見い出したり、単位分数のいくつ分という用い方をしたりして、（イ）についての学習もしているわけです。

３学年の分数の学習の特徴は量を扱うということ

今度は、１dLよりも液量が多いコップＣについて見てみると、｢１dLよりも少し多い」などと言います（資料４参照）。では、この端数をどう数値化するか考えると、子供たちは先ほどの経験を基に図を折り重ね、比較的短時間で「１dLを３等分したものの１つ分で[MATH]\(\frac{1}{3}\)[/MATH]dL」と考えていくでしょう。ちなみに、コップＣの液量としては１dLと[MATH]\(\frac{1}{3}\)[/MATH]dLとなり、１を超える分数（過分数、帯分数）で４年生の内容になるのですが、ここではあくまで「ちょっと」や「少し」の量をどう数値化するかを考える対象にしていきます。そのため先の例も今回も、隣にもとになる単位量１dLのコップＢを置いておくわけです。

【資料４】

このように、｢ちょっと」や「少し」を「５等分したものの１つ分で[MATH]\(\frac{1}{5}\)[/MATH]」や「３等分したものの１つ分で[MATH]\(\frac{1}{3}\)[/MATH]」といった表現形式に変えていくことで、分数の表現形式の第一義「１を○等分したいくつ分」を学んでいきます。

さらに、次学年以降の学習内容に少しだけ踏みこむ指導になるのですが、２dLのコップＤを用意しておくと、子供たちは「１dLの２倍だから２dL」と表現します。それに沿ってコップＡの液量は「１dLの[MATH]\(\frac{4}{5}\)[/MATH]だから[MATH]\(\frac{4}{5}\)[/MATH]dL」と割合的な表現に触れることもできます。また、コップＣは１dLと[MATH]\(\frac{1}{3}\)[/MATH]dLですが、[MATH]\(\frac{1}{3}\)[/MATH]dL増えると、１dLと[MATH]\(\frac{2}{3}\)[/MATH]dLとなり、さらに増えると「１dLと[MATH]\(\frac{3}{3}\)[/MATH]dLで、[MATH]\(\frac{3}{3}\)[/MATH]dLは１dLだから２dLになる」と量が増えていく感覚も話題にすることができます（資料５参照）。

【資料５】

３学年の分数の学習の特徴は量を扱うということです。１dLや１Ｌ、１mという普遍単位の付く量分数を扱うわけです。２年生の学習では折り紙やケーキなど「もとになるもの」に、様々な大きさがあるものを対象に考えました。それに対して、普遍単位であれば世界共通で、｢もとになるもの」の量が定まっているというのが教材のポイントです。

ちなみに教科書では、もとになるものよりも「ちょっと」多いもの（先の例ではコップＣ）、｢ちょっと」長いものを扱う場合が多いと思いますが、「もとになるもの」については学年が変わってもずっと貫くポイントなので、しっかり意識付けをしていくことが大切です。そのため私は、もとになるコップＢ（１dLという普遍単位）よりも「ちょっと」少ないコップＡや、「少し」多いコップＣ、ちょうど２倍のコップＤを扱うようにしています。このように複数の対象を扱って一般的な理解に引き上げていくことが大切だと思います。

端数処理場面の学習は、液量のほかに長さを扱う実践も見られますが、場面や数値の設定で子供の反応は大きく変わるので、注意が必要です。例えば、１Ｌや１mを基にして[MATH]\(\frac{1}{5}\)[/MATH]に当たる端数を考えさせると、下位単位であるdLや㎝をもち出して「２dL」や「20㎝」と表現する子供が出ることが想定されます。そのため、今回ご紹介した実践では下位単位をもち出しにくいdLを単位とした場面を設定しました。場面や数値の設定次第で想定される子供の思考を、どのように学習に位置付けるか、構想しておく必要があるのです。

執筆／教育ジャーナリスト・矢ノ浦勝之

つまずきなしの「分数」指導法
■子供たちが自ら数直線やテープ図をつくり、縦に見比べていくような学習を行う【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #5】
■単位分数を変えながら数直線づくりをし、分数も数であると意識させる【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #4】
■｢もとになるもの」については、しっかり意識付けをしていく【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #3】
■２年では、もとの大きさと部分の大きさを常に意識しながら指導 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #2】
■分数の５つの用い方を理解しておく 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #1】