２年では、もとの大きさと部分の大きさを常に意識しながら指導【｢系統」を見通し、学年ごとに押さえる！つまずきなしの「分数」指導法 #2】

2024.01.25

２年生の分数の学習は３学年以降の学習の素地をつくる

前回（ここをクリック）、各学年の指導内容について概説した通り、今回、説明していく２年生の分数の学習は３学年以降の学習の素地をつくるということで、学習指導要領には「[MATH]\(\frac{1}{2}\)[/MATH]や[MATH]\(\frac{1}{3}\)[/MATH]など簡単な分数について知ること」と記されています。なぜ簡単な分数にとどめているかというと、学習指導要領解説（p106）に「[MATH]\(\frac{1}{2}\)[/MATH]、[MATH]\(\frac{1}{3}\)[/MATH]、[MATH]\(\frac{1}{4}\)[/MATH]のように、具体物を操作することによって得られる大きさを表した、分母が１桁程度の単位分数のことである」とあるように、具体物の操作を通して分数を知ることが大きなねらいだからです。

さらに学習指導要領解説では、現行から12個のおはじきが示され、除法と乗法の素地についても触れていくことが示されています（資料１参照）。

【資料１】学習指導要領算数編解説（p107より抜粋）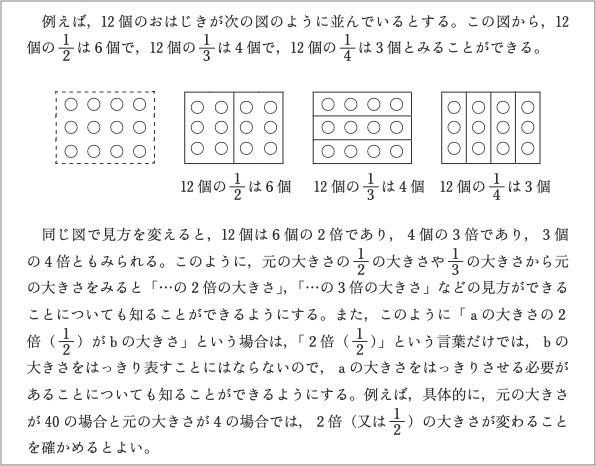

この解説からも分かる通り、２学年の指導のポイントは子供の具体的な活動を通して簡単な分数を知ることにあります。例えば、後で紹介するような折り紙を等分するような活動がそれに当たります。このような活動によって、｢折り紙を半分にしたときの１つ分を[MATH]\(\frac{1}{2}\)[/MATH]」のように、分数を用いる場面を通して分数を知ることができるようになります。このとき、「折り紙を半分にする操作を[MATH]\(\frac{1}{2}\)[/MATH]」と「操作」に注目した用い方が操作分数であり、「折り紙を半分にしたときの１つ分を[MATH]\(\frac{1}{2}\)[/MATH]」のように等分し終わった「結果」に注目した用い方を分割分数と言います。

さらに、この解説の記述の最後にもある通り、２学年の指導のポイントとなるのは、もとの大きさの１が変わると同じ[MATH]\(\frac{1}{2}\)[/MATH]でも大きさが変わるということの理解です。つまりもとの大きさと部分の大きさを常に意識しながら指導をしていくことが重要になります。

そもそも分数は（前回ご説明したように）有理数の表現形式の一つであり、子供たちにとっては「数」です。では分数の学習に入るまで、子供たちが数をどのように学んできたかというと、１年生の教科書を見ると分かる通り、クマも切り株もブロックもすべて１つあれば１です。大きさや物や色や形を捨象して、｢１匹、２匹、３匹…」｢１個、２個、３個…」と数詞で数えていくことに対応して数を学んできました。ですから、アリも１匹ですし、ゾウも１頭であり、２ついればアリも２匹、ゾウも２頭となります。これが操作による理解で、子供は操作を通して１、２という量として判断して数を学んできているのです。

もとになる「１」が同じであれば、分け方は違っても「[MATH]\(\frac{1}{2}\)[/MATH]」は同じ大きさ

さて、具体的な２学年の分数指導の内容に入っていくことにしましょう。
分数の学習では折り紙を使って学ぶことが多いと思います。折り紙を半分に折ってピッタリ重なって半分になったものを[MATH]\(\frac{1}{2}\)[/MATH]だと学んでいくわけですが、このときに、本当に子供が[MATH]\(\frac{1}{2}\)[/MATH]を量として捉えているのかというところがむずかしいところです。もしかしたら、形としてしか捉えていないかもしれません。縦に折ってできた２つの長方形は重ねればピッタリ重なりますし、斜めに折ってできた直角二等辺三角形もピッタリ重ね合わせることができますから、同じ量で[MATH]\(\frac{1}{2}\)[/MATH]と授業でも確認することができるでしょう（資料２参照）。

【資料２】

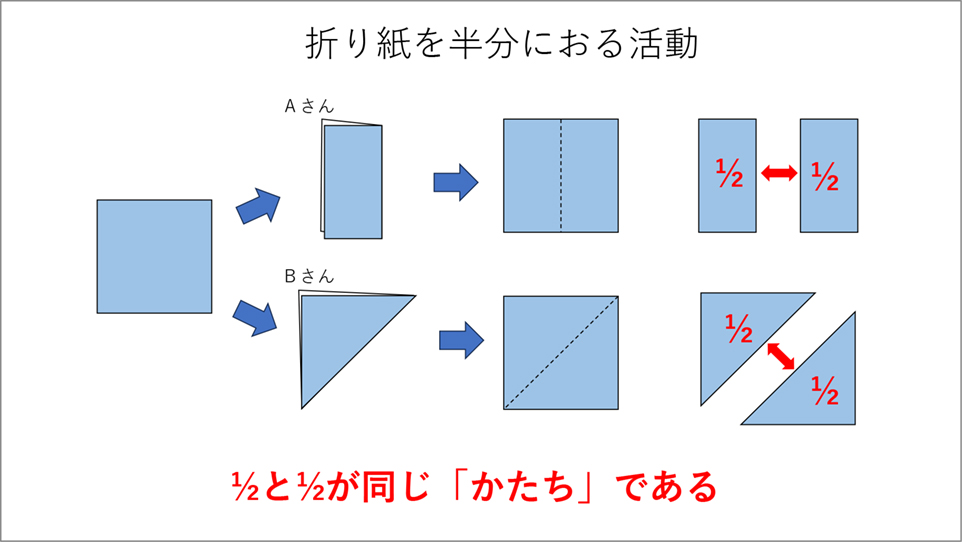
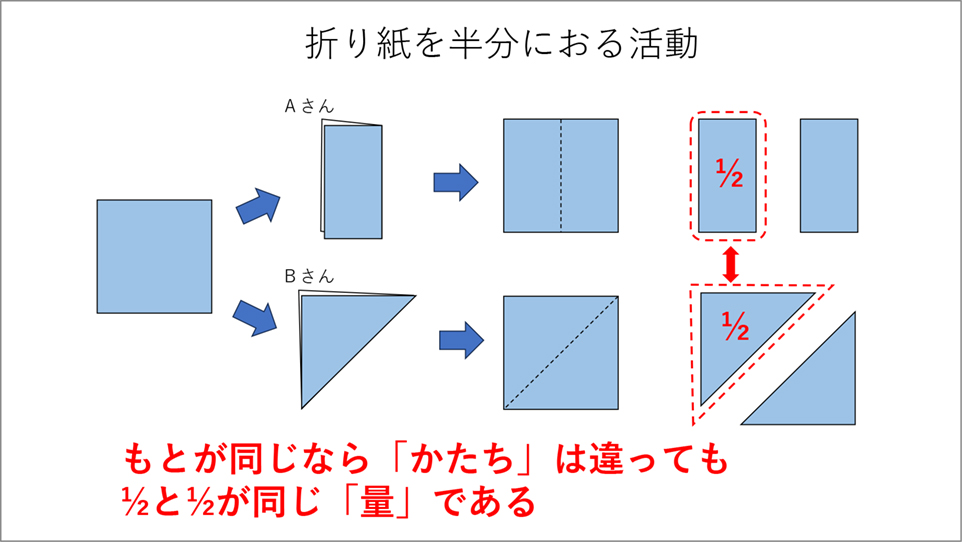
しかし、この長方形と直角二等辺三角形はそれぞれ形が同じだから（重なるから）、同じ量で[MATH]\(\frac{1}{2}\)[/MATH]と捉えている子供もいるかもしれません。それについて子供たちに問いかけ、一緒に考えてみることが大切です。「折り紙を縦に折ったＡさんと斜めに折ったＢさんは同じ大きさと言っていいのかな？」と問うと、実際に「形が違うから同じではない」「重ならないから同じではない」といった意見が出てくるかもしれません。しかし、対話を通しながら、異なる図形の一部分を切って変形などして説明し、最終的には「もとになる同じ大きさの折り紙を２つに分けた１つ分だから（長方形も直角二等辺三角形も）どちらも同じ大きさだよ」ということが理解できるはずです（資料３参照）。

【資料３】

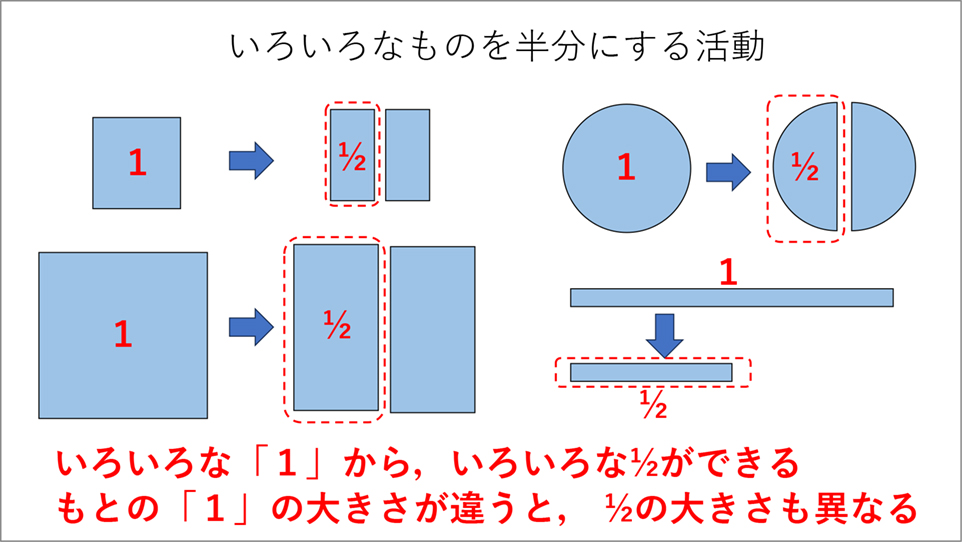
それが理解できたら、もとの大きさの異なる大小の正方形、円や長方形など形の異なる図形を使って学習していけば、いろいろな形や大きさの１から[MATH]\(\frac{1}{2}\)[/MATH]ができることを体験し、さらに同じ[MATH]\(\frac{1}{2}\)[/MATH]でも、もとになる大きさが異なれば「量」として異なることを感じ始めていくことでしょう（資料４参照）。

【資料４】

もとになる「１」の大きさが変わると、同じ「[MATH]\(\frac{1}{2}\)[/MATH]」でも数（＝量）が変わる

ここから、｢イチゴが12個のっているケーキを同じ大きさに切る」というような学習をしていきます。これは、先に紹介をした学習指導要領解説にある除法と乗法の素地指導につながっていくものです（資料１の図参照）。しかし、このときすぐに[MATH]\(\frac{1}{2}\)[/MATH]、[MATH]\(\frac{1}{3}\)[/MATH]、[MATH]\(\frac{1}{4}\)[/MATH]に切り分ける学習に入っていくのではなく、意図的にもとになる大きさが異なり、18個のイチゴがのっている大きなケーキを設定し、それぞれを２つに切るような学習を入れてみるとよいでしょう。そうすることによって、もとになる「１」の大きさが変わると、同じ「[MATH]\(\frac{1}{2}\)[/MATH]」でも数（＝量）が変わる、という気付きがより確かな理解になっていくはずです。

その上で12を２等分、３等分、４等分していく学習を進め、12を２等分すれば６と６に分けられ、12を３等分すると４と４と４、12を４等分すると３と３と３と３ということを操作を通しながら、すでに学習した「かけ算に似ている」ということを実感していく、除法や乗法の素地指導を行っていくとよいでしょう。

12個のマス目からなる長方形をもとにした問題に取り組む

これまで説明してきたような学習を通して、もとの大きさの１が変わると、同じ[MATH]\(\frac{1}{2}\)[/MATH]（や[MATH]\(\frac{1}{3}\)[/MATH]、[MATH]\(\frac{1}{4}\)[/MATH]）でも大きさが変わるということ、もとの大きさが同じであれば[MATH]\(\frac{1}{2}\)[/MATH]（や[MATH]\(\frac{1}{3}\)[/MATH]、[MATH]\(\frac{1}{4}\)[/MATH]）も同じで、形などに左右されないということがしっかり理解できれば、子供たちにとって楽しい発展的な学習をしていくことも可能になります。

これは実際に私のクラスで行った授業ですが、12個のマス目からなる長方形をもとにして、｢どんな[MATH]\(\frac{1}{□}\)[/MATH]があるかな」という問題に取り組みました。子供たちはすでに形に捉われずに考えられるようになっているので、例えば[MATH]\(\frac{1}{3}\)[/MATH]も、異なるテトリスのブロックのようなものを使って考えていきます（画像参照）。やがて、マス目を斜めに切って変形する子供も出てくるなど、本当に楽しい学習ができました。

やはり、２学年の分数の学習では、もとになるものは何か、もとになるものが変われば部分（等分したもの）の大きさが変わるということを子供たちが意識して学習していくようにすることが大事です。それができていれば、もとが２mになったら[MATH]\(\frac{1}{3}\)[/MATH]は何mか（前回紹介した全国学力調査の問題）といった、３学年以降の内容にもスムーズに入っていくことができると思います。