小２算数「三角形と四角形」指導アイデア《三角形、四角形についての理解を確実にする》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2023.12.19

単元の展開

第１時　三角形や四角形のパズルを使って、例示されている図形をつくること。
▼
第２時　辺や頂点の数に着目して図形を分類する活動を通して、三角形、四角形の意味や性質を理解すること。
▼
第３時（本時）図形を弁別する活動などを通して、三角形、四角形についての理解を確実にすること。
▼
第４時　直角の意味を知り、身の回りから直角を見付けることができること。
▼
第５時　長方形を構成要素に着目して見ることを通して、長方形の意味や性質を理解すること。
▼
第６時　正方形を構成要素に着目して見ることを通して、正方形の意味や性質を理解すること。
▼
第７時　長方形、正方形を対角線で分割してできた三角形を、構成要素に着目して見ることを通して、直角三角形の意味や性質を理解すること。
▼
第８時　方眼を利用した長方形、正方形、直角三角形のかき方を、方眼の仕組みや図形の性質に着目して考え、作図することができること。
▼
第９時　身の回りから長方形や正方形を探したり、敷き詰め模様をつくったりする活動を通して、問題を解こうとすること。
▼
第10時　学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り、価値付けること。

本時のねらい

図形を弁別する活動などを通して、三角形、四角形について理解することができる。

評価規準

三角形や四角形の約束を基にいろいろな図形を弁別し、説明している。

本時の展開

前回どんなことを学習しましたか。

三角形と四角形です。

三角形と四角形の約束は何でしたか。

三角形は、３本の直線で囲まれた形。四角形は、４本の直線で囲まれた形です。

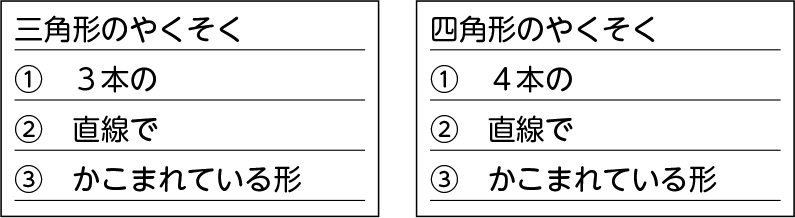
２つの約束は「直線で囲まれている」というところが似ているよね。

アからキまでの形をなかま分けしよう。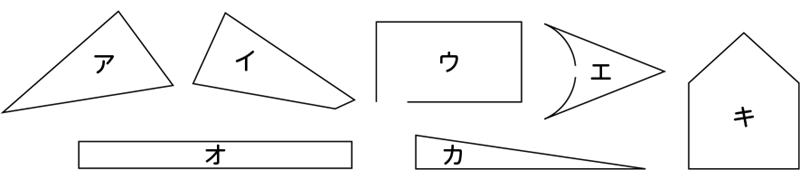

今日はいろいろな形を持ってきました。

うわー。たくさん図形があるね。

この形（ア）は何ですか。

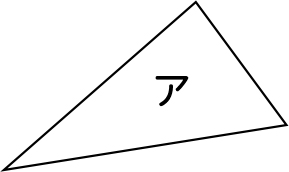
三角形です。

なぜ三角形なのか説明できますか。

辺が３本だからです。　　

頂点が３つだからです。　

３本の直線で囲まれている形だからです。

いろいろな説明が出てきました。そうですね。３本の直線で囲まれているから三角形と言えますね。では、次の形（イ）は何と言いますか。

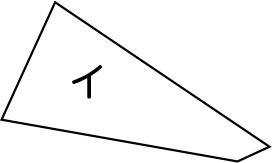
三角形です。　

四角形です。

あれ、分かれましたね。わけを説明できますか。

見た目が三角形なので、三角形だと思います。　

だけど、辺の数と頂点の数は「４」じゃないかな。三角形は「３」だったけれど……。

ほかにはどうでしょう。

見た目が三角形だけど、４本の直線で囲まれている形だから四角形だと思います。

ほかの形も見ていきましょう。この形（ウ）は何でしょう。

直線が４本あるので、四角形だと思います。

でも、見た目は四角形だけど、穴が空いているよ。

直線で囲まれているのが約束なんだから、三角形でも四角形でもないと思います。

確かに、｢直線で囲まれている」のが約束だったので、三角形でも四角形でもどちらの仲間にもならない形もあるんですね。ほかにもいろいろ形を持って来ましたが、今日はどんな学習ができそうですか。

先生が持ってきた形を仲間分けしてみたいです。

では、これらの図形を仲間分けしてみましょう。仲間の分け方の理由も説明しましょう。

図形を、「①三角形」「②四角形」「③どちらでもない形」の仲間に分け、分けた理由も説明しよう。

見通し

見た目で３つの仲間に分けることはできそうだけど、理由は何と書こうかな。

三角形と四角形ではない形には少しおかしいところがあるから、そこを理由として書こう。

昨日学習した形の約束を使えば、全部の形の仲間分けの理由を説明できそうだ。

自力解決の様子

Ａ　つまずいている子
・見た目で判断し、根拠を説明することができない。
①ア・イ・エ・カ
②ウ・オ
③キ

Ｂ　素朴に解いている子
・図形を構成する要素（辺や頂点の数）に着目し、仲間分けしている。
・見た目からエを「どちらでもない形」と判断している。
①ア・カ
②イ・オ
③ウ・エ・キ

Ｃ　ねらい通り解いている子
・三角形と四角形の約束を基に、図形の仲間分けのしかたについて説明している。
・イについても、四角形の約束を基に「四角形」と判断している。
①ア・カ
②イ・オ
③ウ・エ・キ

学び合いの計画

学び合いの時間では、Ａの子供のような見た目から判断をしている考え方、Ｂの子供のように図形を構成する要素に着目したり、主観的な判断から説明したりしている考え方、Ｃの子供のように三角形や四角形の約束を基に、すべての図形について一貫性のある説明をしている考え方を比較し、能率的に処理することのよさに気付けることが重要です。

まず、三角形（ア・カ）と四角形（イ・オ）など、比較的理解しやすい図形を確認します。そして、意見が分かれそうな図形の話し合う時間を充実させます。

また、Ａの子供も「③どちらでもない形」と判断した理由の説明は書けていなくても、判断した箇所はあるはずです。どこがおかしいと思ったのか発表し、そこの説明をＢ、Ｃの子供がしていき学級全体で学び合いを深めていけることが大切です。

ウの図形を例にすると、Ｂの素朴に考えている子は、辺と辺がつながっていないところがある、角が１つできていない、頂点が３つしかできていないなど、多様な考えが出てくると思われます。エも同様に、１つの辺の線が曲がっている、カーブしているという考えが出てくると思われます。

それらの考えをていねいに取り上げ、辺と辺がつながっていない、角ができていないのはどうしてなのか考えていき、導入で示した三角形と四角形の約束を基に仲間分けの判断ができるようにしていくことが重要です。

その際、板書に示している約束を指しながら確認していき、ウやエのように１つでも条件を満たさなかった場合は三角形や四角形のどちらでもないことを理解できるようにします。

このように一般化することができたら、イの図形について改めて考察する時間を取ります。約束を基に仲間分けをしても、見た目から「やはり三角形に見える」と捉える子供がいることが予想されます。

そこで再度四角形の約束をふり返り、４本の直線で囲まれている、頂点や角が４つあるなど約束をすべて満たしているため、四角形の仲間に入ることを確認します。

そして、Ｃの子供のようにすべての図形で三角形と四角形の約束に基づいて一貫性のある説明をしている子供を取り上げ、簡潔、明瞭、的確に表現できていることを評価します。

また、キの図形も三角形と四角形の仲間には入らないが、何と言う図形になるか予想したり、ウやエをどのようにしたら三角形・四角形になるか問うたりすることで、発展的な見方ができるようにしていきます。