【教科調査官に聞く】算数科の新学習指導要領－改訂ポイントと授業改善の視点

学習指導要領の改訂にあたり、そのポイントや授業改善の視点などをテーマに、文部科学省・笠井健一教科調査官と、東京都公立小学校・増本敦子教諭に対談していただきました。

増本敦子（ますもとあつこ）［右］：小学校学習指導要領（平成29年告示）解説算数編、作成協力者。第100回全国算数・数学教育研究（東京）大会シンポジウム【幼稚園・小学校部会】シンポジスト。朝日新聞「花まる先生」掲載、NHK「さんすう犬ワン」番組企画協力、算数の雑誌、教育雑誌等の執筆多数。

笠井健一（かさいけんいち）［左］：文部科学省初等中等教育局 教育課程課教科調査、国立教育政策研究所、教育課程研究センター研究開発部、教育課程調査官・学力調査官。東京学芸大学教育学部附属小金井小学校教諭、公立小学校教諭、主幹を経て、2007年より山形大学地域教育文化学部講師、同大学大学院教育学研究科講師、2008年より現職。主な編著書に『小学校算数 アクティブ・ラーニングを目指した授業展開』（東洋館出版社）。

改訂のポイントは五つ　数学的活動を意識しよう

増本　小学校の学習指導要領の算数科の改訂のポイントについて、教えてください。

笠井　改訂のポイントは五つあります。

一つめは、算数科で育成を目指す資質・能力を明確にするために、目標及び内容を資質・能力の三つの柱で整理しました。これは算数科だけではなく、すべての教科等の改訂のポイントになります。

算数科　目標
数学的な見方・考え方を働かせ、数学的活動を通して、数学的に考える資質・能力を次のとおり育成することを目指す。
1.数量や図形などについての基礎的・基本的な概念や性質などを理解するとともに、日常の事象を数理的に処理する技能を身に付けるようにする。
2.日常の事象を数理的に捉え見通しをもち筋道を立てて考察する力、基礎的・基本的な数量や図形の性質などを見いだし統合的・発展的に考察する力、数学的な表現を用いて事象を簡潔・明瞭・的確に表したり目的に応じて柔軟に表したりする力を養う。
3.数学的活動の楽しさや数学のよさに気付き、学習を振り返ってよりよく問題解決しようとする態度、算数で学んだことを生活や学習に活用しようとする態度を養う。

特に身に付けてほしいことを、知識及び技能と思考力・判断力・表現力等との両方明示したことが大きなポイントです。「計算できればよい」など知識及び技能だけではなく、計算の意味や仕方を考えたりすることなどが思考力・判断力・表現力等に示されているので、そのねらいに沿った授業が求められます。

二つめは、数学的活動の一層の充実です。今回、算数的活動から数学的活動に言い換えました。これは、下の図Aを基に、小・中・高等学校を系統立てて算数・数学の活動を整理し、小・中が一貫して同様な数学的活動が行われるようにしました。小学校算数の数学的活動は、図A左の「日常の事象から見いだした問題を解決する活動」と、図A右の「算数の学習場面から見いだした問題を解決する活動」という二つが中心としてあり、「数学的に表現し伝え合う活動」がその二つに関わっています。それに、小学校独自の「数量や図形を見いだし、進んで関わる活動」を入れて、数学的活動を整理したわけです。

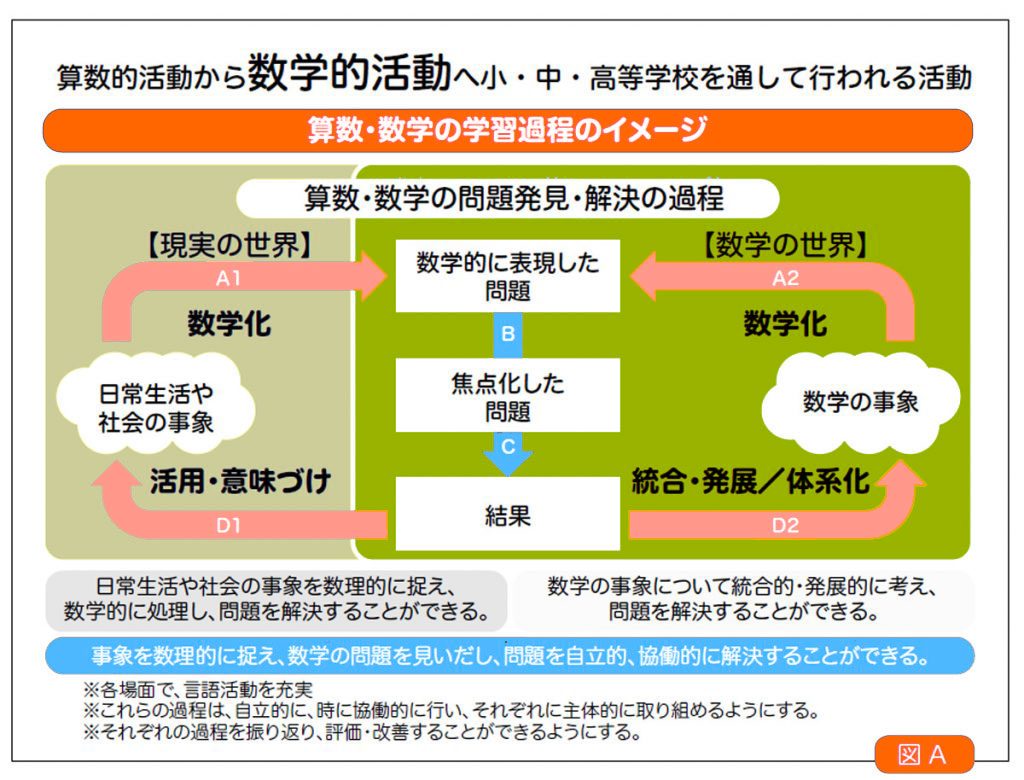
例えば、たし算だったら、「最初の日はどんぐりを8個拾って、次の日は3個拾いました。全部で何個になりましたか」という問題は、どんぐりという子供たちの身近な日常の事象で「現実の世界」です。そして、8＋3の計算の仕方を考えるという問題が焦点化されます。さらに、8＋3だけではなく、8＋4や8＋5をやってみようという時に、今度は右側のサイクル「数学の世界」に入っていきます。この両方のサイクルがあることを意識することが大事です。

三つめは、数学的な見方・考え方や育成する資質・能力に基づき、領域の構成を見直しました。領域については、現行の学習指導要領では、特に数量関係の中に、異なる内容が入っていましたが、それを整理して、どんな内容かをひとことで言えるようにしました。「数学的な見方・考え方」はこれまで使ってきた「数学的考え方」と言葉が似ているのですが、捉え方が違います。今までの数学的考え方は、思考力・判断力・表現力の評価の観点名で、数学的考え方を評価するものでした。今回の数学的な見方・考え方は、「事象を、数量や図形及びそれらの関係などに着目して捉え、根拠を基に筋道を立てて考え、統合的・発展的に考えること」としています。つまり、評価するものではなく、問題を解決する場面で、「数学的な見方・考え方」を働かせるものと捉えています。

例えば、量には長さ・かさ・広さがあります。長さを比べる時には長さに、広さを比べる時には広さに、かさを比べる時にはかさに着目しないといけません。何を比べたいかということを、はっきりとわかっていることが大切です。これは新しいことではなく、今までも大切にしてきたことなので、それを言葉でまとめたわけです。

四つめは、割合に関する内容を充実、五つめは統計に関する内容を充実しました。

割合、統計を充実

増本　割合に関する内容が充実されました。四年生には簡単な割合が新設されましたが、割合の充実について教えてください。

笠井　割合については、今まで、五年生で「百分率を理解する」という表現で示されていました。今回、五年生の割合については「百分率を用いた表し方を理解し、割合などを求めること。」という内容に加え、「ある二つの数量の関係と別の二つの数量の関係とを比べる場合に割合を用いる場合があることを理解すること。」という内容が入ります。五年生では小数で比べる学習になります。その前段階として四年生の内容に、「簡単な場合について、ある二つの数量の関係と別の二つの数量の関係を比べる場合に割合を用いる場合があることを知ること。」という整数で比べるという簡単な割合が入りました。

増本　次に、データの活用の領域が新設され、統計の内容が充実されました。今までの統計の学習とどう変わるのでしょうか。

笠井　現行では、あるデータが与えられ、それをグラフに表し、グラフからわかることを分析するという学習が主だったのですが、今回、五年生のデータの活用に「データの収集や適切な手法の選択など統計的な問題解決方法を知ること。」ということが新たに入っています。

つまり、身の回りの問題から、どのようなデータを集めたらよいのか計画を立て、目的に応じてデータを集めて分類整理し、データの特徴や傾向に着目し、問題を解決するために適切なグラフを選択して判断し、その結論について多面的に捉え考察できる子供になってほしいと思って新設しました。例えば、児童会のあいさつ運動の成果や保健委員会のハンカチ調査などの場面が考えられると思います。

また、二つの集団を比べる時に、平均値で比べることが多いのですが、中央値や最頻値で比べたほうがよい場合があります。これまで中学一年生で学習している中央値や最頻値を小学六年生で学習し、二つの集団を比べる時に、どの値で比べたほうがよいのか、子供たち自身が判断できるようになってほしいということで「中央値」「最頻値」を入れています。

算数科の「主体的・対話的で深い学び」とは

増本　全国の学校を訪れて、現場での状況はいかがですか。

笠井　学習指導要領が告示される前から中央審議会などで「主体的・対話的で深い学び」がキーワードとして出されていましたので、「主体的・対話的で深い学び」を研究主題にするなど、新しい学習指導要領に興味をもって取り組んでいる学校が多いと感じています。「主体的・対話的で深い学び」といった時に、算数の授業の場合、最初の問題の場面に、生活科で扱うあさがおや人気キャラクターなど日常の場面を設定して、子供たちがその問題を解いてみたいという気持ちにさせる取組をよく拝見します。

それはとてもよいことですが、子供たちが問題を解いて、うまくいかなかったから考えなくなってしまうのでは、主体的とはいえません。粘り強く取り組めるように工夫することが大切で、そのときにポイントになるのが、見通しをもたせることです。

そして、自らの学習活動を振り返って、次につなげることが大事です。例えば、8＋3が11になったことをまとめにすると、他の数での応用が利きません。そこで、8＋3のときには、3を2と1に分けるとよかったことをもとに、8にたすときは10に対する補数の2をたすことをまとめにするといいと思います。そうすれば、さらに9や7ならどうなるかと、次につなげることができます。そして、このように振り返ったことをノートに簡潔に図にかいて残しておくと、次の時に見直すことができます。主体的な学びでは、日常的な場面を設定することだけではなく、見通しをもたせたり、振り返りをしたりすることが重要になります。

対話的で深い学び

増本　対話的な学びでは、どのようなことを大切にするとよいのでしょうか。

笠井　対話的な学びには、ペア学習、グループ学習、学級全体で学び合いをすることなどが考えられます。どれがよいのかは、その時の子供たちの様子によって変えていくことが大切です。大事なのは、聞き手を育てることです。つまり、自分は答えが出たから「もういいや」というのではなく、自分よりもっとよい方法があるから、友達の考えを聞きたいという子供を育て、友達の考えをうなづきながら聞き、わからない時は、わからないことを聞けるようにすることが大事なのです。

教師の留意点としては、得意な子供が発表し、苦手な子供が聞くという対話的な学びではなく、苦手な子供がここまで考え、ここから先がわからないので教えてほしいという、そこから説明する方が、対話的な学びは効果的になるでしょう。子供たちが自分の考えを広げたり、深めたりできるようにすることが最も重要な点です。

増本　深い学びについては、いかがでしょう。

笠井　深い学びというと、一般的にはチャレンジ問題や発展問題を授業の終わりにして、それができたから深い学びだと思われているようですが、それができることは、深い学びの一つではあります。しかし、一年生にとっての深い学びは、今日教えたいことがきちんと身に付く。最初わからなかったことが、きちんとできて、みんなができる。それを目指すことが、最初にしてほしい深い学びの姿だと思います。

8＋3は、11と答えられる子が深い学びというのではなく、計算の仕方がわかるというのが授業のねらいだとすると、11と答えられるだけではなくて、その方法を図でも表すことができることが深い学びの姿だと思います。深い学びの具体の姿を想定して、実際できたかどうかを見ていくことがポイントになります。

先生には、教えるべきこと、今日気付かせたいこと、子供たちの思考を深めるような、発言をうながし、気付いていない視点を提示するということを大事にして、主体的・対話的で深い学びという三つの言葉を踏まえて授業することを願っています。

この対談は、教育技術 MOOK『何が変わるの？教科等の要点が簡潔にわかる！新学習指導要領　ここがポイント』（小学館刊）からの転載です。

取材・文・撮影／浅原孝子

『教育技術 小五小六』2019年10月号より