小6算数「資料の整理（度数分布表）」指導アイデア
執筆／埼玉県公立小学校教諭・齋藤礼乃
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
（本時4／13時）
ねらい
データの散らばりを度数分布表に整理する方法を理解し、数値（度数）をもとに特徴を読み取ることができる。また、自分なりの観点をもち、資料を考察することができる。
評価規準
データを度数分布表に整理し、自分なりに観点を決め各クラスの特徴を述べることができる。
※前時ではドットプロットを扱った授業を行っているものとする。前時のドットプロットを提示する。
問題場面
学年縄跳び大会に向けて各クラスで毎日練習に取り組んだ結果を表に整理し、賞を考えましょう。
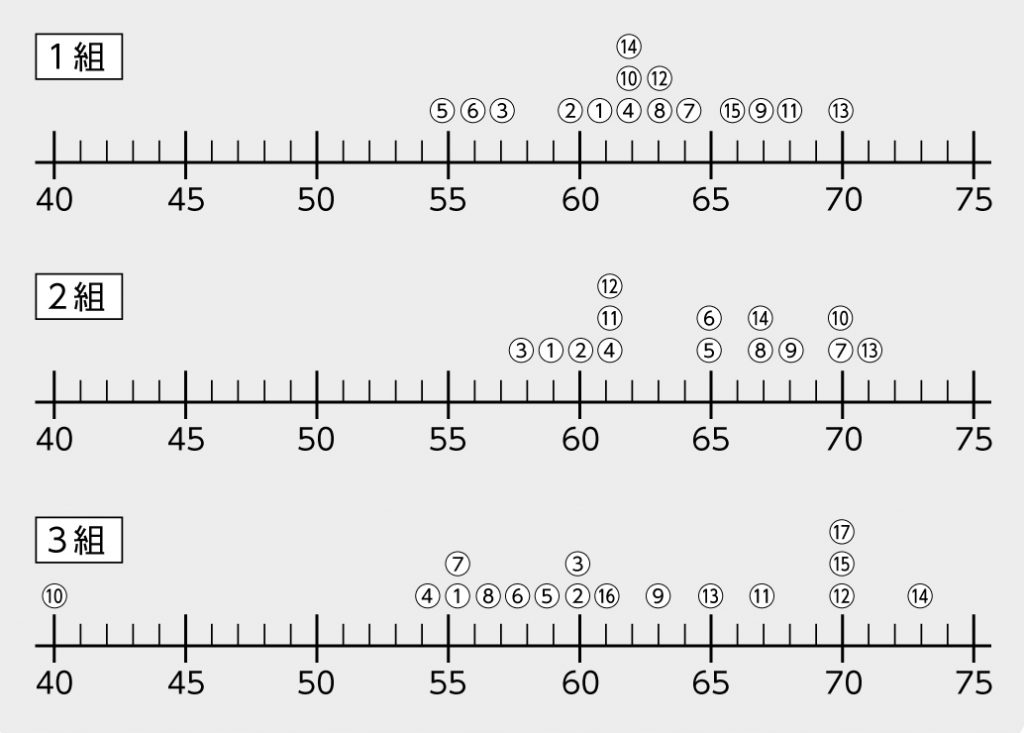
学年縄跳び大会で、練習期間を含めて各クラスに「賞」をあげることになりました。練習で跳べた回数をドットプロットに表すと、数値の散らばりに違いがありましたね。
クラスによって回数の散らばり方に違いがありました。3組では最頻値から離れている数値もありました。
回数の散らばりはあるけれど、ある程度のまとまりでまとまっていることも分かった。
ドットプロットを、表に整理するとぴったりの「賞」がつくれないかな。
回数を表に整理すると、さらに特徴が分かりやすくなりそうですね。
では本時では、回数の散らばりの様子が分かりやすいように表に整理して3つのクラスの特徴をもとに、賞をつくってみましょう。
本時の学習課題
各組の回数を表に整理し、散らばりの様子の特徴をもとに賞を考えよう。
見通し
- 一番少ない数は40回で、一番多い数が73回だから、40～73までの数が入る表が必要だね。
- 前回のドットプロットの数直線のように5（回）ずつに区切れば、ある程度のまとまりができるよ。
- 数値の大きいまとまりの日数や、回数のまとまりが占める割合で比べると、ぴったりの賞が決められるんじゃないかな。
自力解決の様子
A つまずいている子
表に数値を入れる際に、「以上」、「未満」の意味が捉えられず、正しく数値を入れることができない。また、表に整理したものの、どう比べればよいかわからない。
B ねらいどおりに解決している子
（例）「70以上75未満」の度数を見ると、2組は3日、3組は4日だから、3組のほうが好記録を出していると言えます。「スーパープレー賞」なんてどうかな。
C 進んでいる子
各組の階級ごとの数値を見ると、3組は最大の階級「70以上75未満」を4日も出しているが、「65回以上」で考えると、2組は練習日の半分以上とんでいます。でも、2組は「55回未満」の日も2日あるため、記録が安定していないと言えます。
学び合いの計画
本時では、“賞”を作る活動を通し、各組の特徴を度数分布表をもとに考察することをねらいとします。
イラスト／横井智美
『教育技術 小五小六』2021年12/1月号より
