小3算数「かけ算の筆算2けた」指導アイデア(9/9時)《線を引くだけで計算できるひみつ》

執筆/神奈川県横浜市立原小学校教諭・葛谷勲
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 1位数×何十の計算のしかた
▼
第2時 2位数×何十の計算のしかた
▼
第3時 2位数×2位数の計算のしかた(12×23)、筆算のしかた
▼
第4時 2位数×2位数の計算のしかた(58×46)、繰り上がりあり
▼
第5時 2位数×2位数の計算のしかた、乗数の末尾に0がある1位数×2位数
▼
第6・7時 3位数×2位数の計算のしかた、筆算のしかた(587×34)
▼
第8時 簡単な場合の2位数×1位数の暗算のしかた
▼
第9時(本時)十進位取り記数法及び筆算の仕組みのよさを感得する。
本時のねらい
線を引いただけで2位数×2位数の計算ができる仕組みを考えることを通して、十進位取り記数法及び筆算の仕組みのよさを感得する。
評価規準
数の構成に着目して計算したことを基に考え、説明している。
本時の展開

線を引くだけで12×23が計算できるひみつを見つけよう。
これまでかける数が2桁の筆算の計算のしかたを学んできましたね。ところで、数字を書かなくても計算することはできますか。
えっ、そんなことできるわけありません。
では、12×23の計算を数字を書かないで答えを出します。(実際に書く)
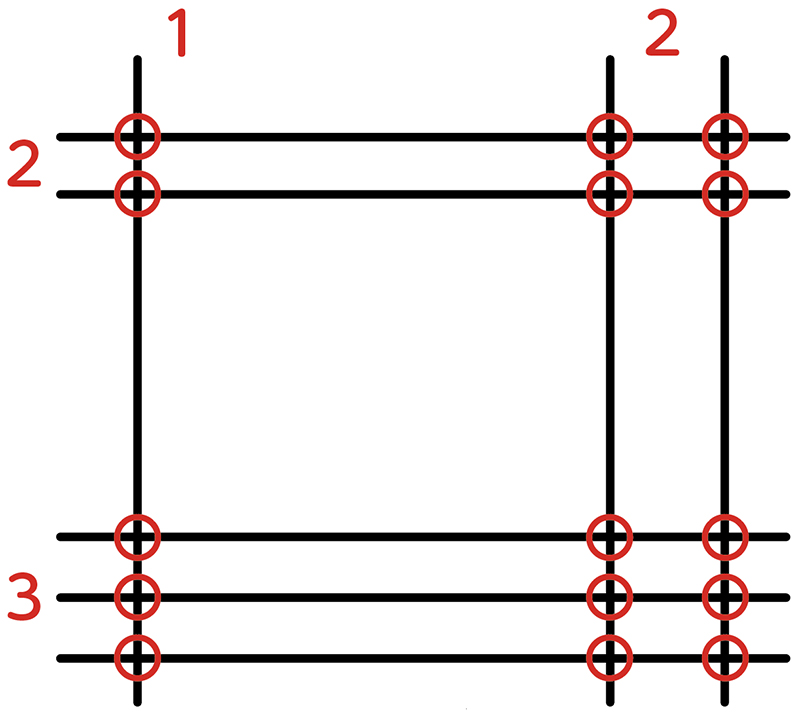
答えは、276です。合っていますか。皆さんは筆算で計算をして確かめてください。
(実際に筆算で確かめた後)すごい! 合っている!
先生、最初から答えを知っていたんでしょ。
たまたま合っていただけかもしれないじゃん。
では、違う計算もやってみましょうか。
※子供に2桁の数を決めさせて計算してみる。例えば、25×13。
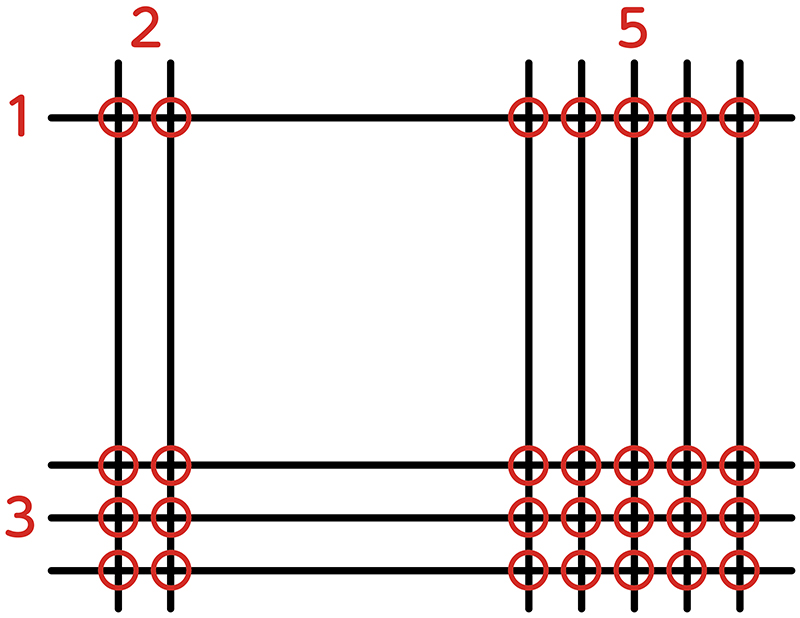
答えは、325です。合っていますか。
(実際に筆算で確かめた後)えっ、すごい! また合っている!
どうして線を引くだけで答えが分かったのでしょうか。
もしかしたら、何か「ひみつ」があるのかしれない。
では、今日は線を引くだけで答えが分かる「ひみつ」を考えましょう。

線を引くだけで積を求められる活動を通して、かけ算の筆算の性質に着目し、位ごとに計算するよさを考察する。
見通し
間をあけて線をかいているから、かける数とかけられる数を表しているんじゃないかな。(方法の見通し)
線が交わっている点にひみつがありそう。(方法の見通し)
線と線が交わっている点に注目すれば、ひみつが分かるかもしれない。(結果の見通し)
自力解決の様子
A つまずいている子
線と線が交わっている点を数えることができるが、そこで止まっている。
B 素朴に解いている子
線と線が交わっている点の数が、筆算のときに表れる数と同じことに気付くことができる。
C ねらい通り解いている子
線と線が交わっている点の数が位どうしの積になっていることに気付き、説明することができる。
学び合いの計画
かけ算の筆算は、計算の練習が必要な単元です。何度も繰り返し計算しているうちに、子供たちに飽きが見えてくるような場面もあるでしょう。桁数が多くなるにつれて、位や数が増え、煩わしく感じる子供も少なくないでしょう。
イラスト/横井智美

