小6算数「比例と反比例」指導アイデア《反比例する二つの量の変わり方と特徴》

執筆/新潟県新潟市立南万代小学校教諭・水倉祐美
監修/文部科学省教科調査官・笠井健一、新潟県新潟市立新津第一小学校校長・間嶋哲

目次
単元の展開
第1時 伴って変わる二つの数量の変わり方について考える。
▼
第2時 紙の枚数と紙の重さとの関係を調べ、説明する。
▼
第3時 針金の長さと重さの二つの数量が伴って変わることを調べ、比例の意味について考える。
▼
第4時 比例の性質について考え、比例の関係は式で表すことができることを知る。
▼
第5時 比例の性質を利用して、比例の関係を式で表す。
▼
第6時 xとyの関係を式に表し、決まった数は何を表しているか考える。
▼
第7時 比例の関係をグラフに表すことを考え、かき方と特徴を知る。
▼
第8時 グラフを見て、比例しているかどうかを判断したり、数値を読んだりする。
▼
第9・10時 比例の関係を表す式やグラフを用いて、問題解決の方法を考える。
▼
第11時(本時)反比例する二つの量の変わり方を調べ、反比例の特徴を考える。
▼
第12時 反比例の性質を見付け、反比例を表す式やグラフについて考える。
▼
第13時 反比例の性質を利用して、問題解決の方法を考える。
▼
第14・15時 適用問題を解く。
本時のねらい
反比例の意味や性質について、面積が一定のときの長方形の縦と横の長さの関係について調べる活動を通して、比例の意味や性質と比較しながら、反比例する二つの量の変わり方や対応する値の特徴を説明することができる。
評価規準
反比例の関係にある二つの数量について、比例の場合と比較しながら、二つの量の変化や対応の特徴を考え、説明することができる。
本時の展開
今からいくつか、伴って変わる二つの量が出てきます。yがxに比例しているかどうか考えましょう。

比例を見付けよう。
※フラッシュカードで一つ一つ提示する。
①1枚24円のカードx枚と代金y円
②底辺24㎝、高さx㎝、面積がy㎠の平行四辺形
③横の長さx㎝、縦の長さy㎝、面積が24㎠の長方形
簡単です。①は比例しています。
式にすると……、24×x=yです。だから、カードの枚数xが2倍、3倍……になると、代金yも2倍、3倍……になります。
本当に2倍、3倍になっていますか。
なっています。ほら、表にかくと……。
いいですね。表にかいて確かめてみましょう。
見てください。xが1枚のとき、代金yは24円。xが2枚のとき、代金yは48円。xが3枚のとき、代金yは72円。xが2倍、3倍……になると、yも2倍、3倍……になるので比例しています。
同じです。xが2枚のとき、代金yは48円。xが4枚のとき、代金yは96円。この部分も2倍になっています。表にすると分かりやすいです。
では、式で表すとどうなりますか。
24×x=yです。
同じです。だから、y=24×x。決まった数は24です。
yがxに比例するとき、二つの量の関係を式で表すと、y=決まった数×xになるのでしたね。では、②はどうですか。
②も比例しています。
同じです。だって、平行四辺形の面積は、底辺×高さで求められるから、高さが高くなると面積も大きくなっていきます。底辺xが2倍、3倍……になると、面積yも2倍、3倍……になるはずです。
でも、さっきみたいに表で確かめてみたいな。
表で確かめた結果を教えてください。
xが1㎝のとき、面積yは24㎠。xが2㎝のとき、面積yは48㎠。xが3㎝のとき、面積yは72㎠です。だから、xが2倍、3倍……になると、yも2倍、3倍……になるので比例しています。
ほかの部分でも同じことが言えますか。
言えます。この部分を見てください。xが3㎝のとき、面積yは72㎠。xが6㎝のとき、面積yは144㎠です。
やっぱり、比例しているね。式も言えます。y=24×xです。
式に表してみると、①と同じだね。
最後に、③はどうですか。
ん? あれ? 今までと違って、③は比例してないな。

面積が決まっている長方形の横の長さx㎝、縦の長さy㎝の二つの量は、どのような関係だろうか。
見通し①
面積が24㎠になる長方形は、例えばどんなものがありますか。
縦4㎝と横6㎝の長方形があります。
縦3㎝と横8㎝の長方形も面積が24㎠になります。
縦と横の長さが反対のものもあります。
反対ってどういうことですか。
(図形を回転する動作をしながら)縦6㎝と横4㎝、縦8㎝と横3㎝の長方形です。
横の長さが変わっていくと、それに伴って何が変わっていますか。
長方形の形が変わります。
縦の長さが変わっていくからね。

xとyが整数値の組み合わせをすべて整理したら、「xとyが小数だったらほかにもある」という考え方に広げていきます。小数値を扱うことで、グラフの学習をするとき、反比例のグラフは直線ではなく、なめらかな曲線になることを理解させる際に活用しましょう。
(xとyが整数値になるすべての24㎠の長方形が出たら)では、面積が24㎠になる長方形は、この8種類で全部ですね。
小数も入れるともっとできます。
例えば、x、yがどんな小数だったらできますか。(ロイロ)ノートに書きだしましょう。
縦2.4㎝と横10㎝の長方形もあります。
縦1.2㎝と横20㎝の長方形もあります。
縦5㎝と横4.8㎝も面積24㎠になります。
小数だと、いくらでもできそうです。
1人1台端末活用ポイント1
導入や見通しの場面
ロイロノートのテキスト機能を使用し、個人で面積が24㎠になる長方形をかかせます。思い浮かんだ長方形を短時間でメモのようにたくさんかき込んだり、さっと消したりできるので、導入や見通しの場面でタブレットを活用するときに有用です。子供たちの考えは提出箱に提出させ、全体でも共有します。
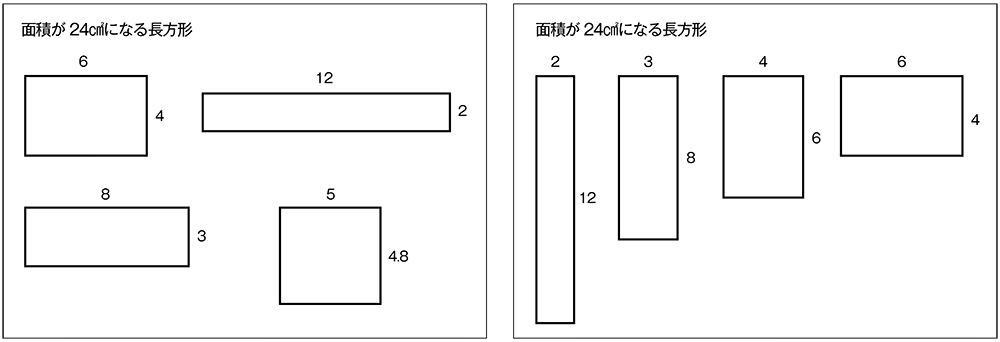
見通し②
では、二つの長さの関係は、どのように調べるとよいでしょうか。
表に表せば、二つの量の関係を調べられると思います。
そうだね。比例の関係を調べるときに表を使ったね。
自力解決の様子
A つまずいている子
二つの量の関係を、表からどのように見付ければよいか分からない。
B 素朴に解いている子
比例のきまりを学習したときのことを想起しながら、表を横に見て、二つの量の変わり方の特徴を考えている。
C ねらい通り解いている子
比例の場合と比較しながら、表を横や縦に見て、二つの量の変わり方の特徴を見付け、矢印や式、言葉でノートにまとめている。
学び合いの計画
Aは、横の長さx㎝と縦の長さy㎝の二つの量を表にまとめることはできても、表のどの部分をどのように見ると変化のきまりや対応のきまりを見付けられるのかが分かっていません。つまり、表から何を見ればよいかが分かっていません。二つの量の関係ではなく、一つの量の変化だけを捉えています。二つの量の関係性を捉えることがまだ難しいのかもしれません。
イラスト/横井智美

