小6算数「分数のわり算」指導アイデア
執筆／埼玉県公立小学校教諭・森田麻実
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
（本時2／7時）
ねらい
真分数÷真分数の計算の仕方を図や式を用いて考え、説明することができる。
評価規準
わり算に関して成り立つ性質を用いて、分数÷分数の計算の仕方を説明することができる。
問題場面
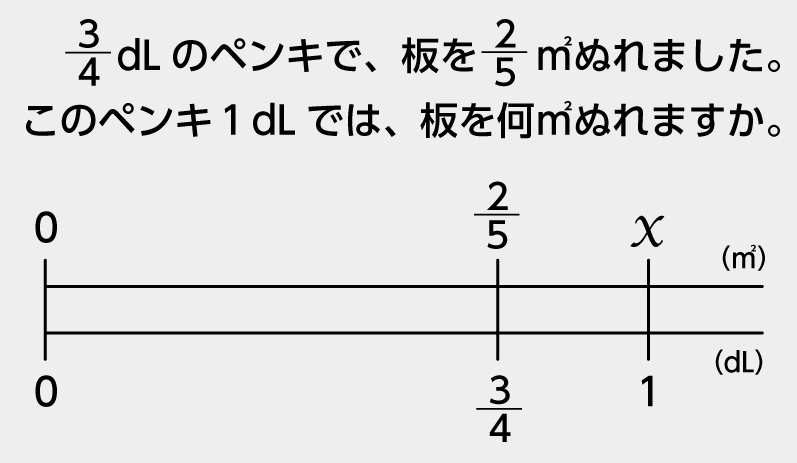
前時では、1dLでぬれる面積を求めるときには、使った量が分数でも整数や小数と同じように式を立てることができました。[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]と立式したわけを説明してください。
ペンキの量が2dLの場合だと、[MATH]\(\frac{2}{5}\)[/MATH]÷2だから、ペンキの量が分数になってもぬった面積÷使った量なので[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]となりました。
数直線に表して、1dLでぬれる面積xを求める式なので、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]となりました。
今日は[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]の計算の仕方を考えていきましょう。
本時の学習課題
分数でわる計算のしかたを考えよう。
見通し
わる数が分数だから、このままでは計算ができない。わり算の性質を使ってわる数を整数にできないかな。
[MATH]\(\frac{1}{4}\)[/MATH]dLをもとにして考えてみよう。
[MATH]\(\frac{3}{4}\)[/MATH]dLを何倍かして整数にして計算してみよう。
わる数を1にして計算してみよう。
自力解決の様子
学び合いの計画
分数を小数に直して計算しても、商が割り切れない場合があることに気付かせた後、わり算の性質を用いれば、除数が整数にすることができることを理解するようにします。
イラスト／横井智美
『教育技術 小五小六』2021年6/7月号より
