小4算数「１けたでわるわり算」指導アイデア《あまりのない２位数÷１位数の計算のしかた》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2022.03.15

単元の展開

第１時　あまりのない、なん十やなん百のわり算（60÷3、600÷3）や、各位とも割り切れるあまりのない２位数÷１位数（63÷3など）の計算のしかたを説明する。
▼　　　　
第２時（本時）あまりのない２位数÷１位数（72÷3など）の計算のしかたを、既習の計算を基にして説明する。
▼
第３時　あまりのない２位数÷１位数（72÷3など）の筆算のしかたを理解する。
▼
第４時　各位とも割り切れずあまりのある２位数÷１位数（93÷4など）の筆算のしかたを説明する。
▼
第５時　十の位が割り切れるあまりのある２位数÷１位数（83÷4など）の筆算のしかたを説明する。
▼
第６時　各位とも割り切れない３位数÷１位数＝３位数（472÷3など）の筆算のしかたを、既習のわり算の計算のしかたを基に説明する。
▼
第７時　商に空位を含み割り切れる３位数÷１位数＝３位数（642÷6など）の筆算のしかたを説明する。
▼
第８時　首位に商が立たない３位数÷１位数（252÷6など）の筆算のしかたを説明する。
▼
第９時　２位数÷１位数＝２位数の暗算と商がなん十、なん百なん十になる３位数÷１位数の暗算のしかたを考える。
▼
第10時　他国のわり算の筆算のしかたを知り、自国のわり算の筆算のしかたと比べ、共通点や相違点を見出す。
▼
第11時　問題に取り組み、学習内容の定着を確認し、理解を確実にする。

本時のねらい（割り切れる2位数÷1位数［63÷3］の後／筆算形式の学習は次時）

あまりのない２位数÷１位数の計算する方法を、これまでに学習したわり算の意味や計算のしかたを基に考える。

評価規準

あまりのない２位数÷１位数の計算の方法を、位ごとに分けて考え、その手順を言葉や図を用いながら説明している。（思考･判断･表現）

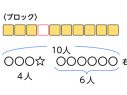
72まいの色紙を３人で同じ数ずつ分けます。１人分はなんまいになりますか。

式は72÷3になるね。

答えは、どれくらいになりそうですか。

20×3＝60だから、72枚を3人で分ければ、20枚よりは多いです。

30×3＝90だから、30枚は無理です。答えは、30枚よりは少なそうです。

では、どのように考えるとできそうですか。

前の時間のように、割られる数を分けて考えるとできそうです。

72をどのように分けますか。

72を前の時間のときのように、十の位と一の位に分けて、70と2に分けて考えるとできそうです。

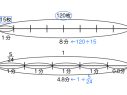
でも、それだと70÷3は計算しにくいし、2÷3は計算できないから、違う分け方で考えたほうがよいと思う。例えば、60と12に分けて考えると、計算しやすいよ。

どうして、60と12に分けようと思ったのですか。

割る数が3だから、60と12に分ければ、60÷3も12÷3もあまりがないから計算しやすいと考えました。

そうか。60と12に分けて考えると、60÷3＝20、12÷3＝4で合わせて24になるから、あまりを考えなくてよいので計算しやすいね。

でも、割る数を見て、あまりがないように割られる数を分けるのは、少し難しいな。

位ごとに分けて考えられると楽なのだけれど……。

割られる数を位ごとに分けて計算する方法を考えよう。

見通し

60÷3＝20、12÷3＝4だから、答えは24になりそうだ。（結果の見通し）

72÷3の割られる数を70と2に分けて70÷3から計算していき、あまりをうまく処理すればできそうだ。（方法の見通し）

自力解決の様子

A つまずいている子

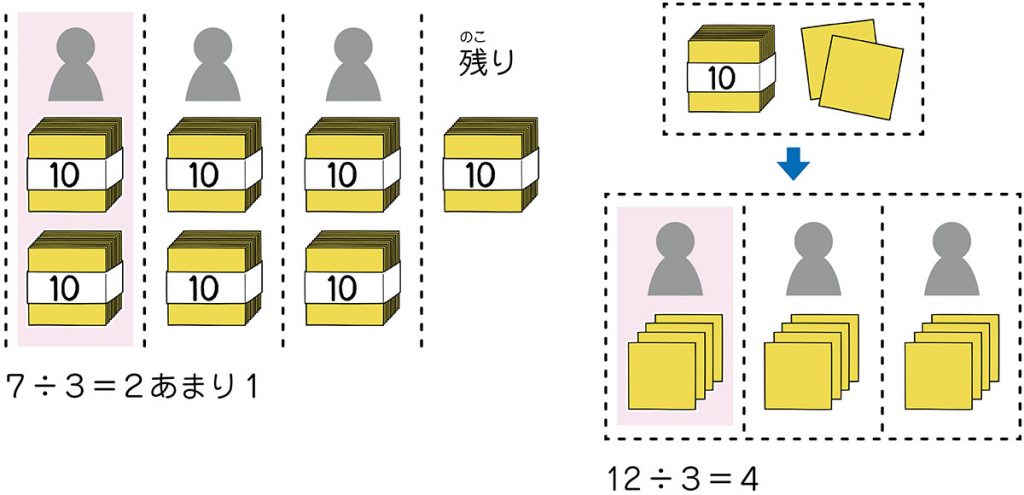
十のまとまり（十の位）の７÷３＝２あまり１の、あまりの処理のしかたに困っている。

Ｂ素朴に解いている子

60÷３＝20
12÷３＝４
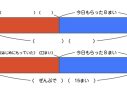
図を使って72を３つに分けて、24枚を求めているが、考えの流れを説明することまではできない。
※かけ算（20×３＝60、４×３＝12）を拠りどころにして考えている。

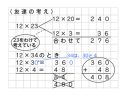
Ｃねらい通り解いている子

72 ÷ 3 ＝ 24
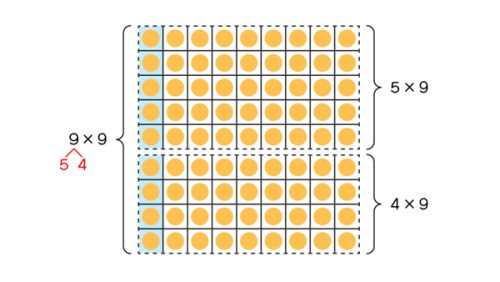
はじめに、10のまとまり（十の位の数）を３人で分ける。そうすると、式は７÷３で、答えは２（20）あまり１（10）となる。次に、残りの１（10）との２を合わせて12枚とし、その12枚を３人で分ける。そうすると、12÷３＝４となる。答えは24枚になる。
※図と式を関連付けながら、位ごとに計算する方法を説明している。