小6算数「速さ」指導アイデア《単位時間あたりの距離で速さを比較する》
国立教育政策研究所教育課程調査官の監修による、教科指導のアイディアと授業のヒントをまとめた指導計画例です。特にポイントとなる時間に焦点を絞って解説しています。
執筆/埼玉県公立小学校教諭・清原一樹
編集委員/国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準(本時の位置 2 / 11 単元の導入)
【ねらい】
距離も時間も異なる場合の速さの比べ方を工夫して考える。
【評価規準】
速さの比べ方を単位量当たりの大きさの考えを基にして考えることができる。(数学的な考え方)
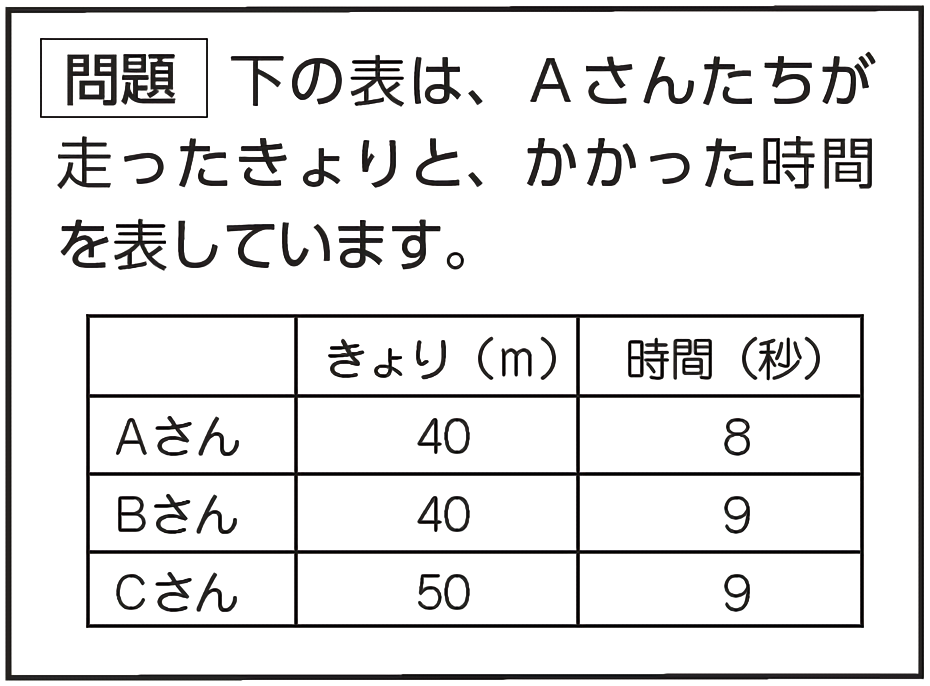
AさんとBさん、BさんとCさんはすぐ比べられたのは、なぜでしたか?
AさんとBさんは距離が同じなので、時間で比べれば、Aさんが速いことが分かります。
BさんとCさんは時間が同じなので、距離で比べれば、Cさんが速いことが分かります。
そうでしたね。今日はAさんとCさんを比べたいのですが、すぐに分かるかな?
距離も時間も異なるから、このままでは比べられないな。
本時の学習のねらい「きょりも時間もことなる場合の速さの比べ方を考えよう。」
【見通し】
第1時では、AさんとBさん、BさんとCさんの速さ比べを行いました。その際、課題を教師から投げかけるのではなく、「距離が同じであること」「時間が同じであること」に気付かせ、どこに着目すれば比較ができるかについて考えさせます。「距離が同じ」であるなら、かかる時間が短い方が速く、「時間が同じ」であるなら、距離が長い方が速いことが分かります。
ここで大切なのは、「距離か時間のどちらかの数値が揃っていれば、速さは比べることができる」ということです。このアイディアを強調することで、本時の課題である「距離も時間も異なる場合」においても、距離か時間を揃えることで求めることができるのではないかという、子供の発想につながっていくはずです。
【自力解決の様子】
A つまずいている子
そのままの数値で、感覚的に比べようとしている。
距離は10 m差があって、時間は1 秒違うから……。
B 素朴に解いている子
「揃える」というアイディアを生かし、公倍数を用いる。
40 と50 の公倍数は200 なので、200 mにかかる時間は……。
C ねらい通りに解いている子
単位量あたりの考えを使っている。
1 秒間当たりに何m進んだかで比べよう。1m当たりに何秒かかったかで比べよう。
【学び合いの計画】
ここでは、3 人組になって自分の考えを紹介する活動を行います。見通しで「距離か時間のどちらかを揃えれば比べることができる」ということを確認しているので、子供は「どのような揃え方があるか」について関心があることが予想されます。そこで3 人組で交流することで、自分の考えと異なる揃え方があれば参考になるはずです。同じアイディアであっても、自分の考えに自信が持てます。この後の全体での練り上げの際、全員が「揃えればできる」という、同じ土俵の上で話が進められるようにすることが大切です。
【ノート例】
【全体発表とそれぞれの考えの関連付け】
練り上げの場面では、「揃える」というアイディアを、どのように扱ったのかを紹介していきます。その際、最初に公倍数の考えを扱うことで、自力解決が難しかった子供にも、感覚的に「揃える」ことを実感させることができます。その
後、五年生で扱った「単位量当たりの考え」を紹介することで、1当たりに揃えると計算で求められることに気付かせたいものです。そして、それぞれの考えを比較していくことで、1当たりに揃えていくと、計算で求めることができるよさの他にも、複数を同時に比べることができるよさや、一目で比べられるよさを子供に実感させていきます
【まとめ】
『距離か時間をそろえれば比べられる。1当たりで比べると、どんな時でも比べられる。』
まとめでは、単位量当たりの考えが便利であることをおさえます。「1当たり」で比べることで、パッと見て判断ができるよさに気付かせたいものです。また「1m当たりにかかる時間」か「1秒当たりに進む距離」のどちらが分かりやすいかにも触れ、「1秒当たりに進む距離」は、数値が大きくなるほど速くなることを表すので、この方が比べやすいことに気付かせ、これが「速さ」を表していることにつなげていきます。
評価問題
Aの店ではすしが5分間に35 m進み、Bの店では2分間に16 m進みます。すしが進む速さは、どちらの店が速いですか。
子供に期待する解答の具体例
1分間当たりに進む距離で比べる。
Aの店……35 ÷5=7
Bの店……16 ÷2=8 Bの店の方が速い
本時で扱ったように、速さを比べる方法は何通りかあります。その中で、比べるために効率的である「1単位時間で進む距離」を使って答えを出させます。ここでは1単位時間が「分」になっていますが、「秒」と同様に計算で求められることを確認します。
本時のねらいと評価規準(本時の位置 9/ 11 速さの意味の拡張)
【ねらい】
作業の速さも単位量当たりの大きさの考えを用いて、比べられることを理解する。
【評価規準】
単位量当たりの大きさの考えを用いて、作業の速さなどの比べ方を考え、説明している。(数学的な考え方)
『問題』
A、B2つのプリンターがあります。Aのプリンターは1時間で90枚、Bのプリンターは12 分で20枚印刷することができます。速く印刷できるのは、どちらのプリンターですか。
今までの問題とは、何が違うでしょうか。
速さを聞かれているけど、道のりは出てこないよ。
道のりの代わりに枚数が出てくるね。
印刷も速さで表すことができるね。
プリンターの印刷の速さは、どうやって比べたらいいかな。今までに学習した考え方がうまく使えないかな。
本時の学習のねらい「作業をする速さについて考えよう。」
イラスト/横井智美
『小六教育技術』2018年7/8月号より


