小３算数「分数」指導アイデア《0.1を単位とした小数と十分の一を単位にした分数の大きさの関係》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.12.26

年間指導計画

年間指導計画はこちらをクリック

・かけ算
・時刻と時間
・わり算
・たし算とひき算の筆算
・棒グラフと表
・余りのあるわり算
・長さ
・暗算
・かけ算の筆算　１けた
・１万を超える数
・円と球
・重さ
・わり算や分数
・何倍でしょう
・小数
・分数
・三角形と角
・計算の順序
・式と計算
・かけ算の筆算　２けた
・そろばん

単元の展開（各時の主な学習活動内容）

第１時　１ｍを等分してできる大きさの分数による表し方
第２時　単位分数を用いた分数の表し方
第３時　分数・分母・分子の意味、端数部分の大きさの分数による表し方
第４時　分数を数直線上に並べ、分数を整数と同様の数として捉える。
第５時　１より大きい分数の表し方
第６時　分割分数と量分数の違いについて理解
第７時（本時）0.1を単位とした小数と[MATH]\(\frac{1}{10}\)[/MATH]を単位にした分数の大きさの関係
第８時　同分母の分数の加法・減法の計算

本時のねらい

分母が10の分数と[MATH]\(\frac{1}{10}\)[/MATH]の位までの小数の関係について理解する。

評価規準

[MATH]\(\frac{1}{10}\)[/MATH]の表す意味や0.1の表す意味に着目して、分数で表せる大きさと小数の関係を考え、説明している。

本時の教材のポイント

ここでは、１を10等分したときの数の表し方を基に、分母が10の分数と小数の大きさについて考えていきます。分数を数として捉えることができるようにするために、「１を何等分した大きさであるか」と単位分数を捉えられるように確認したり、小数とともに数直線上に示した分数の位置を確認したりすることで、分数も数であることを視覚的に理解できるようにしていきます。

はじめに１を10等分した目盛りの入っている数直線を配付し、目盛りに合うように数を書くよう指示をします。そのときに、今まで学習していた分数を書く場合もあれば、小数を書く場合もあります。一人一人の数直線に数を書き込むことができたら、今日の問題である数の大きさ比べをすることを知らせます。その後、教師が「どんな数を書きましたか？」と問い、分数と小数の２つの表し方を子供から取り上げます（もし全員が分数で表した場合は、教師から小数の数直線を提示します）。

次に、本時の問題である[MATH]\(\frac{4}{10}\)[/MATH]（分数）と0.6（小数）を比べることを示し、数直線を使って解いていくことを確認します。そのとき、自分とは違う数の表し方をした友達の数直線を見ながら、目盛りに書いた数は違っても、１目盛りの大きさが同じだということに、協働的な活動を通して気付けるようにしていきます。ここで、１目盛りの大きさが等しいことから、[MATH]\(\frac{1}{10}\)[/MATH]と0.1は大きさが等しいと言ってよいのかという問題意識が生まれるようにすることで、本時の課題へとつなげていきます。

「１目盛りに、[MATH]\(\frac{1}{10}\)[/MATH]（0.1）と目盛りを書いたのはどうしてですか？」と、目盛りの表し方を教師が問うことで、１目盛りの大きさを分数で表しても小数で表しても、どちらも１を10等分していることが同じであることから、[MATH]\(\frac{1}{10}\)[/MATH]と0.1は大きさが等しいことを押さえます。

数の大小を表すときには不等号を使ったことにも触れながら、不等号を使って[MATH]\(\frac{4}{10}\)[/MATH]と0.6の大きさを表します。数の大きさを比べるときに、教師は「[MATH]\(\frac{4}{10}\)[/MATH]は、[MATH]\(\frac{1}{10}\)[/MATH]の何個分ですか」や、「0.6は0.1の何個分ですか」と、[MATH]\(\frac{1}{10}\)[/MATH]や0.1の表す意味を確認しながら、分数と小数の大きさについて確認していくことで、分数と小数の大きさを捉えられていない子供も理解できるようにしていきます。ここで、改めて単位分数を意識して説明したり、数直線の位置を確認したりすることを繰り返すことで、分数を数として捉えることにつながっていきます。

本時の展開

昨日の分数の学習で出てきた[MATH]\(\frac{3}{4}\)[/MATH]ｍと、２ｍの[MATH]\(\frac{3}{4}\)[/MATH]には、どのような違いがありましたか。

[MATH]\(\frac{3}{4}\)[/MATH]ｍはもとの長さが１ｍのときで、２ｍの[MATH]\(\frac{3}{4}\)[/MATH]は、もとの長さが２ｍなので、もとの長さが違いました。

[MATH]\(\frac{3}{4}\)[/MATH]だから同じかと思ったけれど、違う長さだったね。

分数は、もとの長さに注目することが大切でした。

今日の問題です。目盛りに数を書いてみましょう。（分数を書く子供と小数を書く子供がいることが予想される）

※１を10等分している数直線を配付する。

これから、数の大きさ比べをします。

分数を比べるのかな。

私は小数を書いたよ。

[MATH]\(\frac{4}{10}\)[/MATH]と0.6では、どちらが大きいですか。

分数と小数だ。

どうやって比べるのかな。

この数直線だとどこかな。

１目盛りの大きさはいくつになりましたか。

１までの目盛りが10等分されているから、１目盛りは[MATH]\(\frac{1}{10}\)[/MATH]と考えました。

１までの目盛りが10等分されていることは同じで、10等分されているから、１目盛りは0.1だと考えました。

分数で考えた子と、小数で考えた子がいるから、一緒に見たら比べられそう。

２つの数直線を見てみましょう。

※小数の目盛りが入っている数直線と、分数が入っている数直線を提示する。

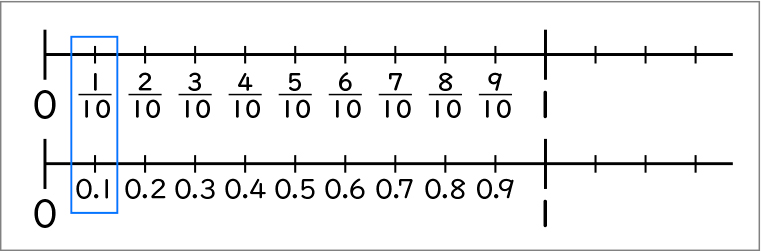
目盛りでは、0.1と[MATH]\(\frac{1}{10}\)[/MATH]は同じ位置にあります。

同じ大きさなのかな。

分母が10の分数と小数の大きさについて考えよう。

数直線だと同じ位置にありますね。本当に同じ大きさなのかを考えてみましょう。
（どちらも１を10等分したうちの１つ分であることを板書に残していく）
分数で表した場合は、１を10等分したうちの１目盛りが[MATH]\(\frac{1}{10}\)[/MATH]です。小数で表した場合は、１を10等分したうちの１目盛りが0.1です。

どちらも、１を10等分しているところが同じです。

そうですね。どちらも１を10等分していることが同じなので、[MATH]\(\frac{1}{10}\)[/MATH]と0.1は等しい大きさの数です。（[MATH]\(\frac{1}{10}\)[/MATH]＝0.1の板書をする）
みなさんの数直線の目盛りに小数と分数を書いてみましょう。そして、[MATH]\(\frac{4}{10}\)[/MATH]と0.6では、どちらが大きいのかを考えましょう。

見通し

[MATH]\(\frac{1}{10}\)[/MATH]の下は0.1（0.1の下は[MATH]\(\frac{1}{10}\)[/MATH]）だから、書いてみよう。

0.1の下は[MATH]\(\frac{1}{10}\)[/MATH]（[MATH]\(\frac{1}{10}\)[/MATH]の下は0.1）だから、順番に書いていこう。

[MATH]\(\frac{1}{10}\)[/MATH]の下は0.1（0.1の下は[MATH]\(\frac{1}{10}\)[/MATH]）だから、順番に書いていこう。数の大きさは不等号を使って表そう。

自力解決の様子

Ａ　つまずいている子

・[MATH]\(\frac{1}{10}\)[/MATH]の下に0.1（0.1の下に[MATH]\(\frac{1}{10}\)[/MATH]）と書くが、そのあとが書けないで止まってしまう。

Ｂ　素朴に解いている子

・[MATH]\(\frac{1}{10}\)[/MATH]の下に0.1（0.1の下に[MATH]\(\frac{1}{10}\)[/MATH]）と書き、その後は順番に数を書いていく。

・[MATH]\(\frac{4}{10}\)[/MATH]と0.6は、0.6のほうが大きいとノートに書いている。

Ｃ　ねらい通り解いている子

・[MATH]\(\frac{1}{10}\)[/MATH]の下に0.1（0.1の下に[MATH]\(\frac{1}{10}\)[/MATH]）と書き、その後は順番に数を書いていく。

・[MATH]\(\frac{4}{10}\)[/MATH]と0.6は、0.6のほうが大きいことを不等号を使って表している。

・[MATH]\(\frac{4}{10}\)[/MATH]＝0.4もしくは、0.6＝[MATH]\(\frac{6}{10}\)[/MATH]など、小数から分数へ表し方を変えた記述をしている。

ノート例

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

数の大小は不等号を使って書けるね。

これで、どっちが大きいか比べられる。

[MATH]\(\frac{4}{10}\)[/MATH]は0.4だから、0.6と比べると、0.6のほうが大きい。

数直線を見て確認してみましょう。0.4は0.1の何個分ですか。

0.4は0.1の４個分です。

分数でも同じように考えられるよ。

[MATH]\(\frac{4}{10}\)[/MATH]は[MATH]\(\frac{1}{10}\)[/MATH]の何個分ですか。

[MATH]\(\frac{4}{10}\)[/MATH]は[MATH]\(\frac{1}{10}\)[/MATH]の４個分です。

どちらも、４個分が同じです。

数直線で見ても４個分の大きさが同じですね。では、0.6と大きさの等しい分数は何ですか。

[MATH]\(\frac{6}{10}\)[/MATH]です。

大きさの等しい数を表す方法は、小数と分数の２つがあるね。

学習のまとめ

１を10等分すると、分数と小数の２つの表し方がある。
[MATH]\(\frac{1}{10}\)[/MATH]＝0.1

小数第一位のことを、[MATH]\(\frac{1}{10}\)[/MATH]の位とも言う。

評価問題

□にあてはまる等号やふ等号を書きましょう。

① [MATH]\(\frac{8}{10}\)[/MATH]□0.9

② [MATH]\(\frac{3}{10}\)[/MATH]□0.3

③ [MATH]\(\frac{1}{10}\)[/MATH]□０

子供に期待する解答の具体例

①[MATH]\(\frac{8}{10}\)[/MATH]は0.8だから…　＜
　0.9は[MATH]\(\frac{9}{10}\)[/MATH]だから…　＜

②[MATH]\(\frac{3}{10}\)[/MATH]は0.3だから…　＝
　0.3は[MATH]\(\frac{3}{10}\)[/MATH]だから…　＝

③１は[MATH]\(\frac{10}{10}\)[/MATH]だけれど、０より小さい数はないから…　＞

感想例

大きさの等しい数を表す方法は分数と小数の２つあることが分かりました。
分数と小数でも数の大きさが比べられることが分かりました。１を10等分した分数でない場合も比べられるのか気になりました。
[MATH]\(\frac{1}{10}\)[/MATH]と０を比べたときに、[MATH]\(\frac{1}{10}\)[/MATH]のほうが小さい気がしたけれど、数直線を見て考えたら、[MATH]\(\frac{1}{10}\)[/MATH]は０よりも大きいことが分かりました。