小2算数「1000より⼤きい数」指導アイデア《数のまとまりに着目して、数の相対的な大きさを捉える》

執筆/新潟⼤学附属新潟⼩学校教諭・⽯塚正⼈
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、新潟県新潟市立上所小学校教諭・志田倫明
目次
年間指導計画
・表とグラフ
・時刻と時間
・2けたのたし算
・2けたのひき算
・長さ
・1000までの数
・水のかさ
・大きい数のたし算とひき算
・三角形と四角形
・式と計算
・かけ算(1)
・かけ算(2)
・かけ算(3)
・1000より大きい数
・たし算とひき算の関係
・図を使って考えよう
・分けた大きさ
・箱の形
単元の展開(各時の主な学習活動内容)
第1時 4位数の読み方や表し方について考える。
第2時 空位のある4位数の表し方について考えるとともに、数の仕組みに着目して、4位数を書いたり読んだりする。
第3時 位取り板と数カードを使って各位の数を読み取ったり、4位数を数カードで表したりする。
第4時 4位数の構成を、等式を使って表す。
第5時(本時)数のまとまりに着目して、数の相対的な大きさを捉える。
第6時 数直線の1目盛りの大きさや、指示された目盛りの数を読んだり、数直線上に表したりする。
第7・8時 10000の構成、数の読み方、書き方及び10000付近の数について考える。
第9時 10000までの数の構成を多面的に捉え、数の見方を豊かにする。
第10時 身の回りから数が使われている場面を探し、数には、ものの大きさを表しているものと、表していないものがあることを知る。
第11時 学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。
本時のねらい
数のまとまりに着目して、数の相対的な大きさについて理解する。
評価規準
10や100、1000のまとまりを用いて、4位数の構成を考えたり、大小比較したりすることができる。
本時の教材のポイント
本時では、数をある位の単位(例えば、十、百、千、あるいは0.1、0.01など)に注目して、それが「いくつ分」あるかという見方である数の相対的な大きさについて理解するために、「大きいほうを選びましょう」という二者択一のゲーム場面を提示します。
まず、100円や500円、1000円札など硬貨や紙幣のイラストを提示します。子供は、提示されたものを見て数を構成し、どちらのほうが大きいか判断します。次に丸の中に数字をかいたものや数字カードを提示します。このように、提示するものの抽象度を段階的に上げることが、つまずいている子供にとっても、ヒントになるでしょう。
また、提示するだけでなく、子供の1人1台端末に配信することで、数字カードを動かしてまとめたり、そこに書き込んだりしながら考えることができるようになります。さらに、これまでに学習した位取り表をいつでも使えるようにしておくとよいでしょう。つまずいている子供への支援としてだけでなく、数の構成についての理解を深めることができます。
本時の教材のポイントとしては、デジタルとアナログとの融合があげられます。1人1台端末に配信した問題に書き込むのもよし、数字カードをおはじきなどの半具体物に置き換えて操作するもよし、その子なりのやりやすさに応じて、デジタルかアナログかを選べるとよいでしょう。また、その操作の過程を共有することで、協働的な学びを促すことが期待できます。
本時の展開
今日は「大きいほうを選びましょう」というゲームをします。
なんだか面白そう。
第1問です。どちらが大きいですか。
※2、3秒で画面を切り替える。
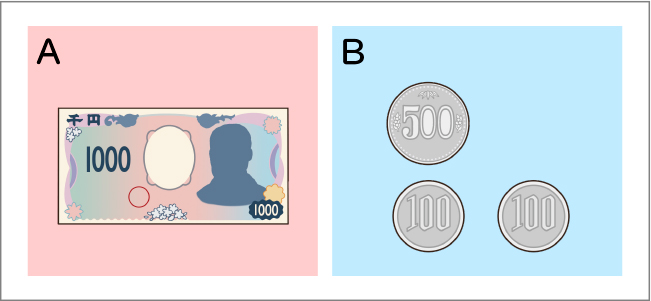
簡単だよ。Aのほうが大きいよ。
どうしてですか。
だって、Aは1000円で、Bは700円だからです。
Bは500円が1枚と100円が2枚で合わせて700円になります。
第2問です。どちらが大きいですか。
※2、3秒で画面を切り替える。
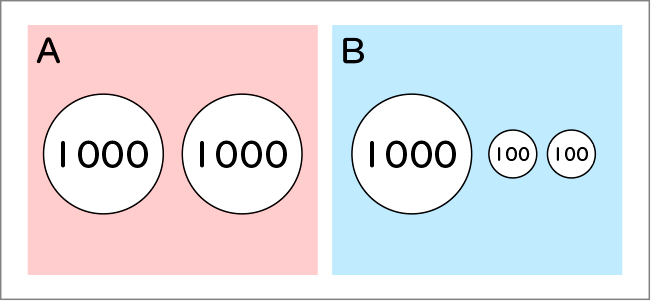
これもAです。
Aは1000が2つで2000、Bは1000が1つと100が2つで1200です。
第3問です。どちらが大きいですか。
※2、3秒で画面を切り替える。
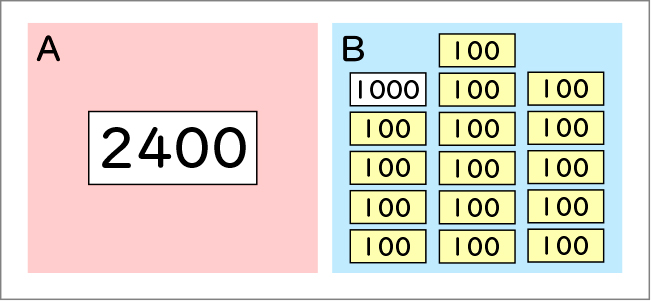
困ったな。これは難しくて、よく分からないです。
難しいのはどこですか。
Bには100がいっぱいあったけれど、いくつかよく分からないからです。
だから、どちらが大きいか比べられませんでした。
では今日は、AとBをどうやって比べたらよいか考えてみましょう。

AとBを⽐べるには、どうしたらよいだろうか。
見通し
- Bがいくつか分からないから、まずは100のカードが何枚あるか数えてみよう。
- Bがいくつか分からないから、1000から100ずつ数えてみよう。
自力解決の様子
A つまずいている子
・Bの100のカードが何枚あるのか数えるが、数の構成が分からずどちらが⼤きいか分からない。
B 素朴に解いている子
・Bの1000のカードをスタートとし、1100、1200、1300……と数えていくことでBが⼤きいことが分かる。
C ねらい通り解いている子
・Bの100のカードが10枚で1000になることが分かる。
・100のカードが15枚あることから1500となり、1000のカードと合わせて2500になることから、Bが⼤きいことが分かる。
全体発表とそれぞれの考えの関連付け
まず、どちらのほうが大きいか、全員で確認しましょう。
Bが大きいです。
では、どうやって比べたのか発表してください。
私は、Bに1000のカードがあったので、1000から100ずつ数えていきました。1100、1200、1300……と数えていくと、Bは2500になりました。
私は、Bの100のカードが何枚あるのかを調べました。数えると、15枚ありました。100が15個あるということなので、1500になります。1000と1500なので、合わせて2500になります。
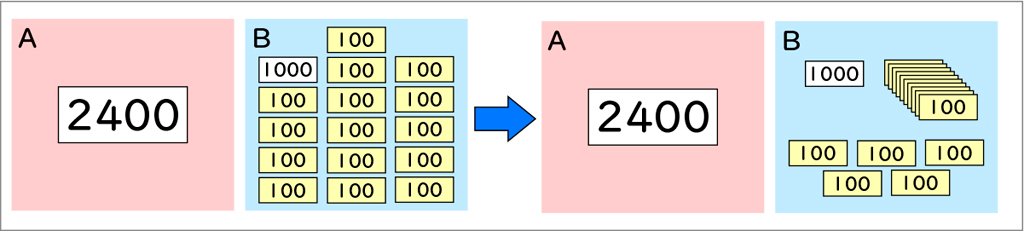
これまでに学習したものを使って、説明できますか。
位取り表にまとめて説明します。
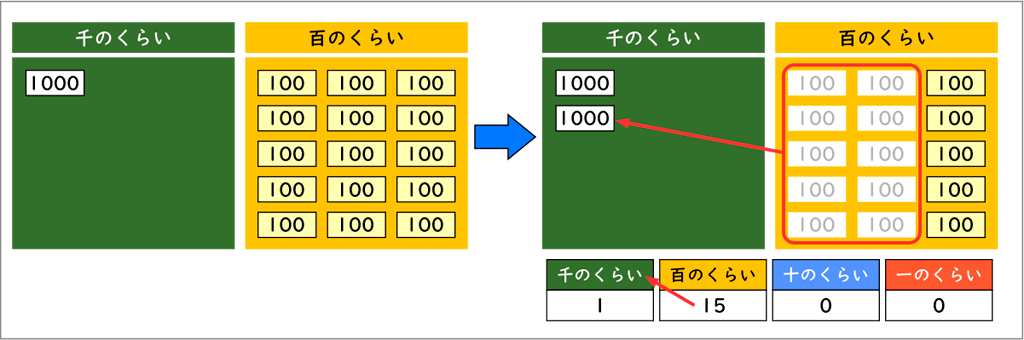
100が10個で1000になるので、100のカードが10枚で1000のカード1枚になります。こうすると、1000のカードが2枚、100のカードが5枚になるので、2500になります。
これまでのように、100や1000のまとまりがいくつあるのかを考えると、比べることができます。
まとめ
構成/桧貝卓哉 イラスト/横井智美・やひろきよみ 図版作成/永井俊彦

