小６算数「拡大図・縮図」指導アイデア《１つの頂点を中心とした拡大図・縮図のかき方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.11.29

単元の展開

第１時　対応する辺の長さを簡単な比で表すことで、拡大図と縮図の意味と性質を理解する。
▼　　　《拡大図と縮図の意味と性質》
第２時　拡大図と縮図について、対応する辺の比から、何倍の図であるかを考える。
▼　
第３時　方眼紙を利用した、拡大図と縮図のかき方を考え、実際にかく。
▼
第４時　対応する辺の長さや角の大きさを使った拡大図のかき方を考える。
▼　　　《対応する辺の長さや角の大きさを基にした拡大図のかき方》
第５時　辺の長さや角の大きさを使った縮図のかき方を考える。
▼
第６時（本時）１つの頂点を中心とした拡大図・縮図のかき方を考える。
▼
第７時　任意の点を中心にした拡大図・縮図のかき方を考える。
▼
第８時　縮尺の意味と表し方を理解する。
▼
第９時　身の回りの長さの測定に縮図の考えを活用して、実際の長さを求める。
▼
第10時　学習内容の習熟・定着を図る。

本時のねらい

１つの点を中心とした拡大図・縮図のかき方を考え、その方法を表現する。

評価規準

図形を構成する要素及び図形間の関係に着目し、見いだした拡大図や縮図の性質を基にして、１つの点を中心にした拡大図・縮図のかき方を考え、説明している。（思考・判断・表現）

本時の展開

光一さんは、三角形ＡＢＣを２倍に拡大してかこうとして、下の図のようにかいたのですが、どうやら自信がなさそうです。三角形ＤＢＥが、三角形ＡＢＣの２倍の拡大図になっているか調べましょう。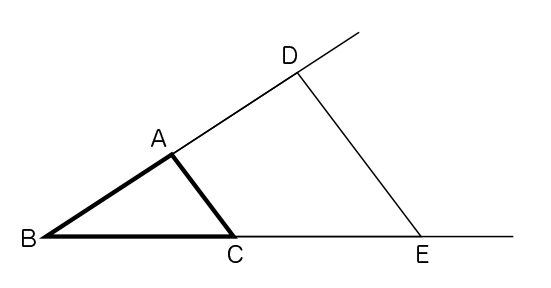

光一さんのかいた三角形ＤＢＥは、三角形ＡＢＣの２倍の拡大図になっていそうですか。

これは、どういう図なの？　昨日は、基の三角形と拡大した三角形が２つ並んでいたけど、光一さんの図は、三角形が１つしかないよ。

三角形ＤＢＥのなかに、三角形ＡＢＣが入っているよ。

三角形ＤＢＥと三角形ＡＢＣが重なっているんだね。

そういうことか。２つの三角形「三角形ＡＢＣと三角形ＤＢＥ」の頂点Ｂが共通しているんだね。

対応している頂点Ｂが共通していて、辺も重なっているということは、２つの三角形の角Ｂの大きさは同じということです。だから、角Ｂをつくっている辺ＢＤと辺ＢＥの長さが、辺ＢＡと辺ＢＣの長さの２倍になっているかどうかを調べたら、２倍の拡大図になっているかどうかが分かると思います。

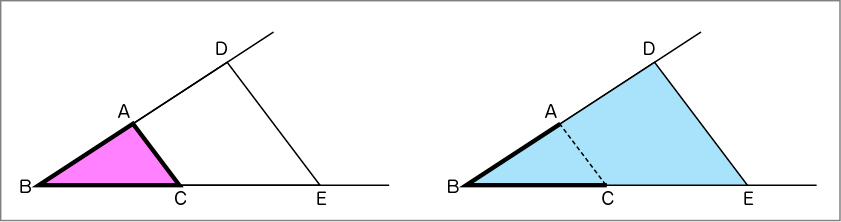
では、対応する辺の長さがそれぞれ２倍になっているのか調べていきましょう。

私は、定規で長さを測って調べました。辺ＢＡ＝４㎝、辺ＢＤ＝８㎝なので、２倍になっていました。辺ＢＣ＝５㎝、辺ＢＥ＝10㎝なので、２倍になっていました。だから、三角形ＤＢＥが、三角形ＡＢＣの２倍の拡大図だと言えます。

僕は、コンパスを使って調べました。辺ＢＤと辺ＢＥの長さが、それぞれ辺ＢＡと辺ＢＣの長さの２倍になっていました。だから、三角形ＤＢＥが、三角形ＡＢＣの２倍の拡大図だと言えます。

１つの点を中心にしても拡大図をかくことができるんだね。

点Ｂを中心にすると、辺ＢＡと辺ＢＣを延長して、定規やコンパスで２倍になる点を見付けるだけで拡大図がかけるから簡単だね。

前の時間に見付けた方法（２つの辺の長さとその間の角の大きさ）を使ったんだね。

三角形の拡大図は、１つの点を中心にして簡単にかくことができることは分かったよ。でも、四角形は１つの点を中心にして拡大図をかくことができるのかな。

やってみよう。

みんなで、四角形の場合について考えていくということでよいですか。

はい、調べてみたいです。（多数）

１つの点を中心にして拡大図をかく方法を使って、四角形ＡＢＣＤの２倍の拡大図四角形ＥＢＦＧをかきましょう。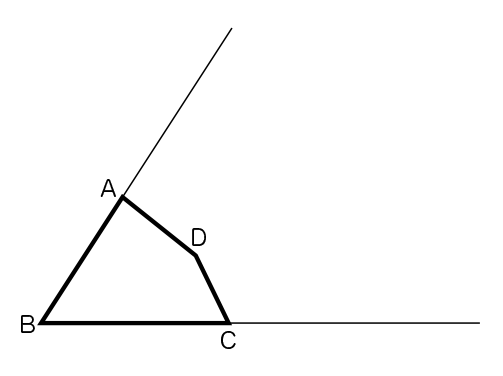

（１人学習中のつぶやき）頂点Ａと頂点Ｃに対応する頂点Ｅと頂点Ｆは見付けることができたけど……。

この後どうしたらいいのかな。頂点Ｅと頂点Ｆを直線で結んだら、三角形になってしまう。

どうしましたか。何か困ったことがありましたか。

はい、困ったことがあります。光一さんのように、１つの点を中心にして作図しようとしたのですが、途中までは同じようにできたけど、続きが分からなくなってしまいました。

私も困っています。１つの点を中心にして作図したら、四角形ではなく三角形ができました。

どういうことなの。

（黒板に作図しながら説明）まず、頂点Ａに対応する頂点Ｅを、光一さんと同じ方法で見付けました。

そうそう。同じようにしました。

次に、頂点Ｃに対応する頂点Ｆを、光一さんと同じ方法で見付けました。

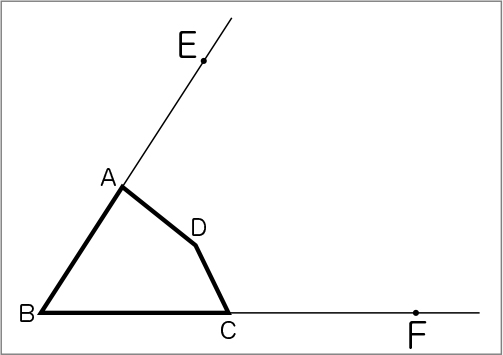
ここまでは同じです。この後、どうしたらいいか分からなくなりました。

私は、三角形の拡大図のとき、対応する２つの頂点を見付けた後、直線で結んだから、今回も同じようにしました。（黒板に作図しながら説明）こんなふうに頂点Ｅと頂点Ｆを結ぶと、三角形ＥＢＦになってしまいました。

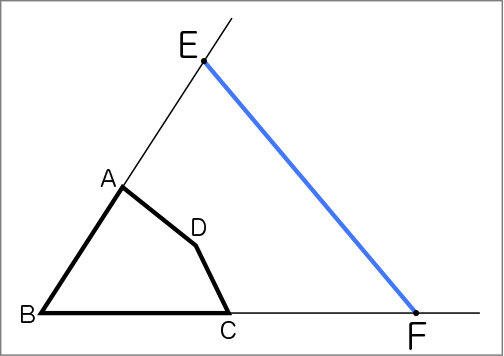
１つの点を中心にして拡大図を作図する方法は、三角形にしか使えないということですか。

いいえ。私は、１つの点を中心にして拡大図を作図する方法は、三角形だけでなく、四角形やその他の多角形にも使えると思います。

でも、四角形の拡大図をかこうとしたら、三角形になってしまったよ。

それは、対応する頂点を３つしか選んでないからだよ。

どういうこと。

四角形ＡＢＣＤの頂点Ａ・Ｂ・Ｃに対応する頂点は見付けているけど、頂点のＤに対応する頂点は見付けていないでしょ。

あっ！　確かに。

でも、どうやって見付けるのかな。だって、頂点Ｅは、辺ＢＡの延長線上にあって、頂点Ｆは、辺ＢＣの延長線上にあったけど、頂点Ｇは、頂点Ｂからの辺の延長線上にはないよ。

確かに。頂点Ｄに対応する頂点Ｇは、どのように見付けたらいいのか考えたらいいね。

頂点Ｄに対応する頂点Ｇの見付け方を考えよう。

見通し

辺ＡＤと辺ＣＤの長さをそれぞれ２倍した長さをコンパスで印をつけてみよう。（方法の見通し）

辺だけではなく、対角線も２倍になるのではないかな。（方法の見通し）

四角形を２つの三角形とみなして考えよう。（結果の見通しなど）

自力解決の様子

A　つまずいている子
・だいたいの２倍の大きさの形をイメージとしてもっている（それぞれの頂点の位置は明確ではない）。
⑴ 辺の長さがだいたい２倍となるところに頂点Ｅと頂点Ｆをとる。
⑵ 四角形ＡＢＣＤの形が崩れないところに頂点Ｇをとり、四角形ＥＢＦＧを作図してみている。

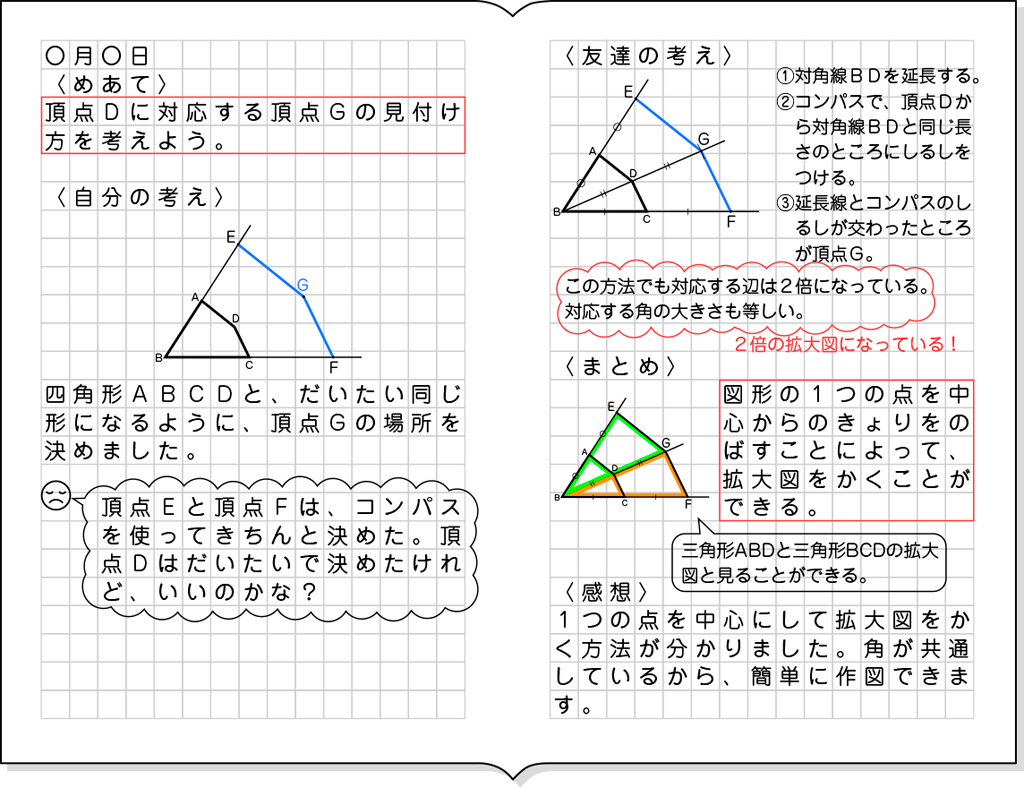
Ｂ　素朴に解いている子
・コンパスを使って、頂点Ｇを見付け出そうとしている。
⑴ 辺ＡＤ＝2.5㎝、辺ＣＤ＝２㎝なので、２倍の拡大図は、辺ＥＧ＝５㎝、辺ＦＧ＝４㎝になります。
⑵ コンパスで、頂点Ｅから５㎝のところに印をつけます。
⑶ コンパスで、頂点Ｆから４㎝のところに印をつけます。
⑷ コンパスの印が交わったところが、頂点Ｇです。

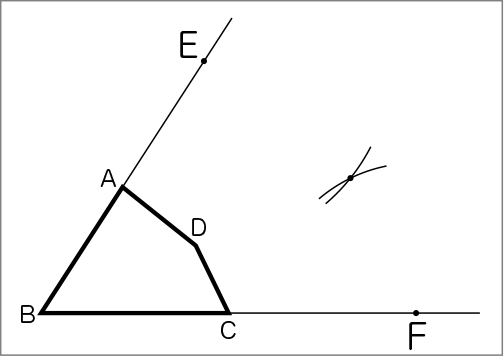
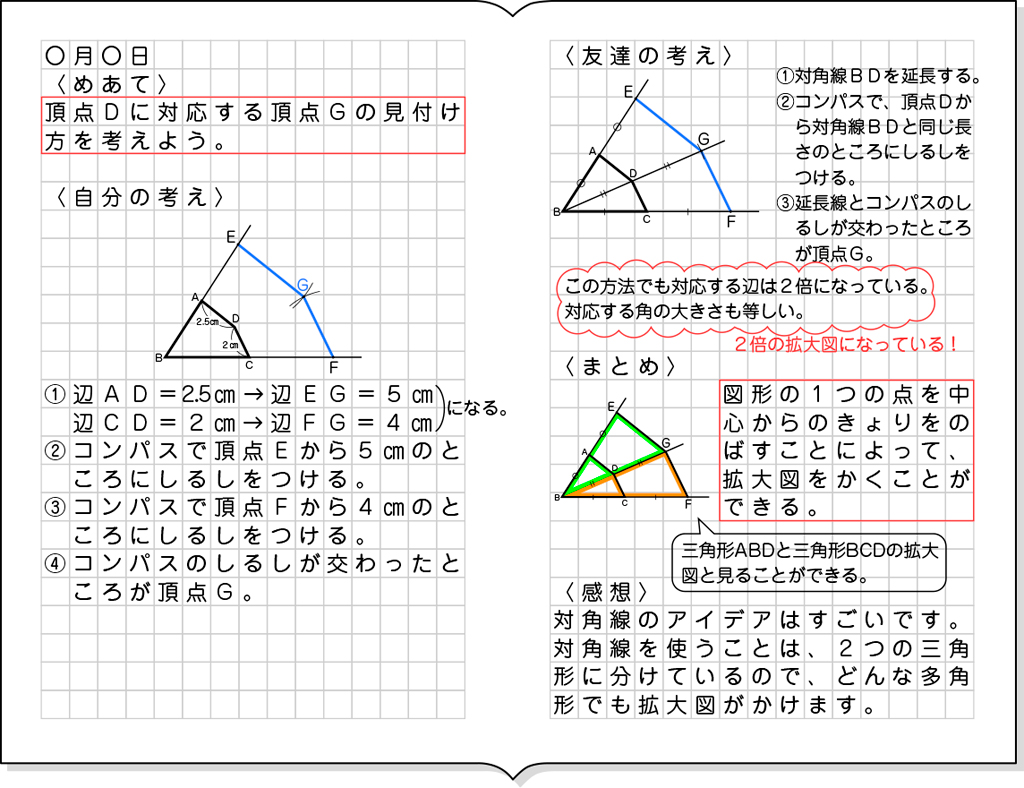
Ｃ　ねらい通り解いている子
・対角線の長さを２倍にして、頂点Ｇを見付け出そうとしている。
２倍の拡大図は、対応する辺の長さが２倍になるだけではなく、対角線も２倍になると考えました。
⑴ 対角線ＢＤを延長します。
⑵ コンパスで、頂点Ｄから対角線ＢＤと同じ長さのところに印をつけます。
⑶ 対角線ＢＤの延長線とコンパスの印が交わったところが、頂点Ｇです。

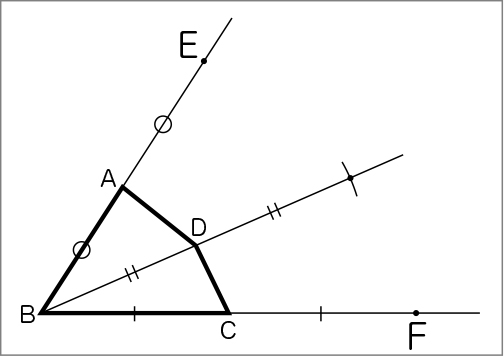
・さらに、作図した四角形ＥＢＦＧが、２倍の拡大図になっているか確かめている。
対応する辺の長さと対応する角の大きさを調べて確かめている。

学び合いの計画

本時は、１つの点を中心にした拡大図の作図の仕方を考える問題場面です。問題場面１では、１つの点を中心にした三角形の拡大図のかき方を学習します。その際、｢本当に２倍の拡大図か考える」｢２倍の拡大図のかき方として正しいかどうか考える」ことで、図形を構成する要素及び図形間の関係に着目しながら、１つの点を中心にした三角形の拡大図のかき方の理解を確かなものにしていくことができます。さらに、子供からの「１つの点を中心にした三角形の拡大図のかき方は分かったけれど、四角形もこの方法で拡大図がかけるのかな」という問いから、問題場面２の場面を設定します。

問題場面２では、頂点Ｇの見付け方が話合いの中心になるでしょう。第４時の学習を生かした考え方（考えＢ）も大事にしながら、対角線の考え方（考えＣ）につなげていきます。その際、対角線の考え方は、２つの三角形に分けて考えれば、問題場面１の方法に当てはまることを確認します。そうすることで、対角線を延長しても拡大図がかけることを説明したり、四角形よりも大きい多角形の拡大図もかけそうだと気付いたりすることができます。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

頂点Ｇを見付けることはできましたか。

（作図したノートをICT機器で大きく提示しながら）四角形ＡＢＣＤの形が崩れないところに頂点Ｇをとりました。だいたいここが頂点Ｇだと思います。

だいたいそこが頂点Ｇだと思うんだけど、だいたいでいいのかな。

だいたいではない頂点Ｇの場所を見付けることができたのですか。

見付けることができました。（黒板に作図しながら説明）辺ＡＤ＝2.5㎝、辺ＣＤ＝２㎝なので、２倍の拡大図は、辺ＥＧ＝５㎝、辺ＦＧ＝４㎝になります。コンパスで、頂点Ｅから５㎝のところに印をつけます。コンパスで、頂点Ｆから４㎝のところに印をつけます。コンパスの印が交わったところが、頂点Ｇです。

私も同じように作図しました。頂点Ｅと頂点Ｆは、頂点Ｂを中心にした問題１と同じ方法で見付けました。でも、頂点Ｇは、その方法は使えないから、前の時間に学習した方法を使いました。

どういうこと？

まず、頂点Ｅと頂点Ｆを見付けたから、三角形ＢＡＣの２倍の拡大図の三角形ＢＥＦの作図ができたことになります。次に、残りの三角形ＤＡＣの拡大図の三角形ＧＥＦを作図します。

なるほど。三角形ＤＡＣと三角形ＧＥＦは重なっていないから、１つの点を中心にした方法ではなくて、対応する辺の長さを２倍する方法で頂点Ｇを見付けたんだね。

この方法を使えば、頂点Ｇの場所をだいたいではなく、正確に見付けられるね。

みなさん、納得できましたか。

はい、分かりました。これで、私も正確な頂点Ｇを見付けることができそうです。

えっ、本当？　どうやったの。

（作図したノートをICT機器で大きく提示する）私が作図した拡大図はこれです。

対角線ＢＤを延長しているよ。どういうこと。

２倍の拡大図は、対応する辺の長さが２倍になるだけではなく、対角線も２倍になると考えました。まず、対角線ＢＤを延長します。次に、コンパスで頂点Ｄから対角線ＢＤと同じ長さのところに印をつけます。対角線ＢＤの延長線とコンパスの印が交わったところが頂点Ｇです。

作図した方法は分かったけど、対角線を２倍にして作図した四角形ＥＢＦＧは、本当に２倍の拡大図になっているのかな。

どうしたら確かめることができますか。

対応する辺の長さや角の大きさを調べてみたらいいと思います。

それでは、確かめてみましょう。

対応する辺は、すべて２倍になっていました。

対応する角の大きさは、それぞれ同じでした。

だから、四角形ＥＢＦＧは２倍の拡大図と言えます。

対角線を２倍にする方法でも拡大図をかくことができることが分かりました。

作図した拡大図を見て思ったのだけど、四角形ＡＢＣＤは、三角形ＡＢＤと三角形ＢＣＤの２つの三角形に分けることができます。この２つの三角形の２倍の拡大図が、三角形ＥＢＧと三角形ＢＦＧになります。

そうか！　対角線を２倍にした方法は、問題１の方法と同じ考え方だね。

四角形は三角形に分けて、それぞれの拡大図をつくることによって、拡大図をかくことができんだね。

この考え方なら、三角形と四角形だけではなく、どんな多角形でも拡大図をかくことができるね。

図形の１つの点を中心にして、中心からの距離を伸ばすことによって拡大図をかくことができるということは、その逆の縮図もかくことができそうだね。

学習のまとめ

頂点Ｄに対応する頂点Ｇの見付け方
●コンパスを使って、頂点Ｇを見付けることができた（２倍の拡大図をかくことができた）。　

・コンパスを使ったということは、三角形ＥＦＧをつくったということ。（三角形ＡＣＤの拡大図）

四角形は２つの三角形に分けて、それぞれの拡大図をつくることによって、拡大図をかくことができる。

●対角線を使って、頂点Ｇを見付けることができた（２倍の拡大図をかくことができた）。

・対角線を使ったということは、四角形ＡＢＣＤを三角形ＡＢＤと三角形ＢＣＤに分けたということ
・頂点Ｂを中心にして、２つの拡大図をかいたということ

四角形の１つの頂点を中心にして、中心からの距離をそれぞれ伸ばすことによって、拡大図をかくことができる。
○中心にする点は、頂点に限らないかもしれない。
○縮図も同じようにかくことができそう。
○四角形について考えたけれど、五角形や六角形などの多角形でもこの考えを使うことができそう。　　

評価問題

四角形ＥＢＦＧは、四角形ＡＢＣＤの２倍の拡大図です。元の四角形ＡＢＣＤをかきましょう。

子供に期待する解答の具体例

本時の評価規準を達成した子供の具体の姿

図形を構成する要素及び図形間の関係に着目し、見いだした拡大図の性質を基にして、１つの点を中心にした方法で縮図を作図している。

感想例

図形の１つの点を中心にして、中心からの距離を伸ばすことによって、拡大図をかくことができることが分かりました。
拡大図から元の図を考えるということは、縮図をかくということだと考えました。
１つの点を中心にして拡大図を作図する方法は、角が共通しているから、簡単に作図することができると思いました。
同じように中心にする点をとって、縮図もかいてみたいです。
対角線のアイデアはすごいと思っていましたが、よく考えてみると、対角線を使うことは２つの三角形に分けていることになるので、コンパスの考えにもつながっているんだなと思いました。
拡大図と縮図は別のものだと思っていたけど、違うのは倍率だけなんだなと思いました。合同な図形も、「１倍の拡大図」と言えるかもしれないと思います。