小6算数「拡大図と縮図」指導アイデア《拡大図と縮図の意味と性質》
執筆/新潟県新潟市立上所小学校教諭・佐藤諒子
監修/文部科学省教科調査官・笠井健一、新潟県新潟市立新津第一小学校校長・間嶋哲

目次
単元の展開
第1時(本時)対応する辺の長さを簡単な比で表すことで、拡大図と縮図の意味と性質を理解する。
▼
第2時 拡大図と縮図について、対応する辺の比から、何倍の図であるかを考える。
▼
第3時 方眼紙を利用した、拡大図と縮図のかき方を考え、実際にかく。
▼
第4時 辺の長さや角の大きさを使った拡大図のかき方を考える。
▼
第5時 辺の長さや角の大きさを使った縮図のかき方を考える。
▼
第6時 一つの頂点を中心とした拡大図・縮図のかき方を考える。
▼
第7時 任意の点を中心にした拡大図・縮図のかき方を考える。
▼
第8時 縮尺の意味と表し方を理解する。
▼
第9時 身の回りの長さの測定に縮図の考えを活用して、実際の長さを求める。
▼
第10時 学習内容の習熟・定着を図る。
本時のねらい
拡大図と縮図の意味と性質を理解することについて、当たりくじ(拡大図・縮図の関係になっている図形)の共通点や、はずれくじとの相違点を考える活動を通して、対応する角の大きさが等しいことと対応する辺の比がすべて等しいことが条件であることに気付くことができる。
評価規準
拡大図・縮図の意味と性質を使って、自分でも当たりくじ(拡大図・縮図の関係になっている図形)を考え、説明することができる。
本時の展開

くじ引きをしよう。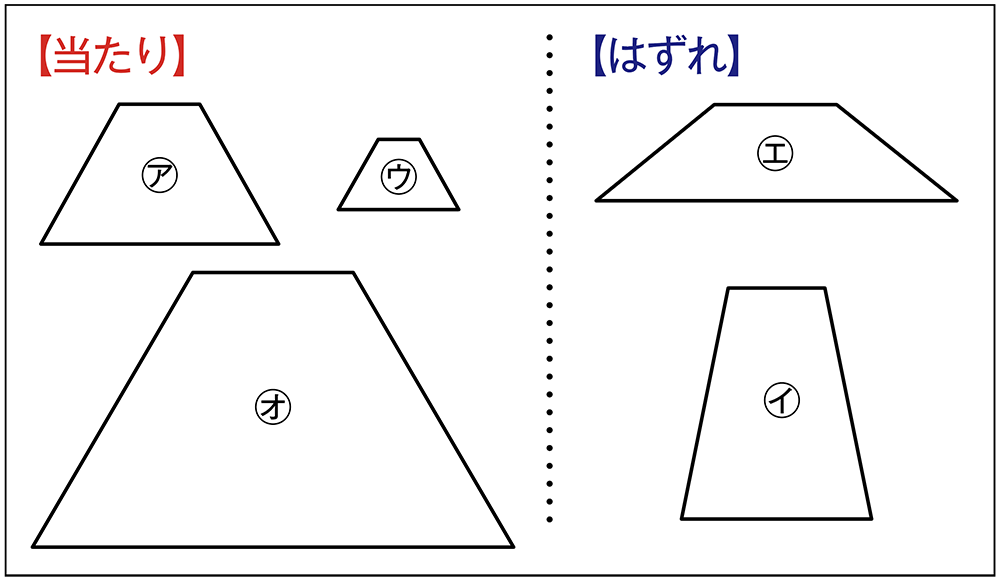
運試しに、くじ引きをしましょう。
当たりが出た!
はずれだった。
当たりの図形は、見た目がそっくりだな。
何かきまりがあるのかもしれない。

当たりくじには、何かきまりがあるのかな。
見通し
きまりを見付けるために、やってみたいことや知りたいことはありますか。
重ねてみたいです。見た目が似ているのは、角度が同じだからかもしれないから。
辺の長さも関係するかもしれません。
では、まずは重ねてみましょうか。
どの角もピッタリです。
やっぱり! 当たりくじは対応する角の大きさがすべて等しいんだ。
対応する角の大きさがすべて等しいものは、当たりくじになるのですね。まだ、くじが残っていました。引いてみますね。
当たりかな。はずれかな。
大変です。当たりかはずれを書き忘れたようです。㋕はどちらでしょうか。

見た目は、当たりくじよりも横に長いから、はずれに見えます。
当たりくじと重ねてみて、角の大きさが等しければ当たりかもしれないです。

対応する角の大きさが等しくなることに気付いた時点で、もう一度くじ引きをし、㋕のように、対応する角の大きさが等しいが、辺の長さの比は等しくないものを提示します。そうすることで、なんとなく見た目で判断していた子は、数値から根拠を見いだそうとしたり、辺の長さに着目できていない子は、長さに共通点があるのではないかと考え始めたりして、子供の思考を揺さぶることができます。
すべての角の大きさは等しいですね。これは当たりくじでよいですね。
う〜ん、でも、なんとなく違う気がします。
辺の長さを教えてください。
長さは、それぞれこうなります。
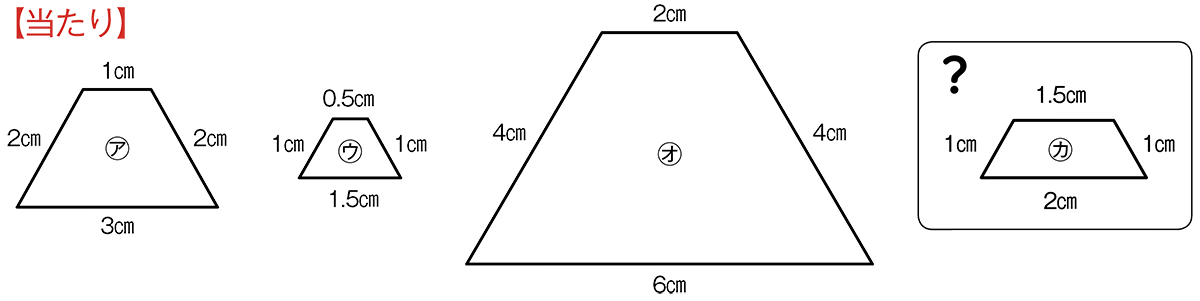
あれ、㋔は㋐の2倍になっているのかな。
長さに何か関係性がありそうなんですね。㋕が当たりくじかはずれくじか、また、その理由をノートに書きましょう。
自力解決の様子
A つまずいている子
- 辺の長さの関係を見いだせず、対応する角の大きさだけに着目し、すべての角の大きさが等しいことを根拠に、㋕は当たりくじであると考えている。
B 素朴に解いている子
- 当たりくじは、角の大きさと辺の長さの両方が関係することが分かり、1か所以上の辺の長さの関係(2倍や[MATH]\(\frac{1}{2}\)[/MATH]倍など)に気付いて、㋕ははずれくじであると考えている。
C ねらい通り解いている子
- 当たりくじは、対応するすべての角が等しく、対応する辺の長さの比もすべて等しくなることに気付き、㋕ははずれくじであると考えている。
学び合いの計画
イラスト/横井智美

