【プログラミング授業実践レポート】小６算数「関係を見つけて」

授業改善

2020.02.11

プリント

めあてを掲示

授業の冒頭は、ペアトークでウォームアップ。教室（パソコン室）の中央に集まって床に座り、「二学期で楽しかったこと」についてペアトークします。「あと30秒くらいで授業が始まります」との先生の言葉で、授業モードに切り替わります。

今日は算数の『関係を見つけて』の授業です。２つの数のなんらかの関係を見つけます。（吉冨先生）

マッチ棒のイラストを「綿棒？」と言った子に先生も反応したりしながら、和やかに授業が始まりました。

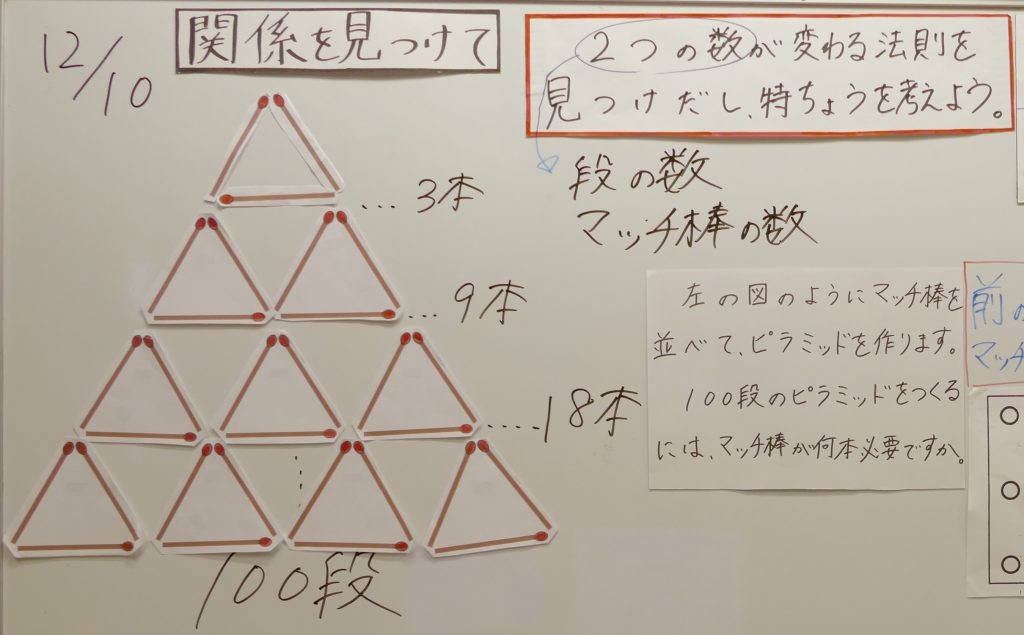
マッチ棒をならべて三角形をつくります。ピラミッド状に２段、３段にしたときの全部のマッチ棒の本数を、子供たちは図を見ながら数えて、「9本」「18本」という声が一斉にあがります。

「100段あったら？」との問いにもすかさず「300本」と答えたＡ君に、先生は「ほんとに？」と問い返します。

「う～ん…」といった表情の子供たち。そこで今日のめあてが掲示されます。

今日は、全部のマッチ棒の数と、１段、2段、３段…、という2つの数の関係を考えながら、100段だと何本になるかということを考えていきましょう。

［めあて］
２つの数が変わる法則を見つけだし、特ちょうを考えよう。

「この、２つの数って何だろう？」と問う吉冨先生。

「段と本数」と答えたＢ君は、「もうちょっと具体的に言ってみようか」と先生に促され、「段の数とマッチ棒の数」と答え直します。

今日のめあてを示した板書
（※この写真は授業終了後に撮影したものです）
＊クリックすると別ウィンドウで開きます

【動画】初発からめあてまでの授業の流れ

「2つの数の関係性を見つけるには、どうしたらいいかな？」とさらに問う吉冨先生。

子供たちからは、意見がなかなか出てきません。そこで、ペアで相談することにしました。

【授業者による解説】
予想したよりも子供たちの理解に時間がかかり、「ん？」という表情の子がけっこういました。たくさん発言を聞いた中から整理していく展開をイメージしていたけれども、意見があまり出てこないので、急遽ペアトークを取り入れることに。「どうしようか？」と子供たちに聞くと「ペアトーク」と子供たちの方から出てきました。常にどうしたいかを子供たちに問うことを心がけています。

「何を使えばできそう？　比例のときどうしたっけ？　何か使わなかったっけ？」と、考えるヒントを与える吉冨先生。すると子供たちから、「電卓」「グラフ」…、やがて「表」という言葉が出てきました。

「こんな感じの表かな？」と、表を掲示する吉冨先生。

「これを使えばできそう？」との問いかけに自信ありげな子供たち。難なく５段目までの数が入ります。

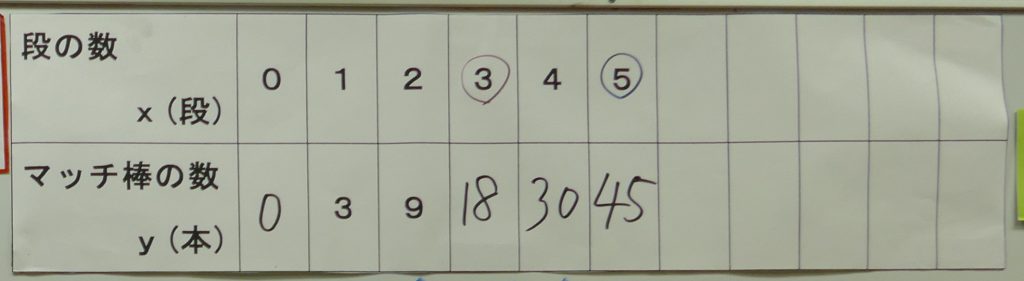
「表には見方があったよね。2種類あったね」と問われると、子供たちは「縦と横！」とすぐに答えます。今回はどっちを見るのかとの問いにも「横！」と即答。

「横に見ていったら法則を見つけられそうかな？　やってみる？」との提案に、やる気顔の子供たちです。

ワークシートで考える

「どれくらいの時間がほしい？」と子供たちに問いかけ、３分と決めてタイマーをセット。「スタート！」の声で、ワークシートにとりかかります。

ワークシートに書き込む子 — ワークシートに書き込む児童。まだパソコンには一切ふれていない。

子供たちがワークシートに取り組む中を机間巡視して、一人一人にひそひそ声で

ここからここ、いくつ増えてる？
ここの関係性を見つけよう。
その先どうなってる？　全部書いてごらん。
なんでこうなったか仕組みを言葉で書いてみよう。

とヒントを与えていきます。

ある程度経過したところで、「一人でできるかな？　ちょっと難しい？　ペアで相談してやってみようか。イスを移動して班で共有してもいいよ。」と指示を出しました。

３分のタイマーが鳴ると、「まだ時間が欲しい班は大きく手をあげて」と声かけし、１分延長です。

子供たちの様子を見回る吉冨教諭 — 声をかけながら子供たちの様子を見回る吉冨先生

「うん、おもしろいね。あ～～なるほどね。そういうことか。すごいね！」

子供の説明に反応する吉冨先生。

「そろそろいいですか？　えんぴつとワークシートを持ってまた真ん中に集合してください」ここでも班でまとまって集まるように言います。

考えを共有していきたいんだけど、「こんなヒミツ見つかったよ」って人いますか？

「1段のときは３本増えてて…」と説明しだした子には、「1段のときというのは？　０から１段のときということかな？」と、論理的な説明になるように促します。

「増えている数は、みんな３の段になっている」といった発見も出てきたところで、

「同じだよ」という人はいますか。では、Cさん、自分の言葉で教えてください。

と子供の発言をつなげていきます。

段の数が増えていく毎に、三角形が1個増えるから、ひとつの三角形に必要なマッチの本数が3本で、だからプラス３ずつ増えていて、増えている数が３の段の数になる。（Cさん）

マッチ棒の数は、前の段より、たす３、たす６と増えていくから、100の段になると…。んーと…。（D君）

今、D君が「んー？」となっていましたね。では、D君がどういうことを言いたいのか、近くの人とちょっと共有してみてください。

と、交流して考えさせる吉冨先生。「Ｄ君が言いたいことがわかった人いる？　自分の言葉で説明してください」と問いかけ、別の子供に説明させます。

続けて「他の考えも出ていたよね。他の考えを言える人、共有しよう」と問いかけ、E君が発言します。

段が１つ増えるごとに、『３×X』の分だけ増える！（Ｅ君）

「X」は何のことなのかを問われると、すぐさま「段！」と答えた子供たち。

『３ × 段の数』をすればいいってことだね。そうすれば全部のマッチ棒の数が求められるのかな。（わざと間違う吉冨先生）

ほかの意見もあったよねと指摘すると、するとＦ君が「前のＹの数＋３×X 」と言った後、みんなに解説を始めました。

5段のときは、Ｙが30のところを見て、30＋３✕５をすればいいです。（Ｆ君）

「30」は何を表すのかを問い返し、「出したい数の前の段のマッチ棒全部の数」と言葉でわかりやすく説明するＦ君。多くの子供がうんうんと頷いている様子が見られます。

ここでワークシートに戻り、下部分にある問題に記入してから、ペアで確認し合います。

T「さあ、3段になると前の段に加えて？」
C「３×３」
T「なんで３×３？」
C「2段の下にある…」
T「こういうこと？」T「この3は何？」
C「段」
T「じゃあ、5段になると、4段目のマッチ棒の数に加えて？」
C「３×５」
T「この5は？」
C「段数」

つまり、段の数が1増えるごとに…

子供たちから「３×X 増えている。」と一斉に返ってきます。

ここで「言葉の式にするとどうなる？」と問う吉冨先生。

「決まった数３✕段数」との子供たちの発言に、「よし、じゃあこれでOKだね。『マッチ棒の数＝３✕段の数』」と、またもや早とちりした誤答を吉冨先生が口にします。すると、「ダメー」と子供たちがすぐさま反応。理由を問われると、「前の段のマッチ棒の数が必要だから」と返します。

で、今回求めたいのは何段？

という初発に立ち戻り、子供たちは「100段」と反応。

求められそう？

ここで、再びペアで交流。マッチ棒全部の数がどう増えていくかの仕組みはわかったので、100段めの数の求め方をペアで話し合って考えますが、なかなか解決策が出てきません。

「何で悩んでるのかな？」と聞く吉冨先生。「できるっちゃ、できるんだけど…」というつぶやきに、「じゃあやってみたらいいじゃない」と吉冨先生が呼びかけます。それに対し「でも１時間じゃ終わらない」という子供のつぶやきがもれました。

吉冨教諭が理由を問うと、

かけてたしてをくりかえすから。100段あるから100回計算しなくちゃいけない。

という意見が出てきました。

100回も！…じゃあ、あきらめようか。やめようか。どうする？

と吉冨先生のけしかけた言葉に、子供たちは「やだ！」

一度は「気合いでできる！」と元気よく言ったＧ君ですが、「でもやっぱり時間が足りないかも…」と弱気に（笑）

するとどこからともなく、子供たちから「プログラミング」「スクラッチ」という言葉が出てきました！　

じゃあプログラミングを使ってやってみようか。

【動画】100段までの計算をするためにプログラミングを活用するまでの流れ

【授業者による解説】
こちらから提示するのではなくて、プログラミングならできるんじゃない？　スクラッチならできそう、という言葉が子供たちから出てきてほしいなという思いを持ちながら授業を行いました。100回計算するのは大変すぎるよね、と言ったところで出てきたので、そこでやってみる？とつなげて授業を展開できました。