小２算数「大きい数のたし算とひき算」指導アイデア《繰り上がりが２回ある２位数＋２位数＝３位数の筆算の仕方》
執筆／さいたま市立桜木小学校教諭・黒須直之
監修／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
単元の展開
第１時 ２位数＋２位数＝３位数（百の位への繰り上がりあり）の筆算の仕方を理解し、その計算ができる。
▼
第２時（本時）２位数＋２位数＝３位数（十、百の位への繰り上がりあり）や２位数＋１・２位数＝３位数（百の位への波及的繰り上がりあり）の筆算の仕方を、数の見方や既習の加法筆算の仕方を基に考え、説明することができる。
▼
第３時 学習内容を適用して、問題を解決する。
▼
第４時 ３位数－２位数（百の位からの繰り下がりあり）の筆算の仕方を理解し、その計算ができる。
▼
第５時 ３位数－２位数（十、百の位からの繰り下がりあり）の筆算の仕方を基に考え、説明することができる。
▼
第６時・第７時 ３位数－１・２位数（十、百の位からの波及的繰り下がりあり）の筆算の仕方を理解し、その計算ができる。
▼
第８時 ３位数＋１・２位数（百の位への繰り上がりなし）や３位数－１・２位数（百の位からの繰り下がりなし）の筆算の仕方を理解し、その計算ができる。
▼
第９時 ３位数＋１・２位数（百の位への繰り上がりあり）や３位数－１・２位数（百の位からの繰り下がりあり）の筆算の仕方を理解し、その計算ができる。
▼
第10時 学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り、価値付ける。
本時のねらい
２位数＋２位数＝３位数（十、百の位への繰り上がりあり）や２位数＋１・２位数＝３位数（百の位への波及的繰り上がりあり）の筆算の仕方を、数の見方や既習の加法筆算の仕方を基に考え、説明できるようにする。
評価規準
既習を基に、２位数＋２位数＝３位数（十、百の位への繰り上がりあり）や２位数＋１・２位数＝３位数（百の位への波及的繰り上がりあり）の筆算の仕方を、式や言葉などを用いて、数の仕組み（10進位取り記数法）に着目して考え、説明している。（思考力・判断力・表現力）
本時の展開
※問題場面で２位数＋２位数＝３位数（十、百の位への繰り上がりあり）について確認して、適用問題で、２位数＋１、２位数＝３位数（百の位への波及的繰り上がりあり）について取り扱います。
85円のチョコレートと39円のグミを買います。ぜんぶでいくらになるでしょうか。
※85と39の数字は封筒に入れておき、問題場面の提示と合わせて子供たちに見せるようにする。
全部でいくらになるか知るために計算するためにはどんな式になりますか。
85＋39で求められると思います。
式は85＋39になるのですね。今日は、この85＋39の筆算について考えていきましょう。この計算の答えは、全部でいくらくらいになるでしょうか。
100円より多いと思います。
80＋40だと120だから120円よりちょっと多いくらいじゃないかと思います。
なるほど。今まで習った計算を使って予想したのですね。ところで、昨日習ったことと比べると、今回の式は何が違うでしょうか。
10の位だけじゃなくて、１の位も繰り上がりがあります。
10の位も１の位も繰り上がるから、繰り上がるが２回ある筆算です。
繰り上がりが２回ある筆算になりそうなのですね。どうやったらできそうでしょうか。
筆算だから位を揃えて書かないとだね。
昨日みたいに図を使って、考えればできるんじゃないかな。
２回も繰り上がりがあったら、よく分からなくなっちゃいそうで心配。
何かよいアイデアはないですか。
一の位から順番に計算していけば大丈夫じゃないかな。
前みたいに繰り上がった数を小さく書いておけばよいんじゃないかな。
いろいろなアイデアが出ましたね。では、繰り上がりが２回ある筆算の仕方に今までに習ったことを生かして考えてみましょう。
繰り上がりが２回ある筆算の仕方を考えよう。
見通し
前の時間にやったように、まずは位を揃えて書いて、一の位から計算してみればできるんじゃないかな。
繰り上がった数を書いておけば、繰り上がりが２回あっても間違えずに計算できそうよ。
前の時間にやった、図を使って筆算の仕方を説明してみたいな。
自力解決の様子
Ａ つまずいている子
十の位に繰り上がった数を足さずに、計算してしまっている。
筆算の例
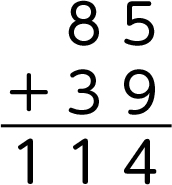
Ｂ 素朴に解いている子
補助数字を用いて、十の位に繰り上がった数を足して、計算をしている。
筆算の例
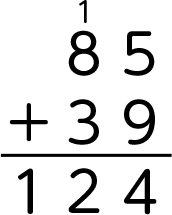
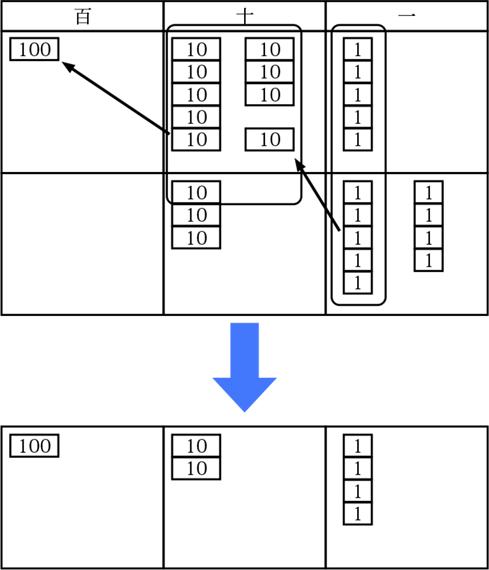
Ｃ ねらい通り解いている子
補助数字を用いて十の位に繰り上がった数を足して計算したり、図と関連付けて考えたりしている。
筆算の例
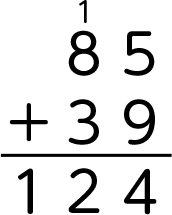
学び合いの計画
問題場面
本時の問題場面でのねらいは、２位数＋２位数＝３位数（十、百の位への繰り上がりあり）の筆算の仕方を、数の見方や既習の加法筆算の仕方を基に考え、説明できるようにすることです。
子供が説明する際には、筆算のプロセスだけでなく、図と関連させながら、十進位取り記数法の理解を深めることが大切です。
前時で百の位への繰り上がりがある計算の筆算を学習していますが、まだ計算の説明については「筆算の手順についての説明」が主であり、なぜ次の位に繰り上がるのかという仕組みについてまでしっかりと発表できる子供は多くないでしょう。
また、十の位への繰り上がった数の処理についても、まだ理解が十分ではないことが考えられるので、本時では、「繰り上がった数を含めた十の位の計算の説明」に焦点を当てて、式や言葉などを用いながら、数の仕組み（十進位取り記数法）に着目して考え、説明する活動を行うようにしていきます。
子供のつまずきを考慮すると、補助数字を用いた筆算の指導が効果的です。補助数字の扱いについても改めて確認をしながら、説明できるようにしていきます。その際、学級の実態に合わせて、少人数のグループで説明し合ったり、１人１台端末でノートの写真や図を共有して話し合ったりするなどの工夫をするのも効果的です。
まとめ
まとめでは、２回繰り上がる筆算についての方法を整理していきます。その際、既習事項と関連させ、筆算の仕組みについて改めて確認しながら、まとめていくようにします。学習のつながりに目を向けて、既習事項を生かしていく力を計画的に培っていくことが大切です。
適用問題
適用問題では、２位数＋１・２位数＝３位数（百の位への波及的繰り上がりあり）を扱います。そのため、本時の問題場面で理解が十分ではない子供に対する支援も必要になってきます。適用問題の数を学級の子供たちの状況に合わせて調整するといった工夫をして、個に応じた指導が実現できるように配慮するといった対策をすると効果的です。
知識・技能については、次時の「学習内容を適用して、問題を解決する活動」を通して、徐々に身に付けていく指導が大切です。
ノート例
Ａ つまずいている子
Ｂ 素朴に解いている子
全体発表とそれぞれの考えの関連付け
85＋39の筆算の計算についてみんなで確認してみましょう。
＜Aさん＞ まず、位を揃えて書きました。その後、一の位から計算しました。
前の時間に習ったことを生かしたのですね。Aさんは、一の位の計算をした後はどうやっていたでしょうか。
＜Bさん＞ ５＋９で14だったから、十の位に１を繰り上げています。
Bさんが言ってくれたのは、Aさんの筆算で言うとどこでしょうか。指をさしてみてください。指をさしている人が多いのはここかな。（補助数字を指さす）この１は何でしょう。
これは、一の位から繰り上がってきた１だと思います。
一の位で10になったのを十の位に繰り上げたから、そこに１があるんだと思います。
なるほど。では、この１は一の位から繰り上がった10を表しているというわけですね。
＜Cさん＞ そうそう。その後、１と８で９にして、９＋３をしたんです。
１と８で９とはどういうことですか。こちらの図で説明してみてください。
＜Cさん＞ 一の位を計算すると５＋９で14になって……、もともと十の位に８があります。その８と繰り上げた１を足しました。(黒板の図で)
なるほど。図を使って、友達とCさんが説明したことを確認してみましょう。
※小グループでの話合いを行った後、十の位の計算について確認を行う。
グループでの話合いで、繰り上げた数をどうやって計算したらいいか分かりましたね。
はい。最後に９＋３をして、百の位に１を繰り上げて答えを求めました。
全部で123円。予想の120円に近かったね。
２回繰り上がりがありましたが、どのように筆算しましたか。
まず、位を揃えて書いて、一の位から計算しました。
繰り上がった数を忘れないように小さく書いておきました。
あと、２回繰り上がりがあっても、10を超えたら次の位に１繰り上げて計算すればいいです。
なるほど。昨日までの筆算とやり方に違いはありましたか。
計算の仕方はほとんど同じでした。同じようにやればできました。
では、２回繰り上がりがある計算はどのようにすればよいか、まとめましょう。
位を揃えて、一の位から順番に計算する。
繰り上がった数を忘れないようにする。
図を使うと分かりやすく説明しやすくなる。
２回繰り上がりがある筆算も今まで習ってきたことを使って説明しながら解決できましたね。
●繰り上がりが２回ある筆算でも、位を揃えて、一の位から順番に計算していけば、今までと同じように計算できる。
●繰り上がった数を次の位に書いておくと間違いが少なくなる。
●図を使うと筆算のやり方が説明できる。
評価問題
ワークシート（ダウンロード可）
ダウンロードはこちら＞＞
子供に期待する解答の具体例
感想例
- 繰り上がりが２回ある計算も、前の時間と同じようにできることが分かった。図でも説明できた。
- 繰り上がった数を次の位に書いておくと、繰り上がりを忘れにくいことが分かった。
- ３桁のたし算も同じようにできるんじゃないかなって思った。
- ひき算の筆算もやってみたい。
板書例
※評価問題はスクリーンなどで、ワークシートを別途提示しながら行う。
イラスト／横井智美
【関連記事】
1人1台端末時代の｢教科指導のヒントとアイデア｣シリーズはこちら！
・小１算数「ちがいはいくつ」指導アイデア《求差の意味》
・小１算数「のこりはいくつ」指導アイデア《減法の意味や式の表し方（求補の場面）》
・小１算数「ふえるといくつ」指導アイデア《加法の意味を考える》
・小１算数「あわせていくつ」指導アイデア《２つの数量の合併の加法の意味や式の表し方の理解》
・小１算数「いろいろな形」指導アイデア《立体の面を写した絵描き遊び》
・小3 国語科「漢字の広場④」全時間の板書＆指導アイデア
・小1 国語科「かん字のはなし」全時間の板書例＆指導アイデア
・小5理科「ふりこの運動」指導アイデア
・小3理科「電気の通り道」指導アイデア
・小5理科「人のたんじょう」指導アイデア
>>もっと見る
