小6算数「場合の数（1）」指導アイデア
執筆／埼玉県公立小学校教諭・清水則仁
編集委員／国立教育政策研究所教育課程調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
（本時１／６ 組み合わせ）
ねらい
順列について、落ちや重なりがないように調べる方法を考え、その方法を理解する。
評価規準
列について、落ちや重なりがないように、図や表を用いたりして、順序よく筋道立てて考え、調べている。（数学的な考え方）
問題
あつしさん、かいとさん、さとしさん、たつきさんの４人でリレーのチームをつくります。
４人で走る順番の決め方を全部書きましょう。全部で何通りあるでしょうか。
全部で何通りになるか、どのように調べたらよいでしょう。
思いつくだけ書き出したらよいと思う。
でも、大変だし、うまく全部書き出せるかなあ。
順番に書き出したらどうだろう。
なるほど。では、最初にあつしさんが走るとすると、どんな順番が考えられますか。
例えば、①あつしさん、②かいとさん、③さとしさん、④たつきさんです。
すべての場合の中で、あげ忘れているときを「落ち」と言い、逆に、同じものを重ねてあげてしまうことを「重なり」と言います。 では、落ちや重なりがないように調べて、全部で何通りになるか求めてみましょう。
本時の学習のねらい
４人でリレーを走る順番を、落ちや重なりがないように調べる方法を考えよう。
見通し
子供の発言から、記号化すると数えやすいこと、１つずつ固定しながら考えると、手際よくできそうなことを引き出します。
自力解決の様子
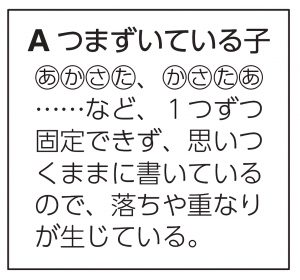
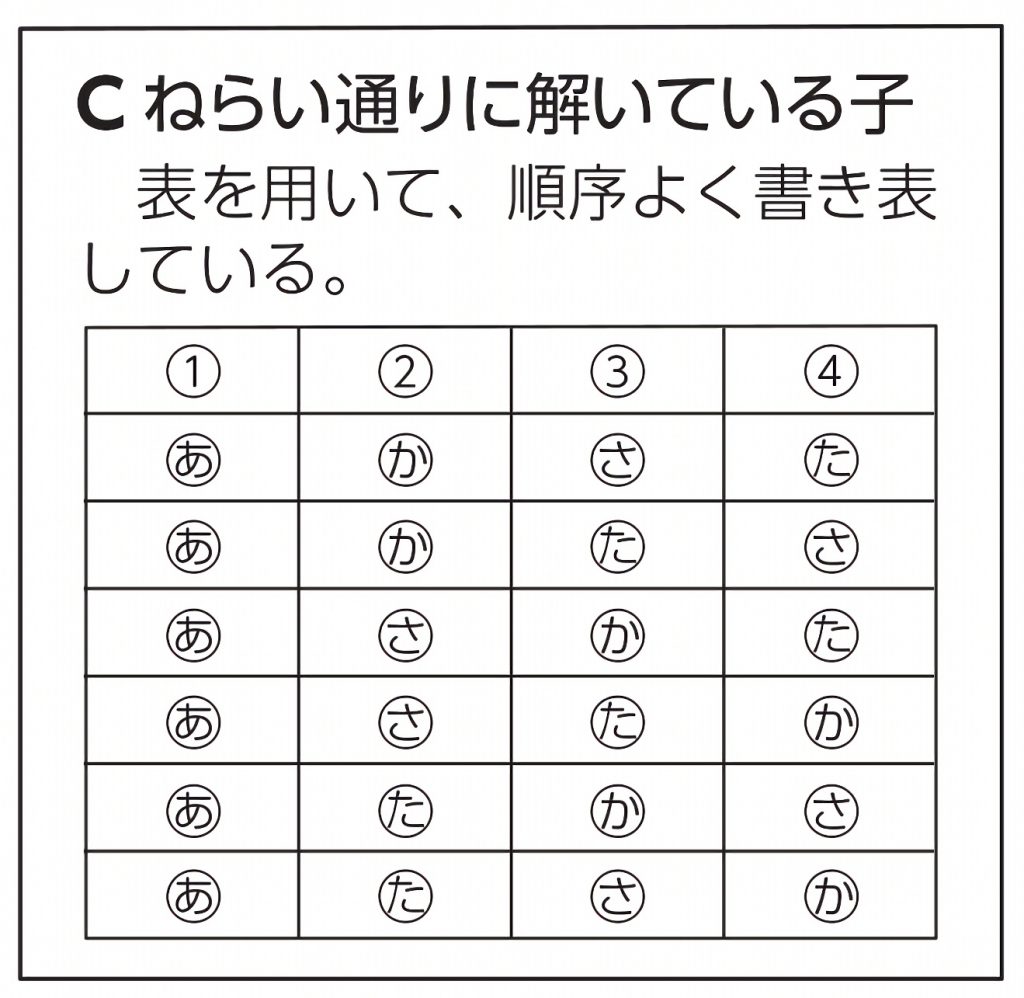
学び合いの計画
本時は、単元の導入の「並べ方（順列）」の学習なので、明確な既習事項があるわけではありません。自分なりのやり方で工夫して求める活動を通して、落ちや重なりがなく、より簡単で便利な方法で求めていくことで、思考力や表現力を育てます。
これらのやり方の比較検討の際、より簡単な書き表し方だけに話合いの視点をおくと、名前の記号化や省略の工夫、色分けなど、視覚的な方法の話合いになってしまうことがあります。
そのため落ちや重なりなくあげる工夫を中心に話し合うことにより、第１走者をまず固定し、第２、第３、第４走者と順番に書き出すという方法を、共通のものとしてまとめるようにします。
なお、記号化の工夫については、簡単に扱うとよいです。また、子供のやり方を生かし、樹形図の書き方を理解できるようにします。さらに、考え方を統合していく中で、式化についても理解できるようにしましょう。
ノート例
全体発表とそれぞれの考えの関連付け
どのようにしたら、落ちや重なりがなく調べられましたか。
ばらばらに書き出すと分からなくなってくるので、一人ずつ順番に書き出してみました。
（C1 からC3 までに説明させる）
どの考えも、最初にあつしさんを先頭に決め、２番目、３番目、アンカーを順に考えているね。
このように順々に書き出すと、落ちや重なりがなくあげられますね。この図を基に、式で解いた人がいたのですが、どんな式を立てたのでしょうか。
４×３×２×１だと思います。わけは、先頭になる人は４人います。第２走者は第１走者を除いて３人です。同じように第４走者まで考えると４×３×２×１（通り）となるからです。
表や図を使うと分かりやすく、式にも結び付けやすいですね。また、C3 のような図を樹形図と言います。
では、本時のまとめを書きましょう。
評価問題
「1」、「2」、「3」、「4」の４枚の数カードを使って、４けたの整数をつくります。何通りの整数ができるでしょうか。
子供に期待する解答の具体例
図や表を用いて解いている。
千の位が３や４の場合もあるので、24 通り。
本時の評価規準を達成した子供の具体の姿
- 千の位から順に数を決め、24 通りの整数を求めることができる。
- 図や表、式を用いて、24 通りの整数を求めることができる。
■6年算数 場合の数（2）へ続きます。
イラスト／やひろきよみ 横井智美
『小六教育技術』2018年12月号より
