小2算数「かけ算(2)」指導アイデア(1/11時)《6の段の九九の構成と理解》
執筆/東京都渋谷区立西原小学校主任教諭・網本幸代
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時(本時)6の段の九九を構成する。乗数が1増えると、積は被乗数分だけ増えることを理解する。
▼
第2時 6の段の九九の呼称を知り、唱える。6の段の九九を用いて、問題を解決する。
▼
第3時 7の段の九九を構成する。7の段の九九でも、乗数が1増えると、積は被乗数分だけ増えることを理解する。
▼
第4時 7の段の九九の呼称を知り、唱える。7の段の九九を用いて、問題を解決する。乗数の交換法則が成り立つことに気付く。
▼
第5時 8の段の九九を構成する。8の段の九九の構成を通して、答えの増え方や交換法則に気付く。
▼
第6時 8の段の九九の呼称を知り、唱える。8の段の九九を用いて、問題を解決する。
▼
第7時 9の段の九九を構成する。9の段の九九の構成を通して、答えの増え方や交換法則に気付く。
▼
第8時 9の段の九九の呼称を知り、唱える。9の段の九九を用いて、問題を解決する。
▼
第9時 1の段の九九を構成する。1の段の九九の呼称を知り、唱える。1の段の九九を用いて、問題を解決する。
▼
第10時 問題文の仕組みを読み取って加法や減法・乗法の演算決定をし、乗法の理解を深める。具体物の操作を基に、解き方や絵や図、式や数字、言葉を使って分かりやすく説明する。
▼
第11時 学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。
本時のねらい
かけ算の意味やかけ算の性質を用いて、6の段の九九を構成することができる。
評価規準
乗法の意味や性質を用いて、乗法九九を構成しようとしている。かけ算は乗数が1増えると、積は被乗数分だけ増えることに気付いている。
本時の展開

チーズが入っているはこがあります。1はこに、□こずつ入っています。はこの数が1、2、3……とふえていくときの、チーズの数をしらべましょう。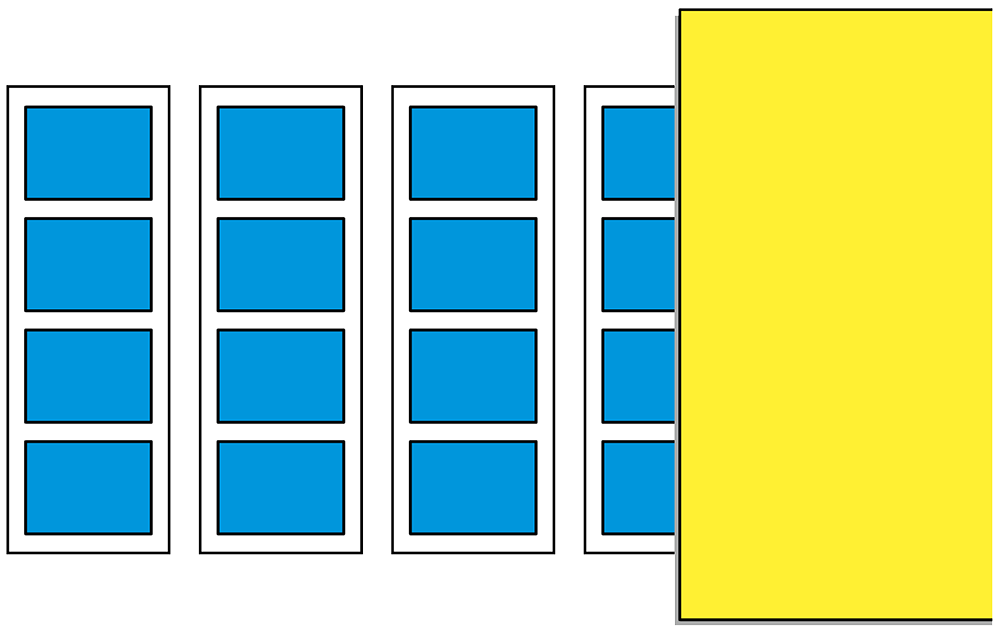
1箱にいくつ入っているのかな。
4つずつ入っています。
4個ずつ入っていたら、4の段でチーズの数が分かります。
なぜ4の段だと思ったのですか。隣の友達に説明してみましょう。
もしも1箱に4個ずつ入っていたら、チーズは4個ずつ増えていきます。4のまとまりがいくつあるかということだから、チーズが1箱だったら4×1=4、2箱だったら4×2=8、3箱だったら4×3=12……になるから、4の段で答えが出ます。
そうですね。4個ずつ増えると、4の段で答えが出せそうですね。次の箱は、チーズが6個ずつ入っています。
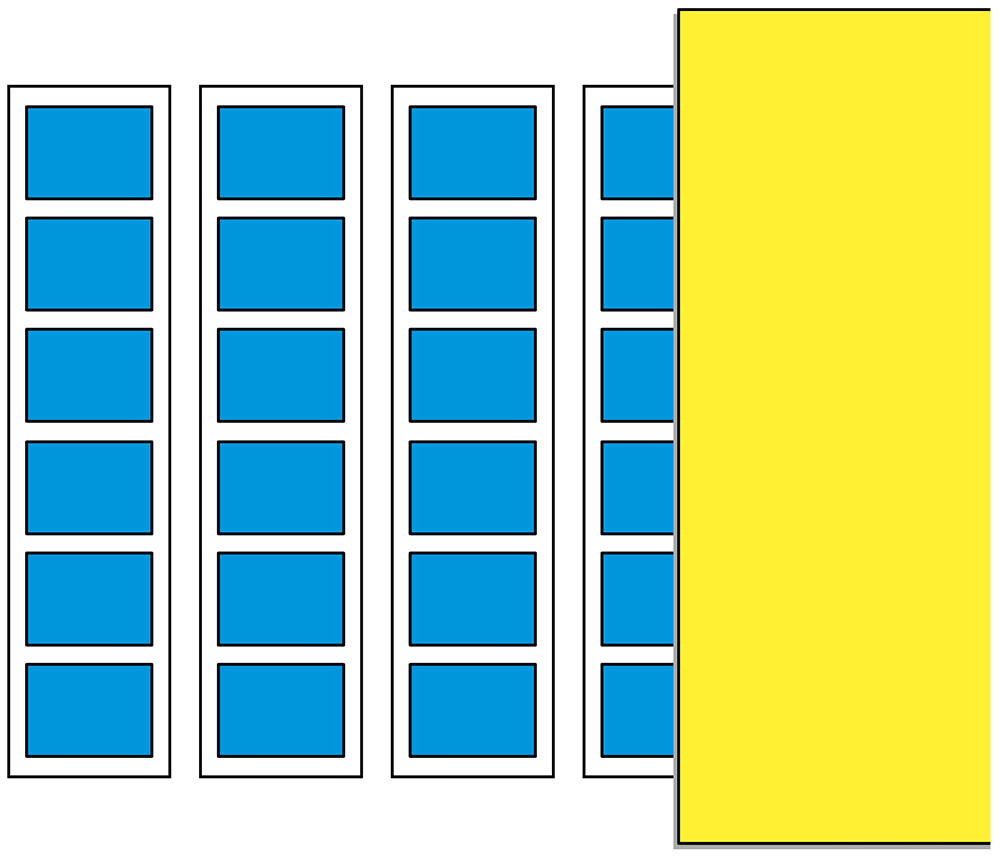
6個ずつということは、6の段だ。
6の段の九九はつくれそうですか。
4の段と同じようにすれば……。
チーズは6個ずつ増えていくから。
たし算を使えば……。

どうすれば、6の段がつくれるかな。
自力解決の様子
A つまずいている子①
1つ分×いくつ分が捉えられず、乗数と被乗数を逆に書いている。
1×6=6
2×6=12
3×6=18
4×6=24
A つまずいている子②
途中まで書けているが、続きが分からず手が止まっている。
6×1=6
6×2=12
A つまずいている子③
式は書けているが、答えを間違えている箇所がある。
6×1=6
6×2=12
6×3=19
6×4=25
B 素朴に解いている子
式も答えも正しく書けている。「6+6+6+6」という方法で答えを求めている。
6×1=6
6×2=12
6×3=18
6×4=24
C ねらい通り解いている子
式も答えも正しく書けている。かける数が1増えると、答えはかけられる数だけ増えることに気付いている。
6×1=6
6×2=12
6×3=18
6×4=24
学び合いの計画
6の段の九九を構成するとき、子供はすでに2~5の段の九九は構成した経験があります。
イラスト/横井智美

