小1算数「のこりはいくつ ちがいはいくつ」指導アイデア(3/10時)《のこりがいくつかしらべよう》
国立教育政策研究所教育課程調査官の監修による、教科指導のアイディアと授業のヒントをまとめた指導計画例です。次時の授業にお役立てください。
執筆/福岡県公立小学校教諭・田中智史
編集委員/国立教育政策研究所教育課程調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
単元名「のこりはいくつ」
本時のねらいと評価規準(本時の位置 3/ 10)
【本時のねらい】
2つの数量の求残の場面について、数量の関係に着目し、具体物を操作する活動を通して、減法の意味や式の表し方を理解する。
【評価規準】
2つの数量の求残の場面について、その意味を理解している。(知識・理解)
[問題場面] 7にんで、あそんでいました。3にんが、かえりました。のこりは、なんにんですか。
昨日は、5匹の金魚から2匹をとる問題でしたね。
ブロックをとって、残りを見つけたよ。
今日の問題は、昨日の問題と何か違うかな。
今日は、友達が7人で遊んでいます。
3人が帰りました。
昨日のお話と違うから、残りがいくつか調べるのは難しそうだね。
え? 昨日と同じようにできると思うな。
帰るのは初めてだから、できないよ。
どうすれば、残りが調べられるかな。
※この時間は、問題場面の比較から導入を行い、場面が違っても、前時と同じ操作で残りが調べられるかという問いに、焦点化していくようにします。
本時の学習のねらい
のこりが いくつか しらべよう。
【見通し】
・ブロックを7こ並べる。
・ブロックをとる。
・残ったブロックの数を数える。
昨日は、ブロックを使って調べられましたね。今日も、ブロ
ックを使って調べられそうかな。
ブロックを使ってできそう。
はじめは、7こ並べるんじゃないかな。
「帰りました」だから、ブロックをとればいいと思うな。
残ったブロックを数えれば、いいんじゃないかな。
では、ブロックを使って調べてみましょう。
【自力解決の様子】
A:つまずいている子
ブロックの操作で、問題場面をうまく表現することができない(ブロックを、10 個置くなど)。
B:素朴に解いている子
問題場面をブロックの操作で表現し、残りの数を見つけることができている。
C:ねらい通りに解いている子
問題場面をブロックの操作で表現し、残りの数を見つけ、操作の共通性に気付き、ひき算の式を書いている。
【自力解決と学び合いのポイント】

Aの子供に対しては、問題文の意味(最初は、7名しかいなかったことなど)を確認し、問題場面をブロックで表現できるようにしましょう。そして、操作の結果に対して、「帰った人は、どれかな?」「残って遊んでいる人は、どれかな?」等と投げかけ、減った数や残った数を意識することができるようにしましょう。
Bの子供に対しては、ブロックの操作の様子をノートに書くよう促しましょう。
【全体発表とそれぞれの考えの関連付け】
ブロックの操作を行った後は、黒板上で拡大ブロックを動かしながら、全体でブロックの操作を確認します。
(ブロックの操作を確かめた後)式はどうなるかな。今日は「帰りました」だけど、昨日と同じひき算でいいのかな。
「帰りました」だけど、同じようにブロックをとったから、同じでいいと思います。
今日も、ブロックの数が減ったから、ひき算でいいと思うよ。
「帰りました」でも、昨日みたいにブロックをとっているから、ひき算でよさそうだね。
前時の学習で行ったブロックの操作と、本時の学習で行ったブロックの操作を比較しながら、「帰った」場面でも、前時の場面と操作が同じことから、ひき算で答えを求められることを理解させます。その後、どのような式になるかを考えていきます。「式の3は、何の数かな」「式の4は、ブロックの図のどこのことかな」などと発問し、式の数字が、何を表すかをおさえておくとよいでしょう。
【ノート例】
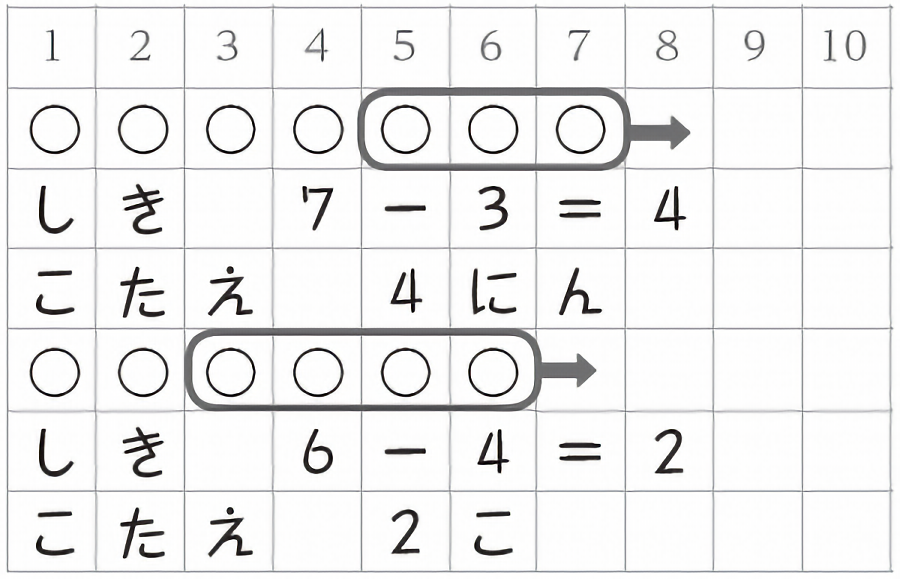
【本時のまとめ】
「かえりました」の問題も、ひき算で答えがわかる。
<評価問題>
ふうせんが、6こ ありました。4こ、とんでいきました。のこりは、なんこですか。ブロックで あらわしてから、しきと こたえを かきましょう。
<期待する子供の姿>
場面をブロックで正しく操作し、「6-4=2 こたえ 2こ」と、式で表現し、答えを求めることができる。
【子供の感想例】
「とんでいく」のも「帰る」のも、ブロックを同じように動かせばよいことがわかりました。
「とんでいく」も「帰る」の時と同じように、ひき算になることがわかりました。
単元名「ちがいはいくつ」
本時のねらいと評価規準(本時の位置7/ 10)
【本時のねらい】
2つの数量の求差の場面について、数量の関係に着目し、具体物を操作する活動を通して、減法の意味や式の表し方を理解する。
【評価規準】
2つの数量の求差の場面について、その意味を理解している。(知識・理解)
[問題場面] いぬは、ねこより なんびき おおいですか。

昨日の問題と、何か違うかな。
イラスト/佐藤雅枝・横井智美
『小一教育技術』2018年7/8月号より