子供自身が系統性に気付き、理解していくような授業づくりが大切【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #9】

前回、異分母分数のたし算の学習で、１学年からのたし算の学習をふり返り統合していく授業について、新潟市立上所小学校の志田倫明教諭に説明していただきました。今回はそのような学習の意義などについて、解説していただきます。

新しく得た視点でそれまでの学習を捉え直す

前回、異分母分数のたし算を学習する過程で、１学年からのたし算の学習をふり返り、統合していく授業について説明をしました。これは、まさにこの連載のねらいである「６年間の系統を意識した学習」で、それはとても大事なものです。例えば、簡単な分数のたし算は３学年の時点で学習をしています。そのときから、整数も小数も分数も単位が揃っているからたすことができるということを意識できるように指導し、そうしたことへの気付きを価値付けていくことが大事です。そのようにして、子供自身が系統性に気付き、理解していくような授業づくりが大切なのです。

前回の学習に続いてひき算の学習をしたのですが、実はその授業を終えた後、前回「２＋３は何が揃っているの？」と問いを投げてくれた子供が、ざっと次のような話をしてくれました。｢例えば、１年生のとき考えた３－２についてなんですけど、これを１円玉が３つと１円玉が２つと考えると、一緒じゃないですか？　だから単位としているのは『１』で､『１』が３つから『１』が２つを引いているから『１』が１つになります。でも10ー２になると10は10円玉が１つで『10』が１つと考えられるから､『１』が２つとは単位が違って、１ー２はできなくなる。けど、10を『１』が10こと考えると､『１』が10こから『１』が２つを引くと『１』が８つになって計算できます。やっぱり単位を揃えると計算できるということです。これは、通分すると計算できるのと同じことです」と。つまり、加法も減法も単位を揃えるという基本的な考え方は変わらないと統合していったわけです。

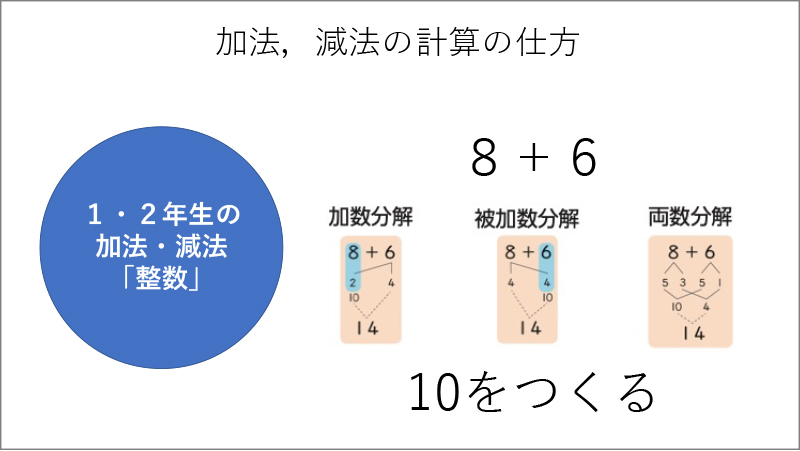
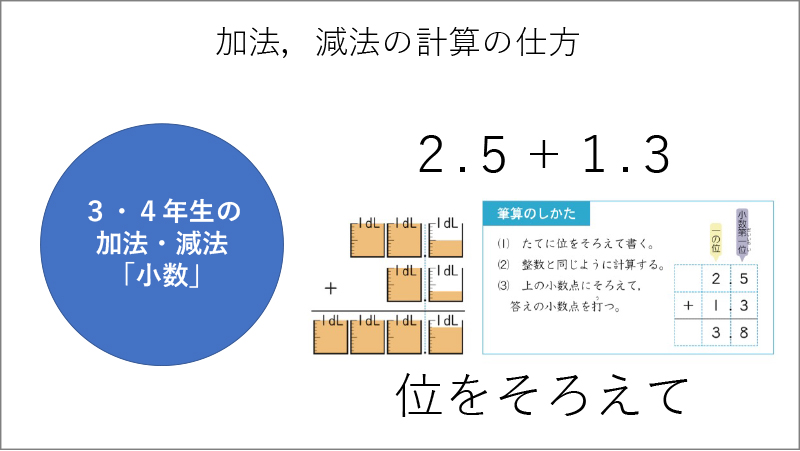
このように子供たちが、新しく得た視点でそれまでの学習を捉え直すことができれば、覚えるべきことはわずかで済みます。もし、このような統合がないまま１学年からの加法、減法の学習を個別バラバラにしていったとしましょう。そうすると、１学年では、10をつくることを学びます（資料１参照）。２学年では、ひっ算を学習し、同じ位同士で計算してまとめていきます（資料２参照）。３学年では、小数が出てきて位をそろえて計算することを学び（資料３参照）、４学年の同分母分数の学習では、分子だけを計算することを学び（資料４参照）、５学年では、通分して計算することを学びます（資料５参照）。

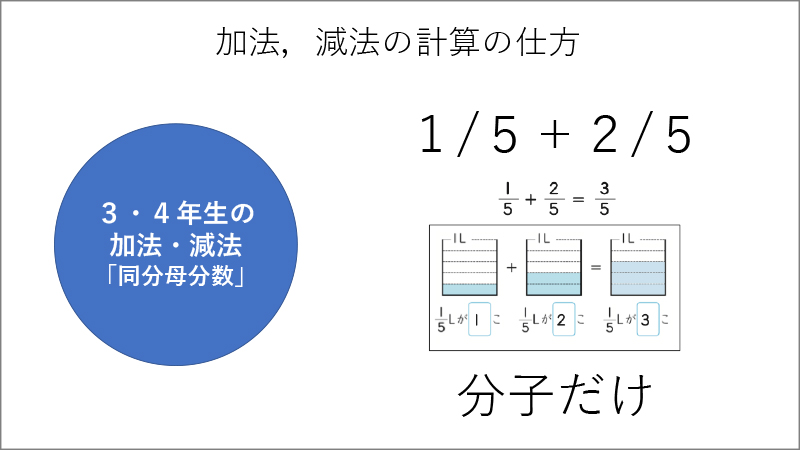
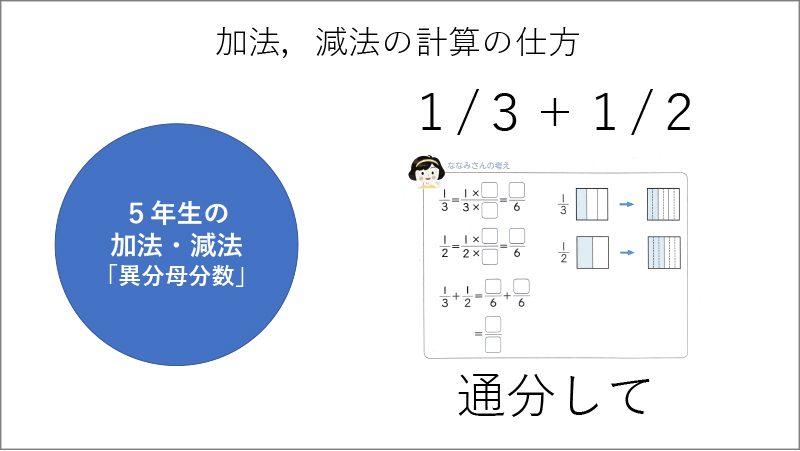
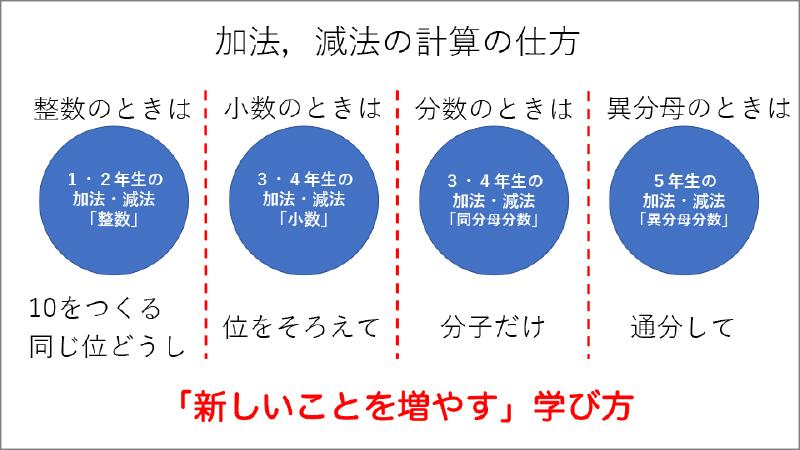
このように計算の方法（手続き）だけを学習すると、それぞれ別個のことを学ぶことになります。これは、子供たちが覚えるべきことをどんどん増やしていく学び方です（資料６参照）。もちろん、この後も学齢が上がるにつれて、どんどん増えていくことになります。そうではなく、先の子供のように通分の学習で単位を揃えるという視点を得たら、その視点で過去の学習をふり返って捉え直してみると、｢このときも、このときも、このときも同じ原理で、単位を揃えて計算していたんだ」ということに気付くわけです（資料７参照）。

算数では、このような原理原則に目を向けていくと学習し、覚えることが少なくなっていくのです。

割合は２年生のときからずっと学習してきている、ということを意識する

私はこの連載を行うと共に改めて、なぜ分数指導がむずかしいのかについて考えてきましたが、その過程で一つ確かにこれだと思う視点があったので、話をしておきたいと思います。

算数では分数の学習をする前にまず整数の学習をします。この整数の指導における大きな流れは、すべて量から入って割合に入っていきます。最初に３個とか３mという量から入り、抽象化された３という数から３倍という関係（割合）を表すものに入っていくわけです。それに対し、分数の学習は、もともと分数に対して子供がもっている感覚が割合なので、まず割合から導入されます。２学年の分割分数がまさにそうですが、〇〇の[MATH]\(\frac{1}{3}\)[/MATH]というような割合から入り、そこから[MATH]\(\frac{1}{3}\)[/MATH]mというような量に入っていくわけです（資料８参照）。

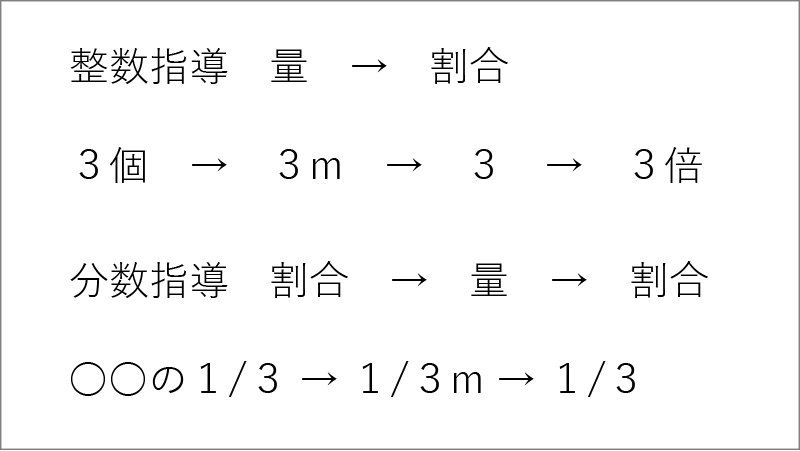
まさに整数とまったく真逆の展開をして割合から入っているために、｢２mを３等分すると…」と量を問われる問題でも、子供たちはなかなか割合から抜けられないのだと思います。もちろん、５学年の学習でまた割合に戻っていくのですが、最初に割合から入って量へと入っていく流れがあることが、子供にとってむずかしいのだと思います。

しかし、この連載で繰り返し説明してきた通り、すべては有理数の表現形式であり、整数や小数で表現できないときに分数を用いているということで、量の見方について学習するときにも、割合的な見方が根底にあれば、一貫した指導で混乱を招きにくくなるのではないでしょうか。ただ現実には、｢ここは量のことを学習するのだから」と、量のことにしか触れない授業実践も少なくありません。ですから、私は３学年、４学年ともに割合の見方に触れる指導を入れています（注：例えば、３学年で端数を扱う場合、少量の水を「ちょっと」と表現させ、それは「５等分したものの１つ分＝[MATH]\(\frac{1}{5}\)[/MATH]」と表現させる）。

子供たちは、５学年の学習で初めて割合や商を表す分数を学習するわけではなく、これまでの学習でも同様の経験をしており、割合という見方で見直すと…わり算の答えという見方で見直すと…分数を使えば、すっきり表現できるようになるということを学習するのが５学年です。つまり、割合という見方は２年生のときからずっと学習してきている、ということを意識し、系統立てて指導しておくと、５学年の分数の学習はハードルが上がるものではありません。むしろ、｢分数の表現を用いるとすっきり表せる」といった感じの学習になるだろうと思います。

さらに言えば、５学年の分数指導を考えるということは、２～４学年の分数指導をどう組織すればよいかを考えることになるのです。

※

ここまで５学年の内容と授業づくりでは、子供が間違えやすいところに重点を置いて授業づくりを紹介してきました。６学年の学習では、小数や分数の表現を統合する場面もあるので、５学年の内容ともつなげながら説明をしていきたいと思います。

執筆／教育ジャーナリスト・矢ノ浦勝之

つまずきなしの「分数」指導法
■異分母分数の加法を学習するよさは、たし算の原理原則を学ぶこと【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #8】
■わり算の商に分数を使えば、１つの数で表現できるという発見【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #7】
■子供の素朴な理解から生じた間違いに付き合う【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #6】
■子供たちが自ら数直線やテープ図をつくり、縦に見比べていくような学習を行う【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #5】
■単位分数を変えながら数直線づくりをし、分数も数であると意識させる【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #4】
■｢もとになるもの」については、しっかり意識付けをしていく【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #3】
■２年では、もとの大きさと部分の大きさを常に意識しながら指導 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #2】
■分数の５つの用い方を理解しておく 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #1】