小5算数「割合」指導アイデア《基準量の変化に着目し、比較量の求め方について筋道を立てて考える》
執筆/神奈川県横浜市立新鶴見小学校教諭・三塚大亮
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、神奈川県横浜市立伊勢山小学校副校長・黒木正人
目次
年間指導計画
・整数と小数
・体積
・合同な図形
・比例
・小数のかけ算
・平均
・単位量あたりの大きさ
・小数のわり算
・速さ
・図形の角
・整数の性質
・分数のたし算とひき算
・わり算と分数
・面積
・割合
・帯グラフと円グラフ
・円と正多角形
・□と△を使った式
単元の展開(各時の主な学習活動内容)
第1時 シュートの入った回数とシュートした回数の関係に着目し、一番よく成功した人の比べ方を考える。
第2時 シュートの入った回数とシュートした回数の関係に着目し、倍の意味を基にして、割合を用いた2つの数量の関係の比べ方について考える。
第3時 2つの数量の関係に着目し、百分率や歩合での表し方を考える。
第4時 基準量、比較量、割合の関係に着目し、基準量と割合から比較量を求める方法を考える。
第5時 基準量、比較量、割合の関係に着目し、比較量と割合から基準量を求める方法を考える。
第6時 割合の適用問題に取り組む。
第7時 和や差を含んだ割合の表現に着目し、基準量と割合から比較量を求める方法を考える。
第8時(本時)学習内容の生活への活用
第9時 学習内容の習熟・定着
本時のねらい
3つの店の割引の仕方を考えることを通して、基準量の変化に着目し、比較量の求め方について筋道を立てて考える。
評価規準
数直線や式を用いて、基準量の変化を説明し、根拠を明確に示すことができる。
本時の教材のポイント
ここでは、割引のさらに割引の問題場面を通して、基準量が変化していることを議論して学習を進めていきます。2回目の割引を考える場面では、基準量となる大きさに着目することが大切となってきます。何を基準量とし、何を比較量とするのかを気付けるようにします。その際に、図や式を用いて、1回目の基準量と2回目の基準量が変化していることを考察していきます。数直線に表すことで、基準量や比較量がどの数値なのかを筋道を立てて考え、乗法として考えられる根拠を明らかにして説明することができるようにします。
本時では、同じ商品が売られている3つのお店で、割引の方法がそれぞれ異なる場面を提示します。A店は定価の40%引き、B店は定価の20%引きのさらに20%引き、C店は定価の30%引きのさらに10%引きとします。そこで教師が、「定価1000円の文房具セットを買うとき、どのお店がいちばん安いですか」と問います。子供たちの議論を整理していくと、「基準量が変化するのではないか」という「問い」が生まれます。前時までの割引、割増の学習を通して、数直線を使って基準量や比較量の数量関係を明らかにし、説明することができるようになっています。その学習経験を基に、最初の基準量である1000円から割引した値段を求め、そこからさらに割引した値段を求めていきます。その際に、一度割引したことで基準量が変化していることに、子供たちが気付けるようにします。一度割引したことで、基準量が変化しているために、最終的な値段が異なってくることを、数直線を使って基準量と比較量の数量関係を、筋道を立てて説明することができるようにします。
最後に、ある商品で定価の50%引きのさらに50%引き、という場面を提示します。適用問題として扱い、基準量の変化に着目して割引後の値段が考えられていることを評価していきます。なお、授業の中では、基準量を「もとにする量」、比較量を「比べられる量」として進めます。
本時の展開
同じ文房具セットが定価1000円で売られています。A店、B店、C店の3つのお店で次のような売られ方がされています。
A店では、この1000円の商品が40%引きで売られています。別のB店では、1000円の20%引きで売られていました。B店では、レジで会計をする際に、割引した値段から、さらに20%引きするそうです。C店では、1000円の30%引き。さらにレジで会計する際に、割引した値段から10%引きします。
定価1000円の文房具セットを買うとき、どの店がいちばん安いですか。
A店は、前の学習した場面と同じですね。この店だったら、代金を求められそうです。
B店は、さらに……? 20%引きしたあとに、さらに20%引きにすると、どう考えたらいいのかな。
C店も、30%引きの10%引きは、もとの値段、つまりもとにする量はどうなるのだろう。
割引した後は、どれももとにする量が変わるということなのかな。
一度20%引いて、その20%割引した値段から、さらに20%引くということでしょ。
最初は定価1000円のところから20%引くから、もとにする量は1000でいいけれど、そこからさらに20%引くということは、その20%割引された値段がもとにする量になると思います。
もとにする量が1000ではなくなるということですか。
なるほど。割引したところから、さらに割引するということが、前回の学習と違いますね。
C店も同じように考えてみると、最初は定価の1000円のところから30%引きだから、もとにする量は1000でいいけれど、そこからさらに10%引きということは、その30%引きした値段がさっきのB店で、もとにする量とした20%引きの値段とは違います。
そうなると、考えることが明確になってきましたね。
※A店の割引後の値段の求め方は、前時の確認のために全体で取り組む。
それでは、A店で売られている文房具セットの代金はいくらになりますか。
40%引きの値段は、40%の値段を求めて、もとにする量から引いて求めました。
式は1000×0.4=400。これが、割引する40%の値段です。だから、もとにする量の定価1000円から400円を引いて、1000-400=600。この600円が、割引した後の代金となります。
1000がもとにする量と考えていいから、分かりやすいですね。
私は別の考え方で、100%の値段から40%の値段を引いた、60%の値段を求めました。
式は、1000×0.6=600。この600円が、割引後の代金となります。
今の説明で0.6が出てきましたが、これは何を表していますか。
100%から40%を引いた60%のことです。100%を割合で表すと1で、40%を割合で表すと0.4だから、1-0.4=0.6となります。
もとにする量が1で、比べられる量が0.6ということですね。
1つの式にすると、1000×(1-0.4)=1000×0.6=600です。
この場面も数直線で表すにはどうしたらいいですか。
まず、下の数直線に割合の1を書きます。1000がもとにする量なので、1の上の数直線の値が1000となります。40%引きなので1-0.4=0.6なので、求めたい割合の0.6を書き、その上の値段を□にします。
だから、1000×0.6の600円が、今回求める文房具セットの代金になります。
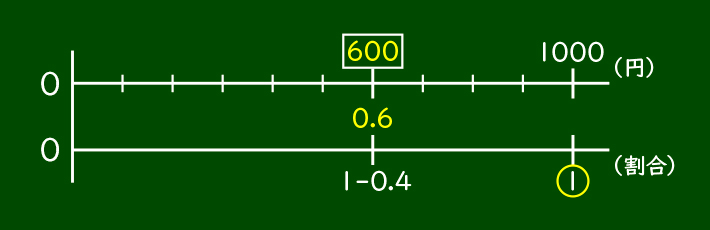
もとにする量が割引前の値段の1000円、比べられる量が割引した後の代金となることが確認できましたね。それでは、今回は割引した後の値段から、さらに割引する場合を考えていきましょう。
最初に割引したときは、A店と同じように、もとにする量は1000で考えるけれど、その後「さらに」割引するから、一度割引した値段をもとにする量にして考えないといけないですね。
もとにする量が変わることに注目しないといけないですね。
改めて、今日考えることが明確になったところで、B店とC店で買うときの代金を求めましょう。

数直線や式を用いて、もとにする量がどのように変わるのか考えよう。
見通し
最初に割引した値段を求めて、何がもとにする量なのかを考えよう。
最初に割引した値段をもとにする量にして、さらに割引する値段を求めよう。
数直線を用いて、もとにする量が変わる様子を、説明しよう。
自力解決の様子
A つまずいている子
・もとにする量(基準量)が分からず、教師の支援を待っている。
・もとにする量(基準量)が変わることを全体確認しているにも関わらず、基準量を変えずに求めようとしている。
B 素朴に解いている子
・立式することができ、それぞれのお店の割引後の代金を求められている。
・割引後の代金は求められているが、もとにする量(基準量)の変化を数直線に表すことが難しく、筋道を立てた説明をすることに困っている。
C ねらい通り解いている子
・最初の割引の後の値段をもとにする量(基準量)として、さらに割引した後の代金を求めることができている。
・もとにする量(基準量)が1回目と2回目では異なることを、数直線や式を用いて説明することができている。
全体発表とそれぞれの考えの関係付け
それではお互いの考えを伝えていきましょう。B店から考えますか。
まず、最初の割引は定価1000円の20%引きなので、1000×(1-0.2)=1000×0.8=800です。だから、最初の割引で800円になりました。
1-0.2の0.8は、20%を割合で表すと0.2で、もとにする量の1から0.2を引いて0.8となります。
私は、1000×0.2=200として、割引する値段を求めました。定価の1000円から200円を引いて、800円が最初の20%引きの値段になりました。
最初の20%引きの800円が、今度はもとにする量になります。「レジで会計する際に、割引した値段からさらに20%引きする」ということなので、1000がもとにする量ではおかしくなります。
そうすると、800円がもとにする量になって、その20%引きなので、800×(1-0.2)=640となり、代金は640円です。
「割引した値段からさらに割引する」から2回とも1000円がもとにする量なのはおかしいということですね。
みなさんで、意見をつなげて、考えが深まってきましたね。考えるときには何に気を付けたらいいですか。
割引した値段からさらにと考えるので、20%引きした値段を1と考えることが大事だと思います。
定価の1000円がもとにする量ではなくて、割引した800円がもとにする量になります。
「さらに」となると、もとにする量が変わってくるということです。
とてもいいところに目を付けていますね。一度目の割引と二度目の割引とでは、もとにする量が変わるということですね。
今の説明を、数直線で説明します。
まず、下の数直線に割合の1を書きます。1000がもとにする量になるので、1の上の数直線の値が1000となります。20%引きなので、先ほど説明があったように、1-0.2をして0.8を計算します。ここで求めたい割合の0.8を書いて、その上の値段を□にします。
1000×(1-0.8)=800をして求められた800が、二度目の割引のときにはもとにする量になるので、もう1つ別の数直線をかきます。同じように下の数直線に割合の1を書きます。今度は800がもとにする量になるので、1の上の数直線の値が800となります。20%引きなので1-0.2=0.8をして、求めたい割合の0.8を書き、その上の値段を□にします。
だから、800×0.8の640円が、文房具セットの代金になります。
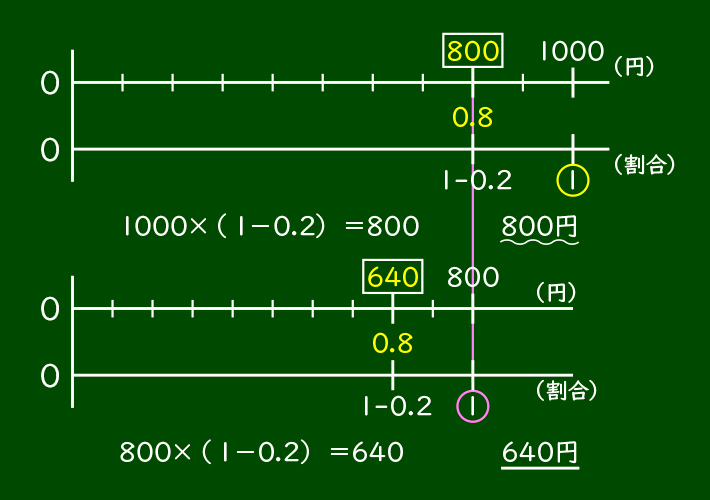
そうすると、A店のほうがB店よりも安いということになります。
もとにする量が変わると、40円も変わってしまいました。
C店も同じように考えられますか。
まず、最初の割引は定価1000円の30%引きなので、B店と同じように考えて、1000×(1-0.3)=1000×0.7=700です。だから、最初の割引で700円になりました。
700円が、今度はもとにする量になります。そうすると、700円の10%引きということになるので、700×(1-0.1)=630となって、代金は630円となります。
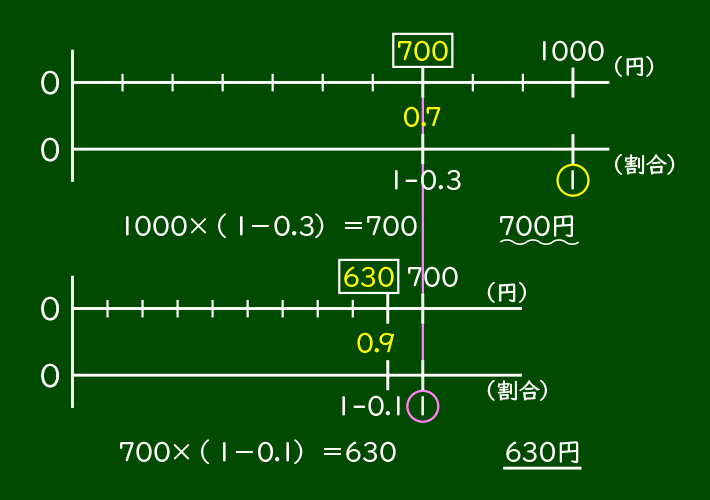
今度はB店よりもC店のほうが10円だけ安くなりました。
やっぱり、二度目の割引のときは、1000をもとにする量にしてはダメですね。
割引したところから、さらに割引すると、もとにする量が変わるから、最終的に求める比べられる量も変わってくることが分かりました。
前回の学習と、今回の学習の違いは、もとにする量が変わるということでしたね。
家の人と一緒にスーパーでお買い物するときに使えそうです。
「さらに」になると、もとにする量が変わると比べられる量の代金も変わるから気を付けて計算したいです。
それでは最後に、次のような場面の代金を求めてみましょう。
評価問題
スーパーで、220円のお肉が50%引きで売られています。わり引きしたねだんから、会計の際にさらに50%引きになります。代金はいくらになりますか。

子供に期待する解答の具体例
【式】220×(1-0.5)=110
110×(1-0.5)=55
【答え】55円
まとめ
構成/桧貝卓哉 イラスト/横井智美・やひろきよみ 図版作成/永井俊彦

