小学算数「構造的板書」の工夫とコツ（小数／体積）

スッキリした分かりやすい構成で、子どもたちに伝わりやすい板書の書き方を指南する本シリーズ。今回は、算数の「小数」と「体積」がテーマです。 構造的板書を長年研究している樋口万太郎先生（京都教育大学附属桃山小学校教諭）に、板書で気をつけるべき「配置」のテクニックを中心に教えていただきます。

板書スキル１：大切なことは真ん中に書く

★小数

算数の板書というと、左上から始まり右下へと書いていくというのが、あたりまえのようになっています。しかし、黒板を三分割したときに、子供たちの視線が集まるのはどこでしょうか。それは間違いなくど真ん中の部分です。だから、そこにその授業において大切なことを書くようにするのです。

では、算数の授業において大切なこととはなんでしょうか。それは、考え方やまとめです。下の板書では、真ん中にまずじゃけんゲームのルールを書きました。通常であれば、ルールの部分が問題文になります。問題文が真ん中にあれば、1時間の授業を終えた後、振り返りがしやすくなります。今回の板書では「めあて」を書いていませんが、もし書くのならやはり真ん中に書きます。

本時は、10 倍、100倍、1000倍することで小数点がどのように移動するのか、位がどうなるのかを理解することをねらいとしています。そのためにじゃんけんゲームを行います。ゲームはとても盛り上がりますが、活動あって学びなしの状態になりやすいです。そうならないためには、ねらいがあることが大切です。

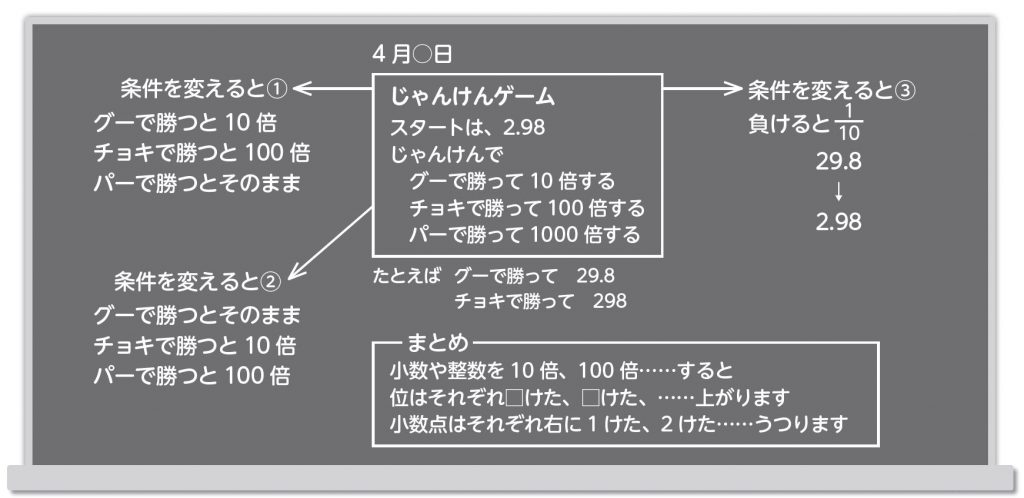
ルールを書いても、そのルールを全員がすぐに理解できるとは限りません。そこで、例として行なった結果をルールの下に書くことでルールの理解度が増します。このとき、子供たちはじゃんけんゲームの結果をノートに書くように言っておくことで、本時のねらいを達成しやすくなります。

同じルールでゲームをしていては、子供たちは飽きてしまいます。そこで子供とルールの変更を考えるのです。それを左右の場所に書きます。条件を変える③では、最初のルールに負けると10 分の1というルールを加えます。子供たちの実態に応じて、100分の1や1000分の1を入れてもいいことでしょう。

子供たちは活動を通して、小数点がどのように移動するのか、位がどうなるのかに気づいていることでしょう。そこで、上の板書のように空欄部分をつくり、まとめを書き、空欄部分は子供たちに埋めさせるようにします。もちろんまとめは大切なものなので、真ん中に書きます。

まとめは、あらかじめ用意していた紙を貼るのではなく、その場で書くようにしましょう。なぜなら、できる限り、子供たちから出てきた言葉で表現したいからです。

板書スキル２：問題、式、考えをつなぐ

★体積

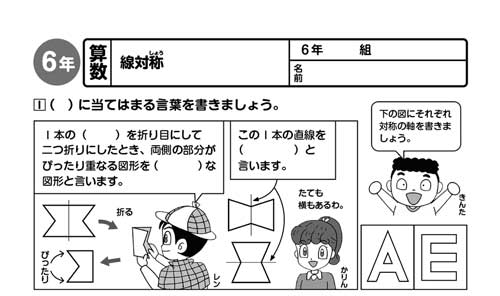
算数は、（　　）と（　　）をつなぐ教科です。と言われたとき、（　　）には何が入ると思いますか。

• 問題と図
• 図と式
• 問題と式
• これまでの考えと新たに学習する考え
• 自分の考えと他者の考え

などたくさんあげることができます。それぞれをつなぐために使うのが、線や矢印、○や□ で囲んだりするといったツールです。つなぐことで、理解や考えを深めたりすることができます。

次の板書は、単元「体積」の2時間目の板書です。1時間目に活動を通して、体積とは1㎤の立方体の何個分かということを理解しています。そのことを活用し、2時間目では直方体と立方体の体積について考え、公式を導いていくことをねらいとしています。これらの学習の流れは、四年生の面積の学習と同じであるため、子供たちはスムーズに取り組むことができるでしょう。

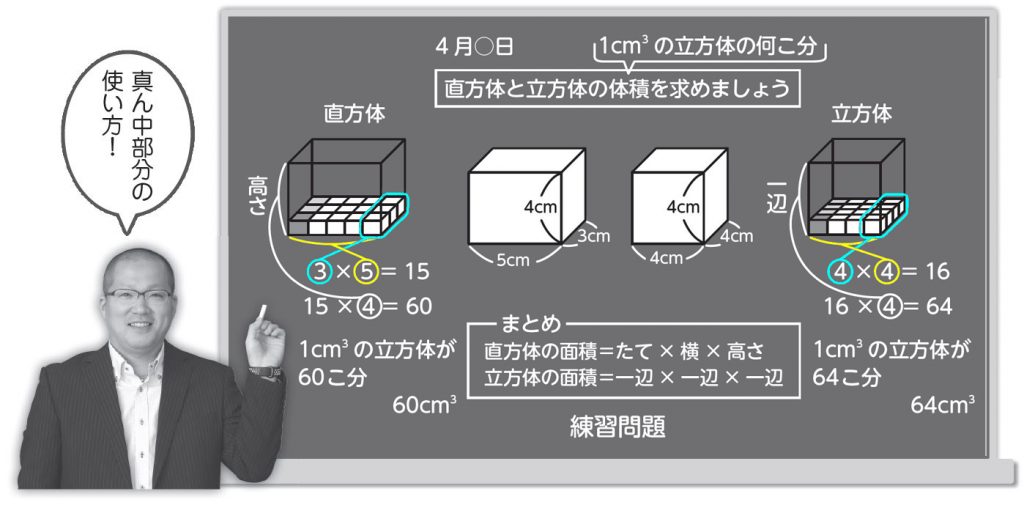
この授業でも スキル1 ：板書の配置 を使用し、まずは真ん中に問題を書き、教科書の問題を拡大コピーしたものを貼ります。そして、体積とはなんだったのかを振り返らせ、そのことをふきだしで書いておきます。（ふきだしも構造的板書では必要不可欠のものです）。

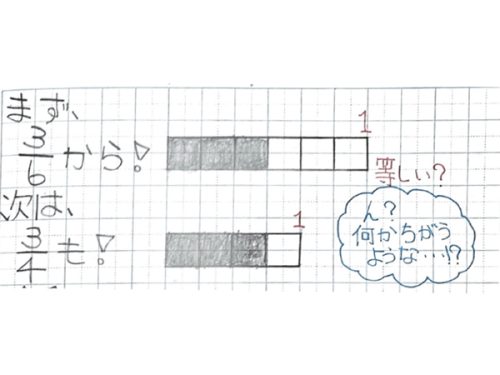
そして、左部分で直方体のたてに1㎤の立方体が何個分あるのか、横に1㎤の立方体が何個分あるのか、高さにあたる部分に1㎤の立方体が何個分あるのかということを考えさせます。

そのときにただ、3×5と式を書くのではなく、3はどこを示しているのか、5はどこを示しているのかを図と式を線や○でつなげることで、より式の意味が分かり、式について理解しやすくなります。右部分で立方体のときにも同様のことを行います。

先行学習の子たちは、直方体と立方体の体積の公式を理解しているでしょう、しかし、その意味が分かっているかには疑問がつきます。こうすることでどの子も理解できるようになります。数と計算領域の学習で、問題文と式をつなげることも有効です。

その上でまとめとして、それぞれの公式についてまとめ、練習問題を行います。練習問題を真ん中に書いたのは、すぐ上にある公式を活用し、求めることができるようにするためです。

『小五教育技術』2018年４月号より