小３算数「三角形と角」指導アイデア《三角形の角の大きさの相等・大小関係》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.03.16

単元の展開

第１時　辺の長さに着目した三角形の弁別
▼
第２時　二等辺三角形の作図
▼
第３時　正三角形の作図
▼
第４時　円の性質に着目した二等辺三角形と正三角形の作図
▼
第５時（本時）三角形の角の大きさの相等・大小関係
▼
第６時　二等辺三角形と正三角形の角の特徴
▼
第７時　まとめ

本時のねらい

角の意味や角の大きさの相等や大小を理解し、調べる。

評価規準

角の大きさの相等や大小について、直接比較や間接比較を行い、説明することができる。

本時の展開

前時までに、辺の長さに着目して三角形を調べてきましたね。今日は三角形のかどの形について調べていきましょう。この三角形です。

わあ、三角定規だ。

そうですね。角の形を調べていきますが、算数では角の点を「ちょう点｣、頂点から出ている２つの辺がつくる形を「角｣、また角をつくっている辺の開き具合を「角の大きさ」と言います。

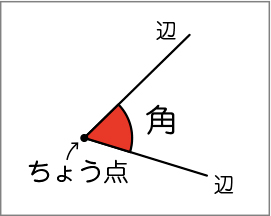
三角定規の角について調べましょう。

三角定ぎの角を調べましょう。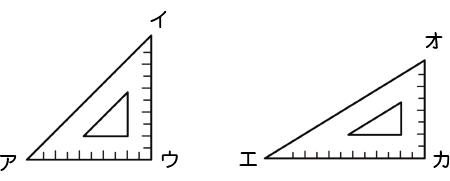

ウとカは直角になっています。

エはとがっています。

アとイの角の大きさは同じかな。

他の角の大きさはどうかな。

見た目では比べられないものもあるね。

それでは、三角定規の角の大きさを調べましょう。

２枚の三角定規の角の大きさの比べ方を考えよう。

見通し

どのように比べたらいいのかな。

長さ比べや重さ比べのときにやったように比べられないかなあ。

それでは、自分なりの方法でやってみましょう。

三角定規の角を重ねて比べてみよう。

三角定規を紙に写して、それを重ねて比べてみよう。

三角定規の角だけ紙に写して、重ねたり切ったりして比べてみよう。

自力解決の様子

A　つまずいている子
・イとオは三角定規を重ねて比べられるが、アとイは同じ三角定規なので重ねることができないため、途中で解決が止まってしまう。

Ｂ　素朴に解いている子
・アとイの角の大きさを自分の三角定規だけでは比べられないので、友達の三角定規を借りてアとイを重ねてみたら同じになった。
・紙に写したアと三角定規のイと比べて同じであることが分かる。

Ｃ　ねらい通り解いている子
・三角定規を２枚とも紙に書き写して、アとイやエとオを比べる。
・紙に写した三角定規の形を折って、アとイを合わせるとぴったり重なることから、同じであることが分かる。
・すべての角だけ紙に写して、それぞれを重ねると、角の大きい順が分かることに気付いている。

学び合いの計画　

ここでは、長さや重さの比較の際に学習した量の比べ方を基に学習を進めていきます。直接比較では、三角定規同士を重ねたときに、直角二等辺三角形と直角三角形の２つの三角定規を重ねると、角の大きさを比べることはできることに気付かせます。しかし、それぞれの同じ三角定規の角ア、角イ、角ウや、角エ、角オ、角カは直接重ねることができないことを押さえます。

直接比較の限界を明らかにした後、三角定規の形を紙に写し取り、角の大きさを比較できる間接比較をすることにより、写し取った紙を折ったり重ねたりして、それぞれの角の大きさを比べることができることを確認します。さらに、「すべての角の大きさを同時に比べるにはどうしたらよいでしょうか」と教師が問い、写し取った６個の角を切り取り重ねることにより、手際よく明確に角の大きさや大きさの順序が分かることを明らかにします。

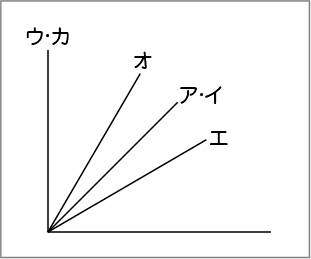
直接比較と間接比較の検討をしたのち、｢エの角を基にすると、他の角はエの角の大きさのいくつ分と言えるでしょうか」と教師が問うことで、角の大きさをある単位を基にして捉え直すことに気付いていくようにします。そうして「オはエの２つ分です」など、任意単位による数値化した測定の素地となるとともに、三角定規をいくつか組み合わせて「エを３つ合わせるとウになる」など、友達との協働的な学びが生まれます。