小６算数「比例と反比例」指導アイデア《クリップの数とクリップの重さとの関係》
執筆／富山県高岡市立木津小学校教諭・屋鋪善祐
監修／文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一
目次
単元の展開
第１時 伴って変わる２つの数量の変わり方について考える。
▼
第２時（本時）クリップの数とクリップの重さとの関係を調べ、説明する。
▼
第３時 針金の長さと重さの２つの数量が伴って変わることを調べ、比例の意味について考える。
▼
第４時 比例の性質について考え、比例の関係は式で表すことができることを知る。
▼
第５時 比例の性質を利用して、比例の関係を式で表す。
▼
第６時 ｘとｙの関係を式に表し、決まった数は何を表しているか考える。
▼
第７時 比例の関係をグラフに表すことを考え、かき方と特徴を知る。
▼
第８時 グラフを見て、比例しているかどうかを判断したり、数値を読んだりする。
▼
第９・10時 比例の関係を表す式やグラフを用いて、問題解決の方法を考える。
▼ 《比例の式やグラフを用いて、問題解決の方法を考える》
第11時 反比例する二つの量の変わり方を調べ、反比例の特徴を考える。
▼ 《反比例する二つの量の変わり方と特徴》
第12時 反比例の性質を見付け、反比例を表す式やグラフについて考える。
▼
第13時 反比例の性質を利用して、問題解決の方法を考える。
▼
第14・15時 適用問題を解く。
本時のねらい
伴って変わる２つの数量の関係を活用し、それらの変化や対応の特徴を生かして、表や式を用いながら問題の解決の方法を考える。
評価規準
伴って変わる２つの数量を見いだして、それらの関係に着目し、変化や対応の特徴を生かして問題の解決について考えている。（思考・判断・表現）
本時の展開
クリップは、全部でだいたい何個あるでしょう。
あるものを見せますよ。
※たくさんのクリップを提示する。
わぁ！ すごいたくさんあるよ！ 何個くらいあるのかな。
ここにたくさんのクリップがあります。全部でだいたい何個あるでしょう。
100個……、いやもっと。500個くらいかな。
1000個以上ありそう！
全部でだいたい何個あるのか、どのように考えればいいですか。
１個ずつ数えればいいです。
大変！ 時間がとてもかかりそうだよ。
だいたいの数でよいのなら、クリップの重さを量ったらどうかな。
どうしてクリップの重さを量るといいと思ったのですか。
クリップ１個の重さを量って、全部の重さをクリップ１個の重さで割るとクリップの数が分かると思います。
○○さんの考えについて、みなさんはどう思いますか。
解決できそうな考えだと思います。
クリップの数が多くなればなるほど、クリップの重さも重くなるはずだから、○○さんの考えでクリップの数を求めることができると思います。
○○さんの考えは、これまでに学んできた比例の考えを使っていると思います。
何と何が比例の関係だと言えるのですか。
クリップの「個数」と「重さ」です。
クリップの「個数」と「重さ」が比例の関係と言えるのはどうしてですか。
クリップの重さはどれも同じです。だから、クリップの数が２倍、３倍……となれば、クリップの重さも２倍、３倍……となるはずです。
他のみなさんも、クリップの「個数」と「重さ」が比例の関係にあると思いますか。
私も比例の関係になっていると思います。
比例の関係を使って考えていくために、まず何を知りたいですか。
クリップ１個の重さです。
測ってみよう！
※クリップ１個の重さを測定する。
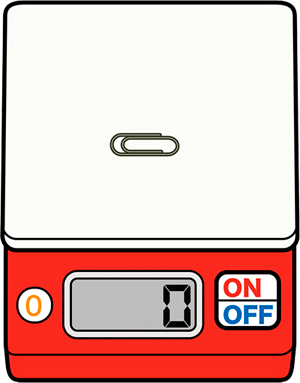
あれ、「０ｇ」だよ。おかしいな。
きっと、軽すぎて量れないんだよ。
１個の重さが１ｇより軽いから、数としては出てこないんだよ。
困りましたね。どうしたらよいですか。
クリップの数を多くして、はかりに載せてみたらいいと思います。
そうは言っても、７個や９個だと１個あたりを求める計算に手間がかかります。10個にしてみたらどうかな。
じゃあ、クリップ10個の重さを量ってみよう。
※クリップ10個の重さを測定する。
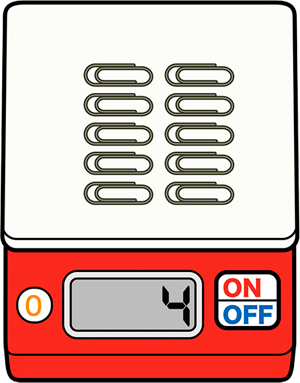
10個だと４ｇでした。
10個が４gということは、１個は0.4ｇなんだね。
だいたい0.4ｇと言ってもいいかも知れないけれど、まだまだ端数があるかも知れないね。
そうだけど、みんなで考えていくのは、１個0.4ｇでもいいと思います。
僕は、できるだけきっちりとした数を出したいので、100個の重さも量ってみたいです。
クリップ１個の重さを0.4ｇで考えていこうという思いと、できるだけ正確にきっちりと調べたいという思いの２つがあるみたいですね。どうしたらよいでしょうか。
どれだけ厳密に調べていっても、クリップ１つ１つの重さには誤差があるはずです。どのクリップも完全に同じ重さということはないので、ある程度の正確さまで求めたら、その数を使っていけばいいと思います。
僕は考えたり計算したりするのが大変だから、10個４gで調べていきたいです。
いくら正確にしたいからといっても、調べる個数をあんまり多くしたら、個数を全部数えていったほうがいいということになってしまいます。
計算で求めるよさを考えると、10個４gが手頃なのではないかと思います。
くわしく量りたい人は、100個の重さも量ってみてもいいと思います。その後で、どちらの方法を取るか決めたらいいのではないですか。
みんなの話合いで解決の方向が見えてきたようですね。それでは、学級全体としては、10個４gを使って調べていくことにしましょう。○○さんのようにできるだけくわしく調べたい人は、100個の重さを量って、そこからより正確な個数を出してみて、みんなの考えを補っていってくださいね。
あとは、クリップ全部の重さが分かればいいです！
それでは、クリップ全部の重さを量ってみましょう。
※クリップ全部の重さを測定する。
クリップ全部の重さは280ｇだね。
クリップ全部の重さが280ｇということが分かって、クリップの数が全部でだいたい何個あるのかを計算で求めることができそうですか。
できそうです。
できそうですが、ただ数を求めるということよりも、どんな考えで求めるかが大事だと思います。
どんな考えを使おうと思っているのですか。
クリップの「個数」と「重さ」は比例しているので、それを使おうと思います。
クリップ１個分の重さが0.4ｇだから、｢0.4×□＝280」で考えていこうと思います。
僕は10個で４ｇを使って考えていこうと思います。比を使った考えです。
それでは、クリップの「個数」と「重さ」が比例の関係にあることを使って、クリップ全部の個数の求め方を考えていきましょう。
｢個数」と｢重さ」が比例の関係にあることを使って、全部の個数の求め方を考えよう。
見通し
クリップの「個数」と「重さ」の比例関係を使えば求められそうだよ。（方法の見通し）
全体の重さ280ｇを１個の重さ0.4ｇで割れば全体の個数を求めることができそうだ。（方法の見通し）
クリップの「個数」と「重さ」の比を考えても求められそうだ。（方法の見通し）
10個で４ｇなのだから、1000個なら400ｇになる。クリップの数は、1000個よりは少ないはずだ。（結果の見通しなど）
自力解決の様子
A つまずいている子
比例の性質を活用して求めていくことに十分な納得ができていない。
・クリップの数が多くなればなるほど重くなるというイメージはもっている。
・「クリップ１つ分の重さ×個数＝全体の重さ」というかけ算の関係は理解しているが、クリップ１つ分の重さが小数の0.4ｇになるので、その計算にとまどっている。
Ｂ 素朴に解いている子
重さと個数が比例の関係にあることを感覚的に捉えている。
・クリップの数が２倍・３倍・４倍……になれば、その重さも２倍・３倍・４倍……になることの理解とイメージをもっている。
〈１個の重さを基に考えている〉
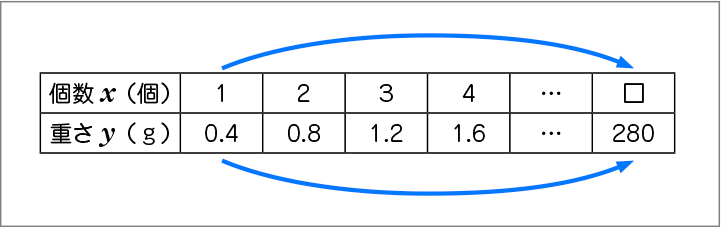
全体の重さ280ｇを１個の重さ0.4ｇで割ればよい。
0.4×□＝280 □＝280÷0.4＝700
＜10個の重さを基に考えている＞
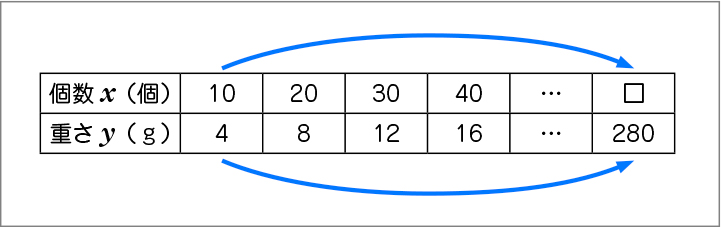
全体の重さ280ｇを10個の重さ４ｇで割って、その数を10倍すればよい。
４×■＝280 ■＝280÷４＝70 □＝70×10＝700
Ｃ ねらい通り解いている子
重さは個数に比例すると考え、比例の表の中から必要な比を見付け出して、多面的に考えている。
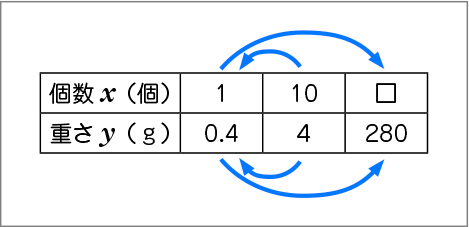
４÷10＝0.4
280÷0.4＝□
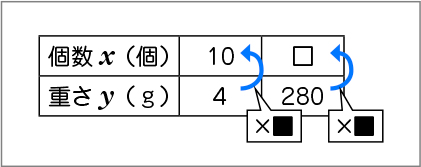
４×■＝10
■＝10÷４＝2.5
280×2.5＝□
10：４＝□：280
学び合いの計画
｢クリップ」を題材として、全部の個数を求めることを投げかけます。多数のクリップを目の前にした子供たちは、数えることの大変さを感じ、既習内容を基に解決できないか主体的に考えようとします。そのなかで、クリップの「個数」と「重さ」の関係に着目し、日常生活の場面で比例関係を活用して問題解決を行っていきます。
大切にしていきたいことが２つあります。１つ目は、伴って変わる２つの数量「個数」｢重さ」を見いだし、クリップの何と何が比例関係になっているのか理解することです。｢個数」と「重さ」の関係に着目すればよさそうだと、解決の見通しをもてるようにすることで、一人一人が自信をもって考えをつくり上げていくことができるようにします。
２つ目は、表や式を関連付けながら考えたり、話し合ったりできるようにすることです。つまずいている子は、比例関係をどのように活用すればよいか、それをどのような計算にすればよいのかをつかみきれていない場合が多くあります。そこで、問題の場面を表に表現し、どこに着目すればよいのか、その数量にどんな関係があるのか、それをどのように表や式、言葉を用いて表すのかなどを、ていねいに説明し合うことで、比例関係の変化や対応の特徴を捉えることができるように促していきます。
その際、１人の説明で終わるのではなく、｢○○さんの考えは伝わりましたか？」｢隣の友達に説明してみよう」など、ペアでの学習の場や友達の考えをなぞって考えてみる場を設けることで、考えを深めていくことができるようにします。子供たちがどこでつまずいているのか、どこに苦手意識を感じているのかなどを把握しながら、一人一人に応じた効果的な支援を大切にしていきましょう。
【参考】
実際に子供たちにたくさんのゼムクリップを持たせて測定する場合は、できるだけ大きな規格のものを用いるようにしましょう。実際に測定する場合の誤差を小さく抑えることができ、子供たちがゼムクリップを数える場合の操作がしやすくなります。ゼムクリップの他の素材として、釘やネジ釘などが用いられることがありますが、尖った部分のないもののほうが望ましいので、ボルトなどが望ましいでしょう。また、端数に強いこだわりをもつ子が想定される場合は、一円玉を用いることも有効です。一円玉１枚はちょうど１gです。
ノート例
Ａ つまずいている子
Ｂ 素朴に解いている子
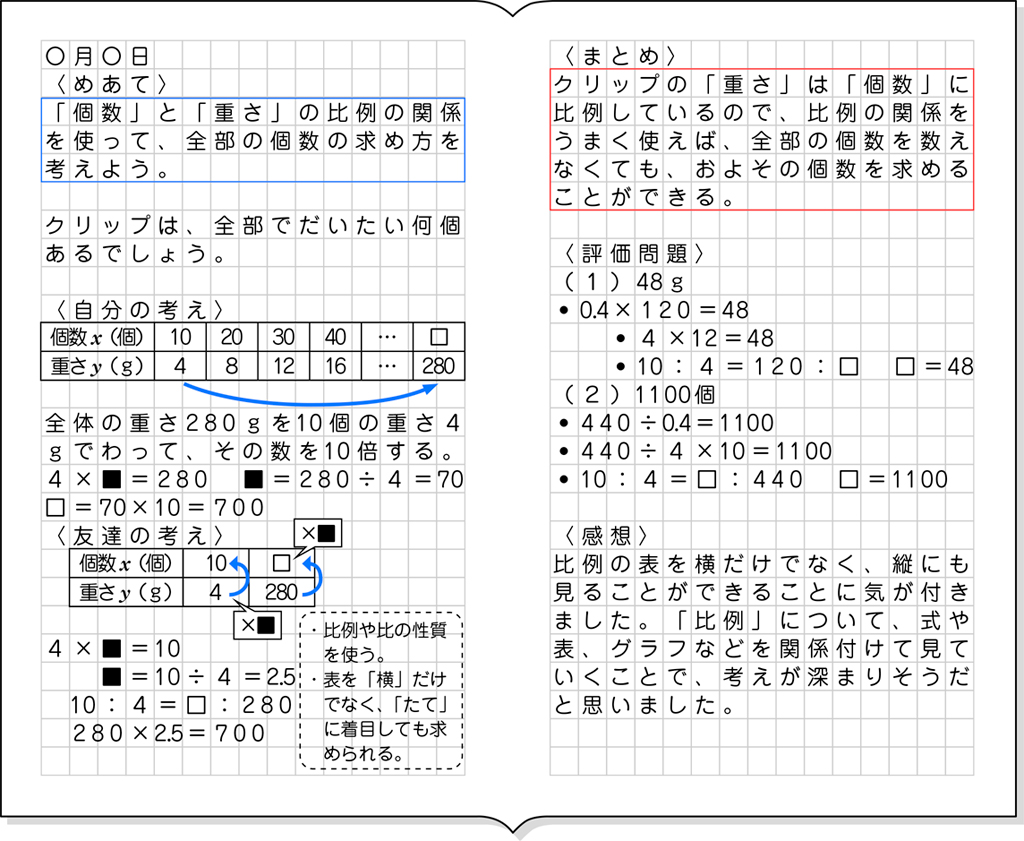
全体発表とそれぞれの考えの関連付け
どのようにして求めましたか。
〈○○さん〉僕は、さっき調べたことを表にまとめてみました。全体の重さ280ｇを１個の重さ0.4ｇで割ればよいので、0.4×□＝280、□＝280÷0.4＝700で求められます。
僕も同じ考え方だよ。
○○さんは、クリップ何個の重さを基に考えていますか。
｢クリップ１個の重さ」です。
クリップの数が２倍・３倍・４倍……になれば、その重さも２倍・３倍・４倍……になるから求められました。
本当だ。比例の性質を使えば求められます。
〈□□さん〉私は、○○さんと少し違って、｢クリップ10個の重さ」を基にして考えました。全体の重さを280ｇを１個の重さ４ｇで割って、その数を10倍すればよいので４×■＝280、■＝280÷４＝70、□＝70×10＝700で求められます。
○○さんと□□さんの考えを比べて、どのように思いましたか。
○○さんも□□さんも比例の性質を使って求めています。違うのは、基にしている数です。
比例の性質を使えば求められるんだね。
〈△△さん〉私も、表を使って求めたけれど、○○さんや□□さんと見方が違います。
え、どういうこと。
△△さんは、どんな考え方なのか分かりますか。近くの友達に説明してみましょう。
※相談タイム
△△さんは、どんな考え方なのか分かりましたか。
はい。重さは個数に比例すると考え、比例の表の中から必要な比を見付け出して求めています。
４÷10=0.4 280÷0.4＝700
必要な比を見付け出せば、簡単に求めることができるね。
３人の考えの共通点に気づきました。○○さんも□□さんも△△さんも、表を「横」に見て解決しています。
〈☆☆さん〉本当だ。だったら、表を「縦」に見ても解決できるのではないかな。
表を「縦」に見るとはどういうことですか。みなさん、分かりましたか。
どういうことだろう。
表を「縦」に見るとはどういうことなのか、近くの友達と相談してみましょう。
※相談タイム
☆☆さんの言いたいことは、分かりましたか。
はい。表を縦に見るとは、このように対応の特徴に着目して解決することだと思います。４×■＝10、■＝10÷４＝2.5、280×2.5＝□とすると、求めることができます。
つまり、表を縦や横に見て、比例関係を使えば求めることができるんだね。
あと、｢個数」と「重さ」の比に着目すると、10：４＝□：280と表せるので、比の性質を使っても求めることができます。
これまで学習してきた比は、比例とつながっているんだね。
では、本当にクリップが700個あるのか、みんなで数えて確かめてみましょう。
※全員で数える。
704個だったよ！ 僕たちが計算で求めたように、だいたい700個だったね。
どこまでくわしい数字を求めるかによるけど、だいたいでいいなら、いちいち数えるのではなく、比例関係を使えば計算で簡単に求めることができるんだね。
クリップ以外でも、いろいろな場面で比例関係を使えば、簡単に数を求められて便利そうだな。
学習のまとめ
クリップの「重さ」は「個数」に比例しているので、比例の関係をうまく使えば、全部の個数を数えなくても、およその個数を求めることができる。
比例をうまく使うと、問題の解決が楽になる。
比例について、もっとくわしく調べていきたい！
［これから学んでいくめあて］比例について、くわしく調べていこう。
評価問題
⑴ 同じクリップが、120個あります。クリップ全部の重さは、何ｇですか。
⑵ 同じクリップが、全部で440ｇあります。クリップは全部で何個ありますか。
子供に期待する解答の具体例
⑴ 48ｇ
・0.4×120＝48
・４×12＝48
・10：４＝120：□ □＝48
⑵ 1100個
・440÷0.4＝1100
・440÷４×10＝1100
・10：４＝□：440 □＝1100
本時の評価規準を達成した子供の具体の姿
伴って変わる２つの数量を見いだして、それらの関係に着目し、変化や対応の特徴を生かして問題の解決について考えている。
感想例
- 比例の関係を使えば、簡単に問題を解決できることが分かりました。
- １つしか求め方がないと思っていたけれど、友達の考えを聞いて、比例の関係を使った考え方がいろいろあることに気づきました。
- 比例の表を横だけでなく、縦にも見ることができることに気が付きました。
- クリップの「重さ」と「個数」の比例関係を使うことで、全部の個数を数えなくても、およその個数を求めることができるので、よりよい考えだなと思いました。
- これからも、比例の関係をうまく使って問題を解決していきたいと思います。そのために、比例についてもっとくわしく学んでいきたいです。
- 「かけ算」の見方、｢比」の見方、「比例」の見方は、つながっているんだなと思いました。「比」の見方と「分数」の見方と深い関係があるので、｢分数」の見方ともつながっていると思いました。
- 「比例」について、式や表、グラフなどを関係付けて見ていくことで、考えが深まりそうだと思いました。
ワークシートと板書例
イラスト／横井智美
