小６算数「資料の調べ方」指導アイデア《代表を選ぶ問題の解決について、データを分析して考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.09.13

単元の展開

第１時　２つの資料を比べ、それぞれの資料から平均値や最大・最小値を調べる。
▼
第２時　資料をドットプロットに表し、最頻値と中央値という代表値を理解する。
▼　
第３時　２つの資料のドットプロットの散らばりの様子や、代表値を調べて比べる。
▼　　　《ドットプロットの散らばりや代表値によるデータ評価》
第４時　資料を度数分布表に表し、散らばりの特徴を調べる。
▼
第５時　度数分布表を基に柱状グラフをかき、散らばりの特徴を調べる。
▼　　　《柱状グラフの散らばりの特徴》
第６時（本時）代表を選ぶという問題の解決について、データを分析して考える。
▼
第７時　様々なグラフの表し方を知り、その特徴や読み方を理解する。

本時のねらい

データの特徴や傾向に着目し、自分なりの根拠をもち、代表値を決め、問題の結論を判断する。

評価規準

データの特徴や傾向に着目して代表値を決め、問題に対する結論を判断しようとしている。（思考･判断･表現）

本時の展開

学校で「クラス対抗スポーツ大会」が行われることになりました。｢ソフトボール投げの部」は３日後です。そこで、クラスの代表者１名をＡ、Ｂ、Ｃさんのなかから決めます。３人のなかの誰を代表者にするとよいか、次の表を基にして考えましょう。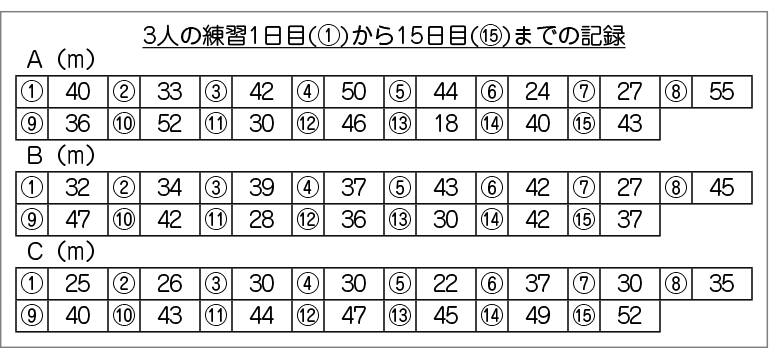

＜資料＞

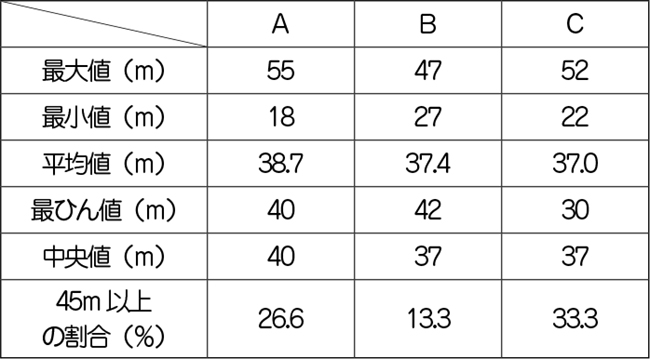
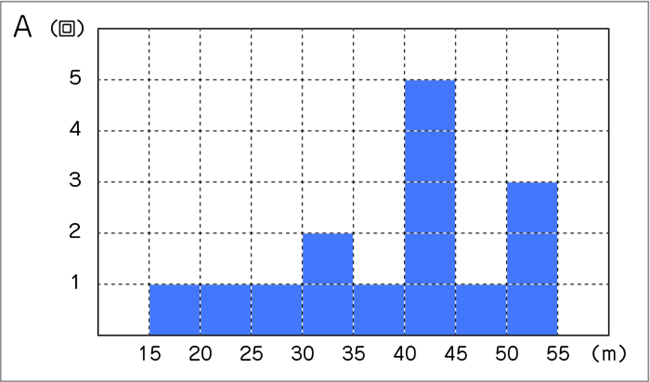
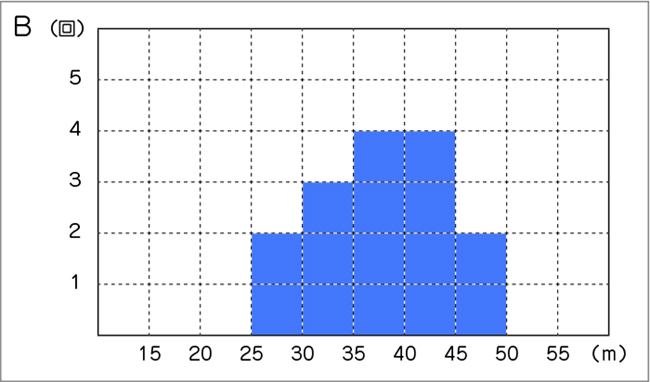
Ａ、Ｂ、Ｃさんのなかから、代表者１名を決めましょう。誰に決めればよいでしょう。

私は、平均値が一番高いＡさんがいいと思います。平均的に遠く投げているのだから間違いないです。

僕は、最小値が一番大きいＢさんがいいと思います。思うように投げられなくても、遠くまで飛んでいるほうが代表を任せられます。

２人の気持ちは分かるのだけど、そんなに簡単に決めてしまってもいいのかな。

優れた数値にだけ注目することに、疑問を感じているのですね。資料をもっとくわしく分析して、代表者を決める必要がありそうですね。誰を代表にすればよいと考えるのか、それは資料のどこから言えるのかについて、自分の考えをまとめてましょう。

誰をクラスの代表にすればよいか、資料を基に考えよう。

見通し

ドットプロットやヒストグラムを見ると、Ａさんたちの飛距離の安定感が分かりそうだ。（方法の見通し）

調子の悪い日もあったと思うから、一番悪い結果を除いて平均値を求めると、Ａさんたちのより正確な力が分かりそうだ。（方法の見通し）

毎回の結果を折れ線グラフに表すと、Ａさんたちの技能がどれだけ高くなってきたのか分かりそうだ。（方法の見通し）

注目した数値によって、代表にするとよい人が変わるなぁ。代表値を選ぶためのしっかりとした理由が必要だな。（結果の見通し）

自力解決の様子

A　つまずいている子
数が多すぎるので、どの数値に注目すればよいか分からなくて困っている。

Ｂ　素朴に解いている子
数値に注目して代表値を選んでいるが、大きい数値に影響され、くわしい分析ができていない。

Ｃ　ねらい通り解いている子
資料の数値だけでなく、他の数値から大きく離れた数値を外れ値として扱い、外れ値を抜いた平均値で比べたり、練習の後半部分の数値に目を付け、投げる技術の習熟度や練習の効果に注目したりして代表値を決めている。

学び合いの計画

本時までにドットプロット、ヒストグラムなどのデータの整理の仕方や、平均値、最頻値などのデータの特徴を調べるときの値（代表値）について理解を深めておくことが大切です。本時のように、代表者を決めるような問題場面の場合、与えられたデータの優れた数値だけに注目したり、＜資料＞の表の数値の優劣を多数決的に判断したりする子供の反応が予想されます。その判断の仕方は間違ってはいないのですが、データを短絡的に捉えて安易に結論を出してしまうことは、本時で望む子供の姿とは言えません。

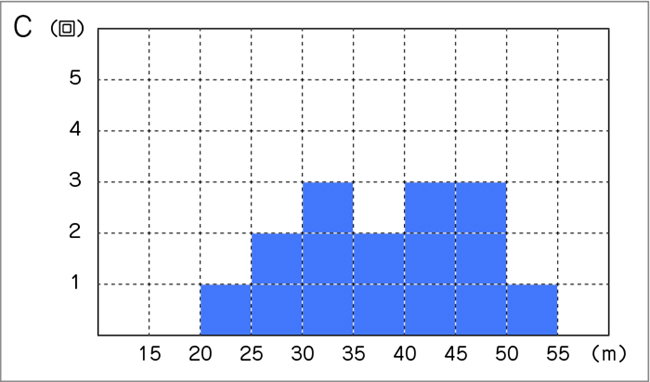
本時の望む子供の姿は、例えば、Ａさんのムラのある結果について、「⑬18ｍは失敗したのかもしれないから、その数値を除いて平均値を出したほうがＡさんの本当の実力が分かるかもしれない」と考えたり、＜資料＞の数値ではやや劣るＣさんの結果について、｢ドットプロットや折れ線グラフに表すと、練習後半になるにつれて結果が伸びてきたことが分かるから、大会本番ではよい記録が望めそうだ」と考えたりする姿です。データが示す数値を自分なりにどのように捉え、どの方法で表し、どの結論に導くかにこだわって話し合う学習展開によって、主体的・対話的な学びが生まれるでしょう。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

それぞれの資料を詳しく分析して、みなさんは誰を代表者にすればよいと思いますか。

私は、Ｂさんを代表にすればいいと思います。私は、ヒストグラムを基に考えました。みなさん、ヒストグラムの形に注目してください。ＡさんやＣさんのヒストグラムは横に広がっていて、よい結果のときもあれば悪い結果のときもあることを表しています。でも、Ｂさんのヒストグラムは集まっていて、安定してよい結果が出せることを表しています。悪い結果が出ず、常によい結果が出せるＢさんが代表にふさわしいと思います。

その考えも分かるのだけど、僕はＢさんの最大値が50ｍに達していないところが引っかかります。いくら安定していても、50ｍも飛んでいなかったら、他のクラスに負けてしまうと思います。クラスの代表者には絶対に勝ってほしいです。

僕もＡさんを代表にすれば勝てると思います。＜資料＞のなかの一番の数値に色を塗ってみました。すると、３つも一番を取っているＡさんは３人のなかで一番優れていることが分かります。

でも、これだけではないんです。僕は、前に習ったドットプロットにして見たら、すごいことが分かりました。３人のドットプロットを並べて、40ｍ以上飛んだ回数を数えてみると、Ｂさんは６回、Ｃさんは７回なのに比べて、Ａさんはなんと９回も飛んでいます。こんなにたくさん飛ばせるＡさんを代表にすれば、絶対に勝てると思います。

なるほど。Ａさんを代表にする理由が２つもあるなら、Ａさんを代表にしたいなぁ。

私はムラのあるＡさんには安心して任せられないなぁ。でも、安定感のあるＢさんだと勝つことは難しいかもしれないし……。

みなさんは、ＡさんとＢさんのどちらかで悩んでいるようですが、Ｃさんは代表者になる可能性はありませんか。

絶対にありません。表のなかでも一番は１つだけだし、ヒストグラムもＡさんの次にムラがあるから、Ｃさんが代表になっても勝てる可能性は低すぎます。

〈Ｃ１さん〉待ってください。私は、代表者にＣさんを選びたいと思っています。

どうして。よい結果が少ないＣさんを選んでも勝てっこないよ。

〈Ｃ１さん〉私の理由を聞いてくれますか。私もドットプロットで考え始めたのだけど、注目したのは「○回目」なんです。

〈Ｃ１さん〉Ｃさんは９回目以降、ずっと40m以上飛ばし続けていることに気が付きました。これをもっと分かりやすくするために、３人の練習結果を折れ線グラフで表してみました。すると、Ｃさんは練習を重ねるごとに成長していることが分かりました。表の数値では低いものが多かったかもしれませんが、大会本番に向けて調子が上がっているＣさんは一番期待できると思いませんか。

本当だ。折れ線グラフだと、Ｃさんがぐんぐん力を付けている様子がよく分かるね。

それにＢさんも意外と結果にムラがあることが分かるよ。ヒストグラムでは安定して見えていたのに、グラフの表し方でこんなに違って見えるなんて不思議だなぁ。

ＡさんとＢさん以外に、Ｃさんも代表者の候補に挙がってきましたね。みなさん、代表者は誰にしましょうか。

う～ん……。誰にしよう。迷うなぁ。

先生、まだ大会まで３日あるんですよね。この３日間、もう少し様子を見ることはできませんか。

どうしてそう思うのですか。

３人とも実力があることが分かっているのだから、残り３日でさらに記録を伸ばす可能性が３人ともあると思うんです。

残り３日間のデータも加えて、もう一度分析し直したらそれぞれの数値やグラフが変化するかもしれないからね。

この段階では代表者を決められないということですね。そういう結論もありだと思います。他のみなさんは、どうですか。与えられたデータをさらにくわしく見直すことで、より深い考えで結論を見いだせるかもしれませんね。

僕も、このあとの３日間のデータを付け足して考えてみたいです。

私もです。そうすれば、より多くのみんなが納得できる結論になると思います。

では、代表者を決めるのはもう少し待つとして、３人のここまでの記録の特徴を整理しておきましょう。それぞれどのような特徴があり、それはどのデータから分かったのでしょう。

Ａさんは３人のなかで一番遠くまで飛ばしていました。表やドットプロットから分かります。その反面、一番飛ばなかった記録も出ていて、記録にムラがあるのが特徴でした。ヒストグラムの広がりや折れ線グラフでも、それが表れていました。

Ｂさんは、同じくらいの記録が安定して出せるのが特徴でした。ヒストグラムの広がりが狭く、最頻値が一番大きいことからも安定感があることが分かりました。

Ｃさんは、練習の後半に記録を伸ばしてきたのが特徴でした。折れ線グラフにすると、ぐんぐん記録が伸びている様子がよく分かりました。45ｍ以上飛ばしている記録の割合の多さからも、本番でよい記録が出せそうな予感が一番します。

データをくわしく分析して、３人の記録の特徴を押さえることができましたね。

学習のまとめ

＜３人の特徴＞

３人のデータには、それぞれによいところがある。
平均だけで、簡単には決められない。
誰を代表にするかという考えを説明したり聞いたりするときは、データのどこを理由にしているのかをはっきりさせることが大切だと思う。
データをいろんな点からくわしく見たり、さらにデータを付け足したりして調べていくと、代表を決めるという問題を解決することができる。

多角的にデータを見ていくことで、よりよい結論を出していくことができる。
データを使うと、考えの理由を説明しやすくなる。

評価問題

15日分のデータをみんなでよく調べました。でも、みんなを納得させることのできる結論にまではまだなっていません。この先、どのようなことをすれば、みんなに納得してもらえる結論になると思いますか。あなたの考えを書きましょう。

子供に期待する解答の具体例

もう一度、平均値や最頻値などを計算し直して、計算ミスがないか確かめたい。
データを１つ１つ見直して、最低値や最高値の測定にミスがなかったか、確かめたい。
（データを再吟味して、より信頼性と妥当性のある結論にすることを考えている）
後半の５日間だけを取り出して、結論を考えてみたい。
（練習効果や記録の伸びに着目して、大会で期待できる数値を考えようとしている）

本時の評価規準を達成した子供の具体の姿

データの特徴や傾向に着目して、代表値を決め問題に対する結論を判断するためのよりよい方法を考えようとしている。

感想例

簡単に数値だけで判断してはいけないことが分かりました。数値を通してＡさんたちのことを知ろうとすることで、データをくわしく分析することができると思いました。
データの分析で大切なことは、たくさんのデータを総合的に見たり、データの一部だけに注目して考えたりするなどの工夫をしたりすることだと考えました。
大きな数値に目が行きがちだったけれど、データを、くわしく見ることでＡさんたちの成長の様子を見ることができました。今日習った見方をすることで努力する姿が伝わるので、データを分析することはとても大切だと思いました。
データをくわしく見ることで、資料のもつ本当の情報に触れることができた。この見方は、学校生活の様々な場面でも役に立つと思うので生かしていきたい。
データの一部に注目したり、本番に向けて調子を上げている人を見付けたりするなど、僕にはない見方をしている人がいて参考になった。データを広く多角的に見ることの重要性を感じました。