小６算数「分数×分数」指導アイデア《乗数の分子が１のときの分数×分数の計算の仕方を考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.08.15

単元の展開

第１時（本時）乗数の分子が１のときの（分数）×（分数）の計算の仕方を考える。
▼
第２時　乗数の分子が１以外のときの（分数）×（分数）の計算の仕方を考える。
▼　　　《乗数の分子が１以外のときの分数×分数の計算》
第３時　乗数が仮分数の計算の仕方を考える。
▼
第４時　帯分数や整数が入った分数のかけ算の計算の仕方を考える。
▼
第５時　（小数）×（分数）、（分数）×（小数）の計算の仕方を考える。
▼　　　《小数と分数が混じったかけ算の仕方》
第６時　１より小さい分数を掛けると、積は被乗数より小さくなることを理解する。
▼
第７時　（分数）×（分数）×（分数）の計算の仕方を考える。
▼
第８時　長さが分数で表されている長方形の面積と直方体の体積を求める。
▼
第９時　交換法則や結合法則、分配法則が、分数の計算にも適用できるか考える。
▼
第10時　積が１になる乗数を見付け、被乗数の乗数との間のきまりを見付ける。
▼
第11時　練習問題を解き、学習内容の理解を深める。

本時のねらい

分数×分数（分子が１）の計算について、図や数直線、計算のきまりなどを基にして多面的に考える。

評価規準

分子が１の分数の意味と表現に着目し、分数×分数（分子が１）の計算の意味や計算の仕方を、図や数直線、計算のきまりなどを基にして多面的に捉え考えている。（思考･判断･表現）

本時の展開

１dLで[MATH]\(\frac{4}{5}\)[/MATH]㎡ぬれるペンキがあります。このペンキ[MATH]\(\frac{1}{3}\)[/MATH]dLでは、何㎡ぬれますか。

ペンキ[MATH]\(\frac{1}{3}\)[/MATH]dLでは、何㎡塗ることができるかを求める式は、どんな式になりますか。

もし２dLだったら、[MATH]\(\frac{4}{5}\)[/MATH]㎡の２倍の面積を塗れるから、式は、[MATH]\(\frac{4}{5}\)[/MATH]×２です。

３dLだったら、[MATH]\(\frac{4}{5}\)[/MATH]の３倍の面積を塗れるから、[MATH]\(\frac{4}{5}\)[/MATH]×３。つまり、どちらも、（１dLで塗れる面積）×（ペンキの量）＝（塗れる面積）になります。

だから、[MATH]\(\frac{1}{3}\)[/MATH]dLだったら、式は「[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]」になるね。

数直線図をかいて確認しよう。

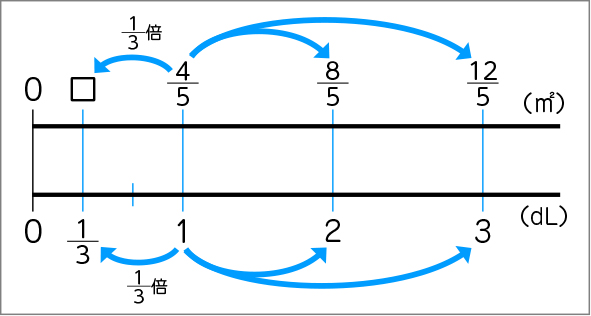
数直線図からも、式は[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]になるね。

でも、掛ける数が分数の計算は初めてだよね。整数だったら、分子に掛ければ計算できたけど。

[MATH]\(\frac{1}{3}\)[/MATH]を掛けるというのは、どういうことになるのかな。

今日は、みんなで、[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]について考えて、分数に分数を掛ける計算の仕方を考えましょう。

分数×分数（分子が１）の計算の仕方を考えよう。
↓
（そのために）[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]の計算の仕方を考えよう。

見通し

面積図や数直線図を使って、考えよう。（方法の見通し）

計算のきまりを使って、既習の計算を生かして計算の仕方を考えよう。（方法の見通し）

１より小さい[MATH]\(\frac{1}{3}\)[/MATH]を掛けるので、[MATH]\(\frac{4}{5}\)[/MATH]より小さくなるだろう。（結果の大きさの見通し）

自力解決の様子

A　つまずいている子
・[MATH]\(\frac{1}{3}\)[/MATH]を掛けるというイメージをもつことができない。
・面積図を使って考えるために縦に３つに分ける方法を教えてもらうが、それがどのような意味をもっているのか困っている。

Ｂ　素朴に解いている子
・[MATH]\(\frac{1}{3}\)[/MATH]を掛けるということは、[MATH]\(\frac{1}{3}\)[/MATH]倍にすることだと考えている。
・[MATH]\(\frac{1}{3}\)[/MATH]倍をすることは、３で割ることと同じだと理解している。
・求める積は掛けられる数の[MATH]\(\frac{1}{3}\)[/MATH]の大きさになりそうだと思っている。
・面積図を使って、15に分けたうちの４つ分になるから、[MATH]\(\frac{4}{15}\)[/MATH]と答えを導き出している。

Ｃ　ねらい通り解いている子
・面積図を用いて、[MATH]\(\frac{1}{3}\)[/MATH]を掛けるということは、[MATH]\(\frac{1}{3}\)[/MATH]の大きさになるということを基にして、図から[MATH]\(\frac{4}{15}\)[/MATH]と答えを導き出している。
・面積図と式を対応させて、分母どうし、分子どうしを掛けることに気付いている。
・分数×整数の計算に直して答えを確かめている。（掛ける数の[MATH]\(\frac{1}{3}\)[/MATH]を３倍して整数の１にしてから求めて、それを３で割る）
・積の[MATH]\(\frac{4}{15}\)[/MATH]の意味について考えている。（[MATH]\(\frac{1}{15}\)[/MATH]の４つ分、[MATH]\(\frac{4}{5}\)[/MATH]の３等分）

学び合いの計画

本単元では、分数を掛ける意味を面積図や数直線図などに表し、分数×分数の計算の仕方とつなげて考えていくことが大切です。そのために、分数×整数や分数÷整数、そして計算のきまりなど、既習事項を活用しながら学び合いを進めていきます。掛ける数が１になる分数のかけ算の仕方を理解することが土台となり、図や計算のきまりを使って、新しい計算を工夫しながら考えていくことの楽しさも感じることができるでしょう。

まず、分数で掛けることの意味を考えるために、数直線図や面積図に[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]について表しましょう。面積図に分数を掛けることをどのように表すかということはとても難しいです。その際には、みんなで共有できる数直線図や面積図があると、式の意味や計算の仕方の理解につながるでしょう。また、計算のきまりを用いて、計算の仕方を考えていくことの楽しさを感じるためには、式とポイントを分かりやすく板書に表したり、違う数でも追体験できるようにしたりするとよいでしょう。

授業の終末には、１時間で学んだことを自分の言葉でふり返ることが、次の時間の学習へとつながります。ふり返りについても、子供どうしで共有し合うと、算数の楽しさや多様な考えに気付くことができるでしょう。