｢この式はこうなっている｣「この式にも共通点がある」と帰納的に考えさせる 【全国優秀教師にインタビュー！ コレが私の授業づくり！ 第１回】

このリレー連載企画では、全国の優秀教師の方々が、｢この授業こそ、私の授業づくりを具現化したものだ」と考える授業を通して、そこに表れている、授業づくりの考え方を紹介していく企画です。多くの先生方にお読みいただき、授業づくりの参考にしていただければと思います。
初回は、宮崎県のスーパーティーチャー（小学校・算数）である、中西英指導教諭の算数の授業を紹介していきます。

式を整理する活動を通して、子供たちが規則性に気付く

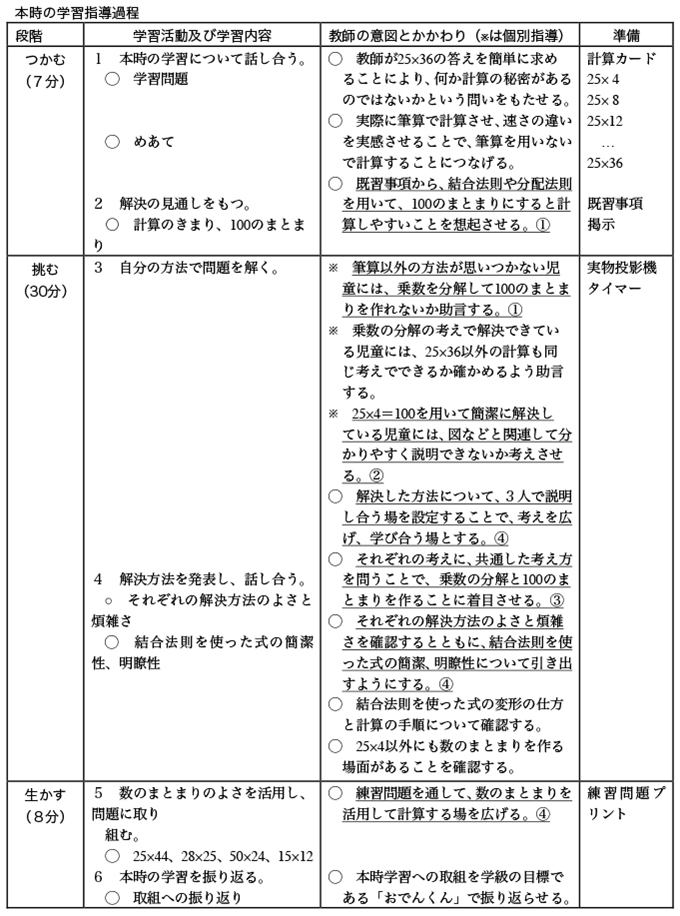
最初に紹介するのは、中西先生が以前、算数科の九州大会で発表を行った、４年生の「式と計算のきまり」の単元の授業です。この授業は全10時間の単元の中の７時間目。四則計算のきまりや交換法則、分配法則などについて学習した後、子供たちがその法則などを使って、25×36の計算を工夫して行うことが中心の問題となる授業です。まず中西先生は、この授業を工夫した理由を次のように説明します。

｢この単元はなかなか定着が良くないのです。教科書では、この授業で取り上げた、25×36だけでなく、45＋92＋８、99×56など３問を１時間で扱うことになっており、子供にとってはハードルが高いものです。そのため教科書では、穴埋め式で当てはめていく形になっていますが、それでは十分に思考が働かないし、あまり定着も高まりません。そこで、子供たちが簡単な並べ替えをする活動を通して、自然と規則性に気付いていくような授業を考えました」

では、どんな授業なのか、紹介していただくことにしましょう（下の指導案参照）。

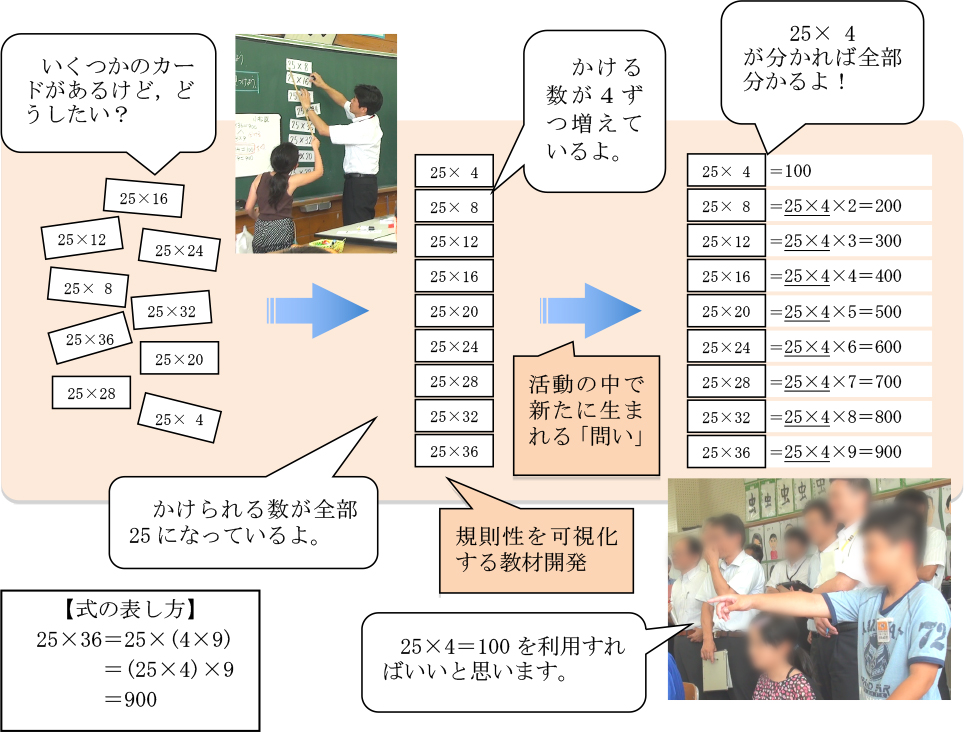
｢この授業では、最初に私が25×36という問題を提示し、答えはいくらか問います。すると、みんな工夫して計算を簡単にするのではなく、実際にひっ算で計算して、900という答えを出します。次に、袋の中に準備しておいた他のかけ算の式を、１人の子供に引かせ、この授業のときには25×12という式が出てきたのですが、数名の子供はすぐに『分かる』と言います。そこで､『どうして、そんなに速くできるの？』ということを問題にしたのです。

ここで、即座に計算ができた子供に、25×36を工夫した考え方を説明してもらうと､『私は25が何個で100ができるか考えました。２個だと50、３個だと75だけど、４個だと100になります。だから36の中に４が何個あるかと考え、９個あるので、25×36は900になります』と説明します。この説明は、私たち大人（参観者の教員）には分かるのですが、子供たちの反応は（事前に想定していた通り）今一つボヤッとした感じ。小学４年の子供たちの多くにとっては、この言葉による説明は分かりにくいのです。

そこで、私が袋の中に用意をしておいた、25×（４の倍数）の式をランダムに引いて、黒板にバラバラに貼っていきます。そうして、このままでは分かりにくいという子供の意見を受け､『式を整理したほうがいい』と挙手をした子供たちの中から１名を指名して、整理させていきます」

実際の授業動画を見ると、あまり算数が得意ではなさそうな様子の子供が、最初は25にかける数の大きさで漠然と黒板の上下に分けて整理をし始めるのですが、途中から規則性に気付いた様子で、次第に整理時間が速まり、25×４、25×８、25×12…25×32、25×36と、黒板の上から下に式を整理していきます。

｢並べ替える活動を通して、整理をしている子供だけでなく、教室の子供たち全員も規則性を共有していくのです。そういう学習過程を経ていくことで､『かける数が４ずつ増えている』『25×４が分かれば、全部の答えが分かります』『25×４は100ですよね。だから、25×８＝200…25×36＝900になります』と、子供たちが口々に説明していきました（資料参照）」

最後の子供の説明は、最初に25×36を速く計算した子供の考え方の説明とあまり異なるものではありません。しかし、式を整理する活動を通して、教室の大半の子供たちが規則性に気付くことで、同様の説明がスムーズに受け入れられているわけです。

（資料）

教科書ベースでの授業は、数学的な楽しさは伝わりにくい

｢このように、整理する活動（過程）を共有することで『25×４を基にすると計算が簡単にできる』ということを、全員に浸透させていくようなイメージですね。

教科書ベースで授業を行うと、最初にご説明した通り、穴埋め式になっていて、式をどう変形するかという点に特化しているため、算数・数学的なおもしろさ、楽しさは伝わりにくいと思います。既習の法則性、規則性を演繹的に使うだけでなく､『この式はこうなっている』『この式にも共通点がある』と帰納的に考えて、子供たち自身が規則性を発見していくような学習もあったほうが楽しいと思うのです」

ちなみに、この授業では子供たちが式の規則性に気付き、工夫して速く計算ができるようになった後、｢25×４＝100などのまとまりにして計算すると簡単にできる」と子供たちが学習をまとめます。その上で、気付いた「数のまとまりの良さ」を活用して計算を工夫する問題に取り組んでいくのです。その活用問題も、最初は25×44と４のまとまりが２桁になるもので、次は28×25で、かける数とかけられる数が逆になったもの、さらに50×24と50を２つずつのまとまりで考えるもの、さらに15×12と異なる規則性を見いだすものとなっています。

※

今回は、中西先生の授業づくりの考え方を象徴する授業を紹介していきました。次回は、このような授業づくりの裏にある、中西先生の授業づくりの考え方について、ご紹介します。

【全国優秀教師にインタビュー！　コレが私の授業づくり！】次回は、３月１日公開予定です。

執筆／教育ジャーナリスト・矢ノ浦勝之