小４算数「式と計算」指導アイデア《分配法則についての理解》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2023.12.12

単元の展開

第１時　２つの式で表される場面について、１つの式に表す方法を（　　）を用いて考え、説明する。
▼
第２時　四則計算の式の表し方や計算順序を理解する。
▼
第３時　より複雑な四則計算の式の表し方や計算順序を理解する。
▼
第４時　ドットの並び方やまとまりに着目し、ドットの数の求め方を、１つの式にまとめたり、図や式から考え方を読み取ったりしながら、説明する。
▼
第５時（本時）数や式の形に着目して、分配法則について理解し、それが適応できるか判断し、その計算方法を説明する。
▼
第６時　数や式の形に着目して、交換法則や結合法則について理解し、それが適応できるか判断し、その計算方法を説明する。
▼
第７時　被乗数と乗数、積に着目し、乗法の性質を理解する。
▼
第８時　学習内容を確認し、数学的な見方・考え方をふり返る。

本時のねらい

数や式の形に着目して、より効率的に計算するために、分配法則について理解し、それが適応できるか判断し、その計算方法を説明する。

評価規準

数や式の形に着目し、分配法則が適応できるか考え、その計算方法を説明することができる。

本時の展開

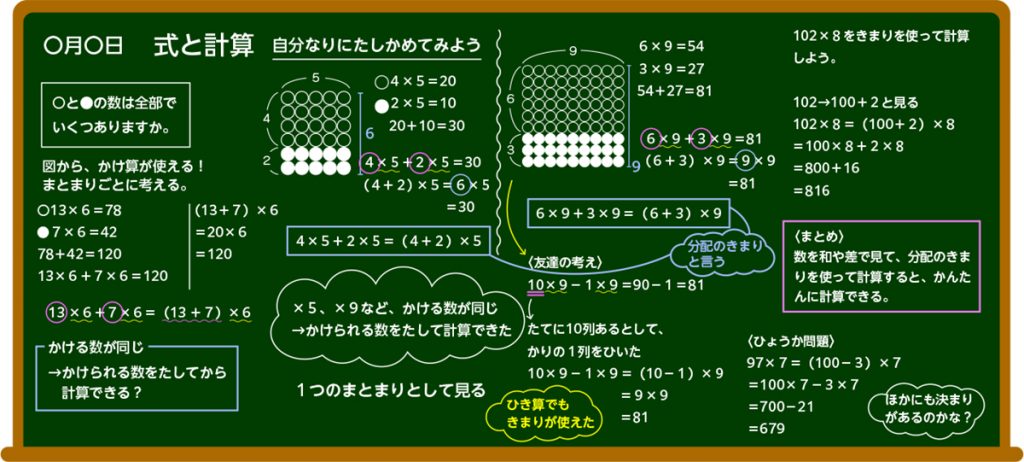
図のなかの、〇と●の数は全部でいくつありますか。
　

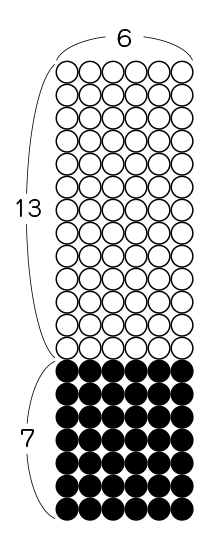
この図のなかの、〇と●の数は全部でいくつありますか。

図を見ると、かけ算が使えそう。

なぜかけ算が使えそうなのですか。

色ごとにまとまりがあるからです。

そうですね、では、かけ算を使って、〇と●の数を数えてみましょう。

※自力解決をする。

全部でいくつになりましたか。

120個です。

なぜ、120個と分かったのですか。

13×６＋７×６で求めることができました。

図で言うと、どこのことか分かりますか。

13×６が〇の数、７×６が●の数です。

私は違う式で求めました。（13＋７）×６で求めました。

図を使って説明できますか。

さっきの13×６＋７×６の２つのまとまりは、横の〇の数が一緒になっています。縦の数だけ違うので、縦を１つにまとめて、13＋７にして考えました。

縦をまとめたほうが簡単かもしれないね。

２つの式は、同じ答えになるんだね。

そうですね。２つの式をつなげてみましょう。

13×６＋７×６＝（13＋７）×６

×６のように、掛ける数が同じだった場合、掛けられる数を最初に足してもいいのかもしれないね。

そうか。でも、偶然かもよ。

ほかの問題で確かめてみようよ。

では、自分で問題を考えて解いてみましょう。掛ける数が同じだった場合、変えられる数どうしを足してから計算してもいいかという見通しをもって、今日の学習を進めましょう。

×６のように、掛ける数が同じ場合、掛けられる数を最初に足して計算してもよいか考えよう。

見通し

掛ける数と掛けられる数に注目すると､（　）を使った式にできそうだな。（方法の見通し）

共通のまとまりを見付けるといいかもしれないな。（方法の見通し）

掛ける数が同じ場合、掛けられる数を１つにまとめられそうだな。（結果の見通し）

自力解決の様子

A　つまずいている子
分配法則の考え方がわからず、やり方も計算の答えも間違っている。

Ｂ　素朴に解いている子
分配法則を仕組みの通りに計算している。

Ｃ　ねらい通り解いている子
分配法則の仕組みを理解し、問題を見て、その法則が適応できるか考え、どうしたらより効率よく計算できるか考えている。

学び合いの計画

分配法則を使って計算するだけでなく、問題を見て、この問題では法則を使うほうがよいのか、使わずに計算するほうがよいのかを判断しようとする子を育てましょう。

そのために、被乗数や乗数に着目し、被乗数がどのような数なのかを、図で言うとどこのことなのかを考えさせます。それを共有していくことで、数を豊かに見る視点も養われます。

数をなぜそのように見たのか、なぜ分配法則が適応できるのかなどを説明できるようにしましょう。

説明の際は、ICT機器を使うなど、学び合いのなかで、より数の見方が豊かになるようにします。その見方が養われることによって、分配法則だけでなく、後に学習する交換法則や結合法則についての理解のしやすさにつながっていきます。

数を和や差で見たり、分解して考えたりすることで、計算をより効果的に行うようにします。そのよさを実感し、次の学びにつなげていきましょう。

また、自分で考えた図で分配法則が成り立つかどうかを考えることで、帰納的な思考が養われるだけでなく、「この場合はどうか」など、次の問いも生まれ、意欲につながります。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

※Ｃ１、Ｃ２、Ｃ３のそれぞれが発表をする。

Ｃ１
この図で考えました。
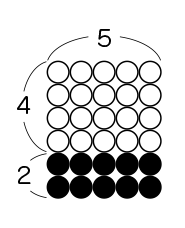
４×５＝20 ２×５＝10
20＋10になり、全部で30になります。
次に、縦を（４＋２）として考えます。
（４＋２）×５なので、６×５で30になります。
　

Ｃ２
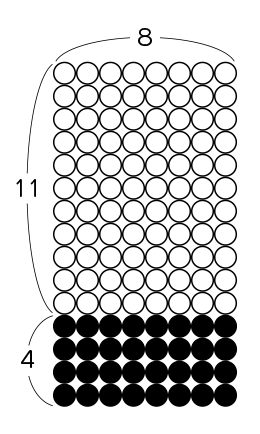
この図で考えました。
11×８＝88　　４×８＝32
88＋32になり、全部で120になります。
次に、縦を（11＋４）として考えます。
（11＋４）×８なので、15×８で120になります。
　

Ｃ３
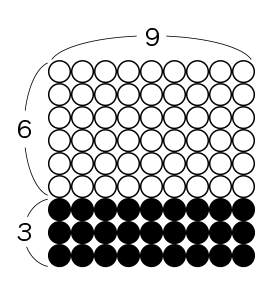
この図で考えました。
６×９＝54 ３×９＝27
54＋27になり、全部で81になります。
次に、縦を（６＋３）として考えます。
（６＋３）×９なので、９×９で81になります。
　

３つを見比べて、気付いたことや考えたことはありますか。

それぞれの考えを見ると、見通しの通り、答えが同じになるので、掛けられる数を足してから計算してもいいと思います。

図を見てもわかると思います。Ｃ１さんの考えを見ると、縦に６のまとまりが５列あることと一緒であることがわかります。

だから６×５で求められるんだね。

Ｃ２さんの図でも、Ｃ３さんの図でも、同じことが言えるね。

ということは、最初に立てた予想は間違ってなさそうですか。

間違っていないと思います。

掛ける数が同じだった場合、掛けられる数を最初に足してもいいと思います。

私はＣ３さんの図を見て、別の求め方もあると思いました。　

どんな求め方ですか。

縦の個数をまとまりで見ることができるなら、６＋３ではなくて10－１でもできそうです。

10－１というのは、どういうことですか。　

Ｃ３さんの図にもう一列●があることにすると、縦に10のまとまりができます。そうすると10×９で90個の◯と●があります。そこから付け足した１列の●９個分を引きます。

なるほど。式で表すとどうなりますか。

10×９―１×９になります。

掛ける数の×９が同じだ。

そしたら、これも（　）を使った式にできるかもしれないね。

先に掛けられる数を引いてから計算できるんじゃないかな。

10×９―１×９＝（10―１）×９になるね。

（10―１）×９は９×９のことだから、◯と●は全部で81個あるね。

（６＋３）×９で求めた数と一緒だね。

掛ける数が一緒のときは、最初に足したり引いたりしてもよさそうだね。

そうですね。このような計算のきまりを、分配のきまりと言います。このきまりを使って、今度は102×9を工夫して計算できますか。　

できそう！　102を（100＋２）に分けたら計算しやすそう。

今度は分けるんだね。

そうすると、どのように求められますか。

102×９＝（100＋２）×９になります。これは100×９＋２×９と同じになります。なので、900＋18で918が答えになります。

98×９のときはどうなるかわかりますか。

分かります。98を100―２と見ればいいです。

数を和や差で見ることができていますね。では、自分で計算のきまりが使えそうな問題を考えてみましょう。タブレットでみんなで共有しましょう。

数を和や差で見て、分配のきまりを使って計算すると、簡単に計算することができました。

評価問題

97×７の計算を、きまりを使って説明しよう。

子供に期待する解答の具体例

97×７をそのまま計算するよりも、暗算がしやすい数に置き換えるとよいと考えました。97を100－３とします｡（100－３）×７となって、ここにきまりを使うと100×７―３×７と同じになります。700―21＝679が答えになります。

本時の評価規準を達成した子供の具体の姿

掛けられる数を差で見て、分配のきまりを使って、そのまま計算するよりも効率的であることを説明している。

感想例

数を和や差を使って計算しやすい数にしてから、分配のきまりを使うと、今までの計算がもっと簡単にできるようになりました。ほかにも簡単になる計算のきまりがあるのか考えてみたいです。

ワークシート（ダウンロード可）

ダウンロードはこちら＞＞

板書例

イラスト／横井智美

【関連記事】

1人1台端末時代の｢教科指導のヒントとアイデア｣シリーズはこちら！

>>もっと見る

小学館IDをお持ちの方はこちら

初めてご利用の方