小六算数 「つまり」や「だったら」が生まれる授業とは
凄腕実践者・前田正秀先生が、「子供自身のリフレクション」により深い学びが生まれる条件について考察。さらに、算数の授業実践例の中で、実際に機能させるための様々な工夫や仕掛けを具体的に提案します。
執筆/富山県公立小学校・前田正秀
富山大学附属小学校で10年間勤務後、現職。「あれ?」「おや!」と心が揺さぶられる授業を目指しています。

目次
「だったら」が生まれる授業を!
アクティブな問題解決型授業。その終末に、子供のどんな姿を期待すればよいでしょうか。私は、子供から「だったら・・・」という言葉が生まれてきてほしいと願っています。学習した内容をまとめ、そこで学びを閉じてしまうのではなく、新たな問いが生まれてほしいと思うのです。
2年生で「三角形と四角形」の学習をした時のことです。三角形と四角形の定義をまとめていると、ある子供がふと「三角形と四角形があるんだったら、五角形や六角形もあるんじゃないの」とつぶやきました。そこで、「まだ習わないけど、実は五角形や六角形もあるんだよ」と伝え、黒板に五角形や六角形を描いてみせました。
すると、他の子も「だったら、七角形や八角形もあるんじゃないの」と続き、さらには「百角形も!」「千角形も!」と言う子も出てきました。
そんな中、ある子が「でも、一角形や二角形はないよね」と、つぶやきました。なるほど、大人からすれば当たり前のことなのですが、そんなことに気付くとは面白い発想です。
そう思って感心していると、別の子が「先生、一角形もあるよ」という声を上げたので、驚きました。その子は、「しずくの形だよ」と言いながら黒板に次のような形を描いたのです。

確かに角が一つの形です。一角形の発見に、クラスがざわめきました。
私は「だったら、二角形は猫の形だね」「三角形は、チューリップの形だね」と言い、次のような形を黒板に描きました。
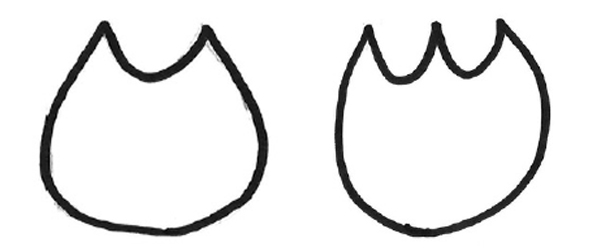
すると、子供たちは「あれ?」という表情になりました。「そんなの三角形って言わないよ」と言うのです。そこで、どうしてチューリップの形は三角形と言えないのか、その理由を話し合いました。子供たちは「角があるだけじゃ駄目。3本の直線が要るよ!」「曲がった線じゃ駄目。直線で囲まれないと!」などと説明していきました。
三角形の定義は、「3本の直線で囲まれた形」です。子供たちは、「だったら・・・」と考えていく中で、分かったつもりになっていた三角形の定義を、もう一度見つめ直し、理解を深めたのです。
強い「なるほど」が、「だったら」を生む!
東京書籍の六年の教科書には、「不思議な輪の変身」という教材が紹介されています。二つの輪っかを垂直に貼り合わせて、輪っかの真ん中を切って開くというものです。

開くと、なんと正方形になるのです。こうした教材を「へえ、そうなんだ」で終わらせたくありません。「だったら、斜めに貼り合わせたら、ひし形になるはず」「だったら、違う長さの輪っかを貼り合わせたら、長方形になるはず」「だったら、輪っかを3個貼り合わせたら、どうなるんだろう」と、問いを発展させてほしいのです。
では、「だったら」を生み出すには、どうすればよいのでしょうか。
単に、教師が切って開いて見せただけでは、子供から「だったら」が生まれてはこないでしょう。「だったら」を生み出すには、強い「なるほど」が必要です。切って開いた形を予想し、その理由を話し合い、仕組みを理解し、「なるほど」と心が動かされるからこそ、「だったら」が生まれてくるのです。
最初のうち、開いた形は予想もつきません。しかし、一つ目の輪っかを切って開いた段階で、だんだん予想がついてきます。

子供からは「きっと四角形になるよ」といった声が上がることでしょう。さらに、「四角形は四角形でも、長方形になるよ。だって、垂直に貼り合わせたんだから、四つの角は直角になるはず」「長方形じゃなくて、正方形じゃないかな。二つの同じ輪っかを貼り合わせたんだから、四つの辺の長さが同じになるはず」といった考えも出てくるでしょう。
こうした話合いを経た上で、切って開けば、「なるほど」という思いが強くなります。そして、「なるほど、垂直に貼り合わせたから、四つの角が直角になったんだ。だったら、垂直じゃなかったら・・・」「なるほど、同じ輪っかを貼り合わせたから、四辺の長さが等しくなったんだ。だったら、違う大きさの輪っかだったら・・・」と、「だったら」が生まれてくるのです。

